สมมาตรคืออะไร?

ในเรขาคณิตวัตถุแสดงความสมมาตรหากดูเหมือนกันหลังจากการเปลี่ยนแปลงเช่นการสะท้อนหรือการหมุน Symmetry เป็นหลักการทางคณิตศาสตร์พื้นฐานที่อยู่เบื้องหลังรูปแบบทั้งหมดและมีความสำคัญในศิลปะ (ใช้ในสถาปัตยกรรม, เครื่องปั้นดินเผา, การสร้างควิลท์และพรม), คณิตศาสตร์ (เกี่ยวข้องกับเรขาคณิต, ทฤษฎีกลุ่มและพีชคณิตเชิงเส้น), ชีววิทยาสมมาตรสอดคล้องกับปริมาณที่อนุรักษ์ไว้- คำว่า "สมมาตร" เป็นอนุพันธ์ละตินในศตวรรษที่ 16 จากคำภาษากรีกสำหรับ "ร่วมกัน" (ซิงค์-) และ "วัด" (รถไฟใต้ดิน-

ประเภทของความสมมาตร

สะท้อนแสง

โดยทั่วไปการใช้งานสมมาตรส่วนใหญ่มักหมายถึงกระจกเงาหรือสะท้อนแสงสมมาตร; นั่นคือเส้น (ใน 2-D) หรือระนาบ (ใน 3-D) สามารถวาดผ่านวัตถุที่สองครึ่งเป็นภาพสะท้อนของกันและกัน สามเหลี่ยมหน้าจั่วและใบหน้าของมนุษย์เป็นตัวอย่าง ในทางคณิตศาสตร์วัตถุที่แสดงความสมมาตรของกระจกถูกกล่าวว่าเป็น

ในชีววิทยาความสมมาตรแบบสะท้อนแสงมักจะเรียกว่าสมมาตรทวิภาคีตามที่พบในสัตว์เลี้ยงลูกด้วยนมสัตว์เลื้อยคลานนกและปลา

เกี่ยวกับการหมุน

อีกรูปแบบหนึ่งของความสมมาตรที่พบในชีววิทยาคือความสมมาตรของรัศมี- พบในดอกไม้และสัตว์ทะเลมากมายเช่นดอกไม้ทะเลดาวทะเลและแมงกะพรุน ในทางคณิตศาสตร์วัตถุดังกล่าวอธิบายว่าเป็นการจัดแสดงเกี่ยวกับการหมุนสมมาตรสำหรับการเป็น“ ค่าคงที่ภายใต้การหมุน” วัตถุดังกล่าวมีจุด (ใน 2-D) หรือแกน (ใน 3-D) เกี่ยวกับวัตถุที่สามารถหมุนได้จำนวนมากและยังคงไม่เปลี่ยนแปลง

การแปล

หากจินตนาการว่าจะขยายไปถึงอินฟินิตี้ในทุกทิศทางรูปแบบ 2 มิติหรือ 3 มิติสามารถแสดงได้การแปลสมมาตรสำหรับการเป็น“ ค่าคงที่ภายใต้การแปล” ทั้งหมดTessellationsโรงยิมป่าหลายแห่งและรูปแบบส่วนใหญ่ที่พบในพรมและวอลล์เปเปอร์แสดงความสมมาตรการแปล

รูปแบบอื่น ๆ ของสมมาตร

ในขณะที่มีตัวอย่างของวัตถุที่แสดงความสมมาตรมากกว่าหนึ่งประเภท (เช่นดาวหกแฉกแสดงการสะท้อนหกบรรทัดและจุดหมุน 6 เท่า) มีวัตถุและรูปแบบบางอย่างที่ไม่เปลี่ยนแปลงภายใต้การแปลงสองครั้งทำในเวลาเดียวกัน-

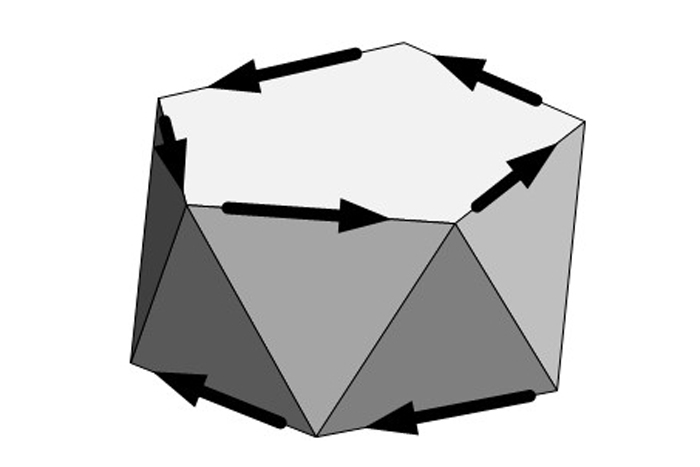
การหมุนที่ไม่เหมาะสม =การสะท้อน + การหมุน

antiprism pentagonal ที่มีขอบทิศทางเป็นค่าคงที่ภายใต้การหมุนที่ไม่เหมาะสม (ในตัวอย่างด้านบนการหมุนโดยสิบของวงกลมและสะท้อนข้ามระนาบแนวนอน)

การสะท้อนแสง =การแปล + การสะท้อนกลับ

รูปแบบรอยเท้าเช่นตัวอย่างข้างต้นหากขยายไปถึงอินฟินิตี้ในทิศทางใดทิศทางหนึ่งจะไม่เปลี่ยนแปลงภายใต้การสะท้อนแสง (การแปลรวมกับการสะท้อน)

สกรูหมุน =การแปล + การหมุน

เกลียวที่ทำจากจัตุรมการหมุน 131.8 องศา-

การจัดหมวดหมู่วัตถุและรูปแบบ

นักคณิตศาสตร์และนักตกผลึกจัดหมวดหมู่ความสมมาตรของวัตถุหรือลวดลายตามความหลากหลายของวิธีที่สามารถเปลี่ยนได้และยังคงไม่เปลี่ยนแปลง วัตถุ 2-D หรือ 3-D ได้รับการกำหนด "กลุ่มจุด" เพื่อระบุวิธีการทั้งหมดที่สามารถคงอยู่ภายใต้การสะท้อนและการหมุน (และใน 3 มิติการหมุนที่ไม่เหมาะสม) เมื่อใช้วัตถุเป็นลวดลายลวดลายมันจะสะดวกในการกำหนดให้กับหนึ่งในกลุ่มจุดคริสตัล: ใน 2-D มี 10 สิ่งเหล่านี้ (แสดงด้านล่าง);ใน 3-D มี 32-

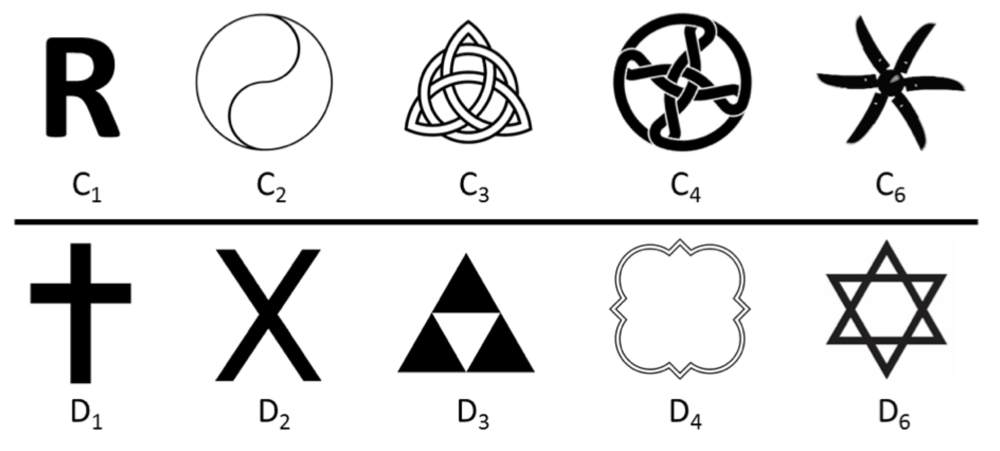
ในสัญกรณ์ที่เรียกว่าสัญลักษณ์ของ Schoenfliesหลังจาก Arthur Moritz Schoenflies นักคณิตศาสตร์ชาวเยอรมัน:

• “ C” ย่อมาจาก“ Cyclic” วัตถุเหล่านี้มีความสมมาตรแบบหมุนได้ แต่ไม่มีสมมาตรสะท้อนแสง ตัวเลขระบุว่ามีความสมมาตรแบบหมุนได้เท่าไหร่ดังนั้นสัญลักษณ์ที่มีป้ายกำกับ C2 มีความสมมาตรสองเท่า รูปแบบวงจรทั้งหมดมีภาพสะท้อนของกระจกที่“ หมุนไปทางอื่น”
• “ D” หมายถึง“ dihedral” วัตถุเหล่านี้มีทั้งความสมมาตรแบบสะท้อนแสงและการหมุน จำนวนบ่งบอกถึงความสมมาตรแบบหมุนได้ที่พวกเขามีเช่นเดียวกับจำนวนเส้นสมมาตร

ตาข่าย

ตาข่ายเป็นรูปแบบการทำซ้ำของจุดในอวกาศที่สามารถทำซ้ำวัตถุ (หรือแม่นยำมากกว่าแปล, ร่อนสะท้อนหรือหมุนสกรู) ใน 1-D มีเพียงหนึ่งตาข่ายใน2-D มีห้าและใน 3-D มี 14-

ในการสร้างรูปแบบวัตถุ 2-D (ซึ่งจะมีหนึ่งใน 10 กลุ่มจุดผลึกที่ได้รับมอบหมาย) จะถูกทำซ้ำตามโครงตาข่าย 1-D หรือ 2-D วัตถุ 2-D ซ้ำไปตามรูปแบบ 1-D รูปแบบหนึ่งของกลุ่ม Frieze เจ็ดกลุ่ม- วัตถุ 2 มิ17 กลุ่มวอลล์เปเปอร์-

รูปแบบ 3 มิติมีความซับซ้อนมากขึ้นและไม่ค่อยพบนอกผลึก กลุ่มจุด 3 มิติต่าง ๆ ซ้ำไปตามรูปแบบ 3 มิติต่างๆกลุ่มอวกาศ 230 สายพันธุ์- วัตถุ 3-D สามารถทำซ้ำได้ตามเส้นขัด 1-D หรือ 2-D เพื่อผลิตกลุ่มก้านหรือกลุ่มเลเยอร์ตามลำดับ

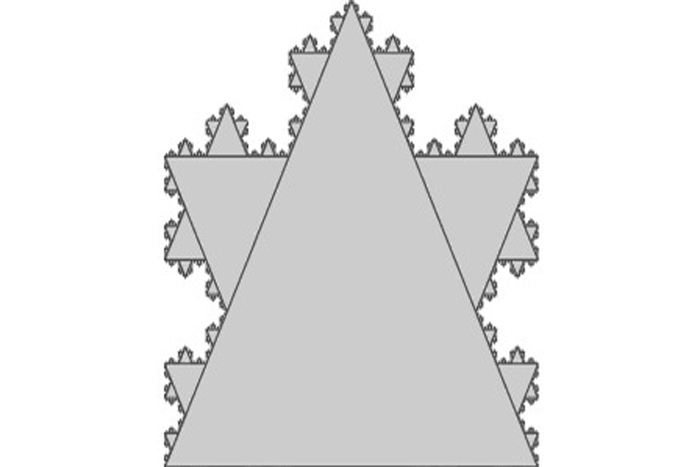
เศษส่วน

สิ่งสำคัญคือความแปรปรวนภายใต้การเปลี่ยนแปลงประเภทที่สี่: การปรับขนาด วงกลมศูนย์กลางของเส้นผ่านศูนย์กลางที่คืบหน้าทางเรขาคณิตเป็นค่าคงที่ภายใต้การปรับขนาด เมื่อวัตถุนั้นไม่เปลี่ยนแปลงภายใต้การผสมผสานการแปลการสะท้อนการหมุนและการปรับขนาดเฉพาะมันจะสร้างรูปแบบใหม่ที่เรียกว่ากเศษส่วน-

ทรัพยากรเพิ่มเติม

• สมมาตร: วารสารการเข้าถึงแบบเปิดครอบคลุมการวิจัยเกี่ยวกับปรากฏการณ์สมมาตรไม่ว่าพวกเขาจะเกิดขึ้นที่ไหนในการศึกษาทางคณิตศาสตร์และวิทยาศาสตร์
• มหาวิทยาลัย Otterbein:ทรัพยากรสมมาตร- เพื่อช่วยเหลือนักเรียนเรียนรู้แนวคิดเกี่ยวกับความสมมาตรของโมเลกุลและเพื่อช่วยคณาจารย์สอนแนวคิดของความสมมาตรของโมเลกุล
• Nanyang Technological University ในสิงคโปร์เปิดสอนหลักสูตรออนไลน์ "ความงามรูปแบบและฟังก์ชั่น: การสำรวจสมมาตร-