Honeycombs พื้นห้องน้ำและการออกแบบโดยศิลปิน MC Escher มีบางอย่างที่เหมือนกัน: พวกเขาประกอบด้วยรูปแบบการทำซ้ำรูปทรงเดียวกันโดยไม่มีการทับซ้อนหรือช่องว่างใด ๆ รูปแบบประเภทนี้เรียกว่าการปูกระเบื้องหรือ tessellation
คำว่า "tessellate" หมายถึงการสร้างหรือจัดเรียงสี่เหลี่ยมเล็ก ๆ ในรูปแบบตาหมากรุกหรือโมเสคตามมหาวิทยาลัย Drexel- มันมาจากภาษากรีกคนขี้เกียจซึ่งหมายถึง "สี่" การเอียงครั้งแรกทำจากกระเบื้องสี่เหลี่ยม ในฐานะที่เป็นรูปแบบศิลปะ Tessellation นั้นอุดมไปด้วยคณิตศาสตร์โดยเฉพาะอย่างยิ่งกับความสัมพันธ์กับเรขาคณิตทอพอโลยีและทฤษฎีกลุ่ม วัฒนธรรมตั้งแต่ไอริชและอาหรับไปจนถึงอินเดียและจีนล้วนได้ฝึกฝนการปูกระเบื้องในระดับความซับซ้อนต่าง ๆ มาสำรวจความหลากหลายของ tessellations ที่เราพบในธรรมชาติการออกแบบการทำงานและศิลปะ
tessellations ปกติ
ในแง่คณิตศาสตร์ "ปกติ" อธิบายรูปร่างใด ๆ ที่มีด้านที่เท่ากันและมุมที่เท่ากัน มีสามรูปร่างปกติที่ประกอบขึ้นเป็น tessellations ปกติ: สามเหลี่ยมด้านเท่า, สี่เหลี่ยมจัตุรัสและหกเหลี่ยมปกติ ตัวอย่างเช่นมีการใช้หกเหลี่ยมปกติในรูปแบบของรังผึ้งโครงสร้างการทำรังของผึ้ง
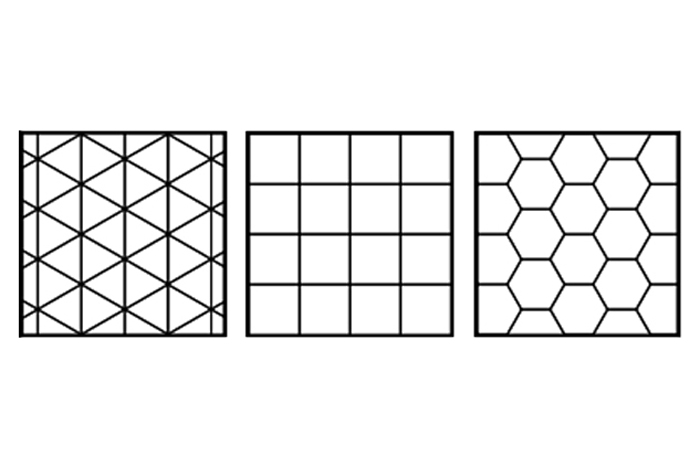
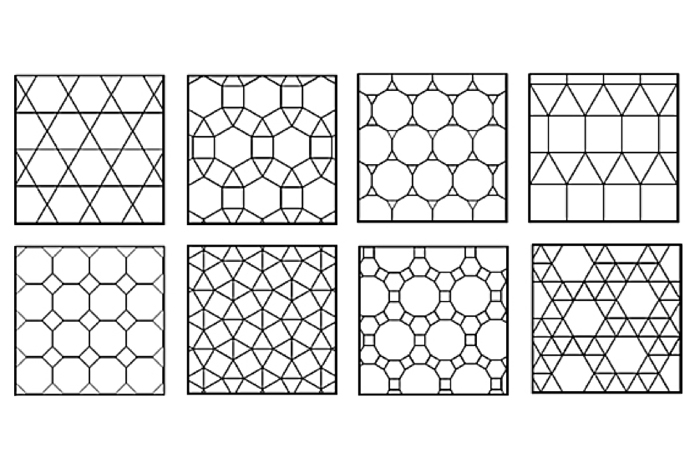
tessellations กึ่งธรรมดา
tessellations กึ่งปกติทำจากรูปหลายเหลี่ยมมากกว่าหนึ่งชนิด ภายในขีด จำกัด ของรูปร่างเดียวกันโดยรอบจุดสุดยอดแต่ละจุด (จุดที่มุมพบ) มีแปด tessellations ดังกล่าว tessellation กึ่งปกติแต่ละรายการมีชื่อสำหรับจำนวนด้านของรูปร่างที่อยู่รอบ ๆ แต่ละจุดยอด ตัวอย่างเช่นสำหรับการปูกระเบื้องแรกด้านล่างแต่ละจุดสุดยอดประกอบด้วยจุดของรูปสามเหลี่ยม (3 ด้าน), หกเหลี่ยม (6), สามเหลี่ยมอีกรูปสามเหลี่ยม (3) และอีกหกเหลี่ยม (6) ดังนั้นจึงเรียกว่า 3.6.3.6 บางครั้ง tessellations เหล่านี้ได้รับการอธิบายว่าเป็น "อาร์คิมดีน" เพื่อเป็นเกียรติแก่นักคณิตศาสตร์กรีกศตวรรษที่สาม
monohedral tessellations
"โมโน" หมายถึง "หนึ่ง" และ "-hedral" หมายถึง "รูปร่าง"; ดังนั้น tessellations monohedral นั้นประกอบไปด้วยรูปร่างเดียวแม้ว่ารูปร่างอาจหมุนหรือพลิกได้ ในภาษาของคณิตศาสตร์รูปร่างในรูปแบบดังกล่าวได้รับการอธิบายว่าสอดคล้องกัน รูปสามเหลี่ยมทุกรูป (รูปสามด้าน) และทุกรูปสี่เหลี่ยม (รูปทรงสี่ด้าน) มีความสามารถในการ tessellation อย่างน้อยหนึ่งวิธีแม้ว่าจะมีเพียงไม่กี่คนที่สามารถเลือก tessellate ได้มากกว่าหนึ่งวิธี ตัวอย่างบางส่วนแสดงด้านล่าง:
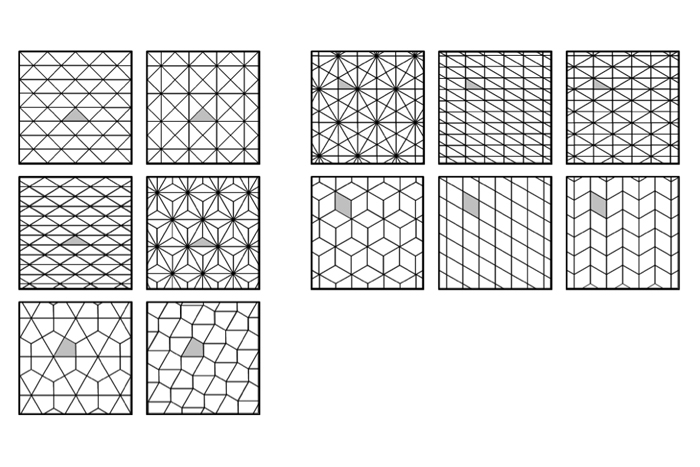
นักคณิตศาสตร์ Eric W. Weisstein จาก Wolfram Research'sคณิตศาสตร์สำหรับ Pentagons ปัจจุบันมีรูปร่างที่รู้จัก 14 ชั้นที่จะ Tessellate และมีเพียงสามคนเท่านั้น ไม่ว่าจะมีชั้นเรียนมากขึ้นหรือไม่ยังคงเป็นปัญหาทางคณิตศาสตร์ที่ยังไม่ได้รับการแก้ไข สำหรับรูปร่างที่มีเจ็ดข้างขึ้นไปไม่มีรูปหลายเหลี่ยม tessellate เช่นนั้นเว้นแต่พวกเขาจะมีมุมมากกว่า 180 องศา รูปหลายเหลี่ยมดังกล่าวถูกอธิบายว่าเป็นเว้าเพราะมีการเยื้อง
ตัวอย่างของ tessellations รูปสี่เหลี่ยมขนมเปียกปูนแสดงอยู่ด้านล่าง Tessellation Pentagonal 14 คลาสทั้งหมดสามารถสร้างได้ที่โครงการสาธิต Wolfram-
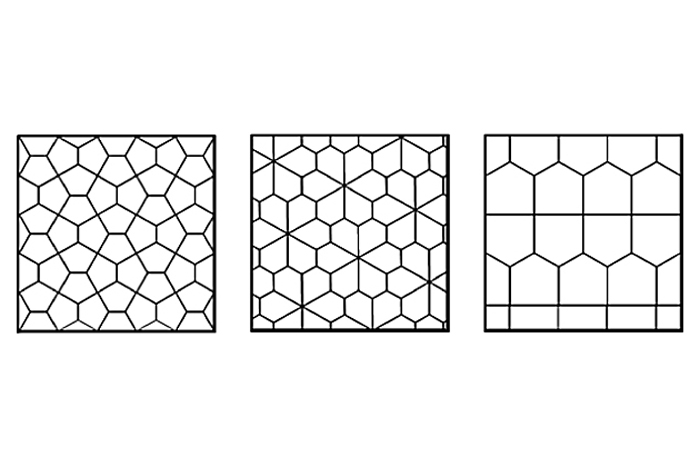
คู่
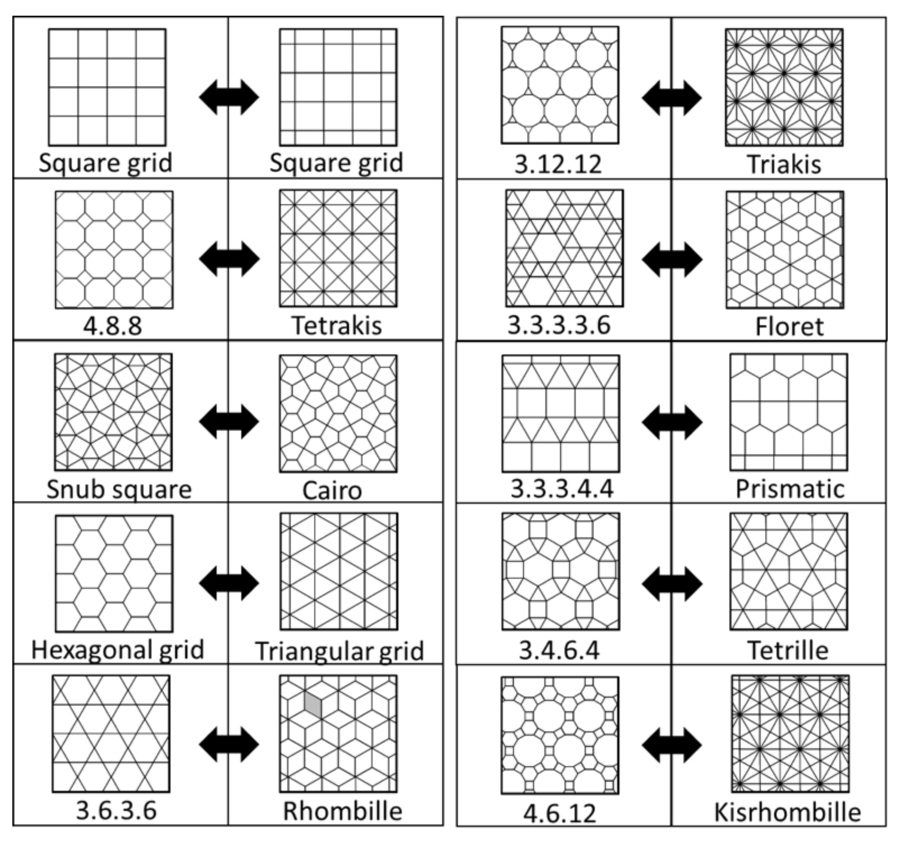
มีการเชื่อมต่อที่ลึกซึ้งยิ่งขึ้นที่วิ่งผ่าน tessellations ทางเรขาคณิตเหล่านี้จำนวนมาก พวกเขาส่วนใหญ่เป็น "คู่" ของกันและกัน ตามที่ Branko Grünbaumผู้เขียน "การเอียงและรูปแบบ"(Freeman, 1987) เพื่อสร้างคู่ของ Tessellation วาดจุดตรงกลางของแต่ละรูปร่างเชื่อมต่อแต่ละจุดเข้ากับจุดของรูปร่างที่อยู่ใกล้เคียงแต่ละจุดและลบรูปแบบดั้งเดิมด้านล่างเป็นตัวอย่างของ tessellations และคู่ของพวกเขา:
MC ESCHER & MODIFIED MONOHEDRAL TESSELLATIONS
รูปแบบศิลปะที่ไม่เหมือนใครถูกเปิดใช้งานโดยการปรับเปลี่ยน monohedral tessellations ผู้ประกอบการที่มีชื่อเสียงที่สุดของเรื่องนี้คือ 20ไทย-MC Escher ศิลปินที่มีความสำคัญ อ้างอิงจาก James Case ผู้ตรวจสอบหนังสือสำหรับสังคมเพื่ออุตสาหกรรมและคณิตศาสตร์ประยุกต์(สยาม) ในปี 1937 Escher แบ่งปันกับภาพร่างพี่ชายของเขาจากความหลงใหลของเขากับ 11ไทย- และ 12ไทย-งานศิลปะอิสลามในศตวรรษของคาบสมุทรไอบีเรีย พี่ชายของเขาสั่งให้เขาไปยังบทความทางวิทยาศาสตร์ในปี 1924 โดย George Pólyaซึ่งแสดงให้เห็นถึง 17 วิธีที่รูปแบบสามารถจัดหมวดหมู่ได้ด้วยความสมมาตรที่หลากหลาย สิ่งนี้เป็นแรงบันดาลใจให้ Escher ซึ่งเริ่มสำรวจ tessellations ที่เชื่อมโยงกันอย่างลึกซึ้งของสัตว์ผู้คนและพืช
ตามที่ Escher "Crystallographer มี ... ยืนยันว่าและมีวิธีการแบ่งเครื่องบินในลักษณะปกติในการทำเช่นนั้นพวกเขาได้เปิดประตูที่นำไปสู่โดเมนที่กว้างขวาง แต่พวกเขาไม่ได้เข้าไปในโดเมนนี้เอง
tessellation "Gecko" ต่อไปนี้ซึ่งได้รับแรงบันดาลใจจากการออกแบบ Escher ที่คล้ายกันนั้นขึ้นอยู่กับกริดหกเหลี่ยม สังเกตว่าตุ๊กแกแต่ละตัวสัมผัสกับคนอื่นอีกหกคน

Aperiodic tessellations
ไม่ใช่ทุก tessellations ซ้ำ รูปแบบดังกล่าว (ถ้ามันสามารถเรียกได้ว่า) อธิบายว่า "Aperiodic" ด้านล่างนี้คือการปูกระเบื้อง Penrose สามรุ่นซึ่งตั้งชื่อตามนักฟิสิกส์คณิตศาสตร์ชาวอังกฤษ Rodger Penrose ซึ่งตีพิมพ์รูปแบบดังกล่าวเป็นครั้งแรกในปี 1974 ที่ University of Oxford รูปแบบเหล่านี้มีความสมมาตรห้าเท่าซึ่งเป็นคุณสมบัติที่ไม่พบในรูปแบบ (ซ้ำ) เป็นระยะ
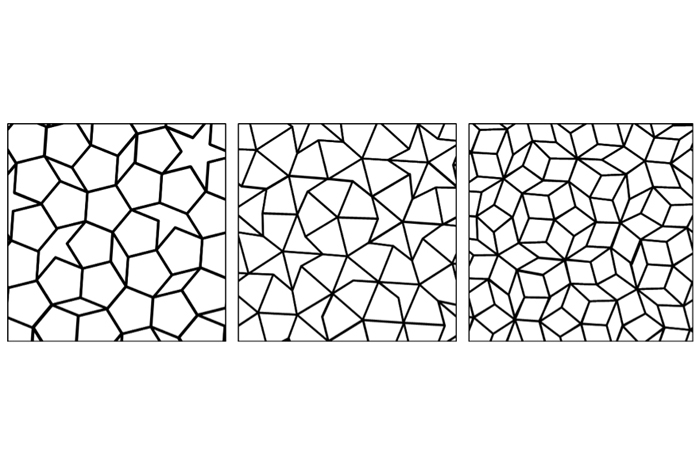
สถาปัตยกรรมอิสลามยุคกลางมีความอุดมสมบูรณ์โดยเฉพาะอย่างยิ่งใน tessellation aperiodic รูปแบบถูกใช้ในงานศิลปะและสถาปัตยกรรมอย่างน้อย 500 ปีก่อนที่พวกเขาจะถูกค้นพบในตะวันตก ตัวอย่างแรก ๆ คือ Gunbad-I Qabud, หอหลุมฝังศพ 1197 แห่งใน Maragha, อิหร่าน ตามarchnetห้องสมุดสถาปัตยกรรมออนไลน์พื้นผิวด้านนอก "ถูกปกคลุมไปด้วยรูปแบบอิฐของเพนทาอนที่เชื่อมโยงกัน"
รูปทรงเรขาคณิตภายใน tessellations aperiodic symmetrical symmetrical ได้กลายเป็นสิ่งสำคัญต่อสนามผลึกซึ่งนับตั้งแต่ทศวรรษ 1980 ได้ก่อให้เกิดการศึกษาของ quasicrystal จากข้อมูลของ Peter J. Lu นักฟิสิกส์ที่ Harvard, quasicrystal โลหะมี "ความต้านทานความร้อนและไฟฟ้าสูงผิดปกติเนื่องจาก aperiodicity" ของการเตรียมอะตอมของพวกเขา
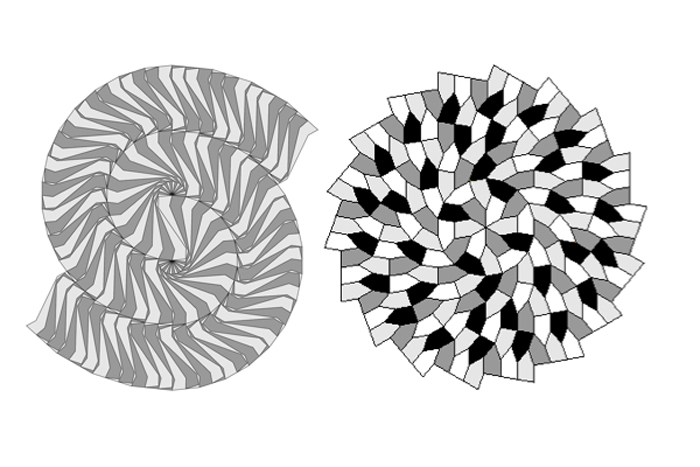
อีกชุดหนึ่งของ tessellations aperiodic ที่น่าสนใจคือเกลียว รูปแบบแรกดังกล่าวถูกค้นพบโดย Heinz Voderberg ในปี 1936 และใช้รูปหลายเหลี่ยม 11 ด้านเว้า (แสดงทางด้านซ้าย) การปูกระเบื้องเกลียวอีกครั้งถูกตีพิมพ์ในปี 1985 โดย Michael D. Hirschhorn และ DC Hunt โดยใช้เพนตากอนที่ผิดปกติ (แสดงทางด้านขวา)
ทรัพยากรเพิ่มเติม
- ดู Tessellations ของ MC Escher ที่MC Escher Gallery-
- ดูวิดีโอ YouTube นี้เพื่อเรียนรู้เพิ่มเติมเกี่ยวกับการเอียงของเพนโรส
- เรียนรู้เพิ่มเติมเกี่ยวกับแนวคิดของ Peter J. Lu เกี่ยวกับเรขาคณิตของสถาปัตยกรรมอิสลามยุคกลาง-