ทอพอโลยีคืออะไร?

ทอพอโลยีเป็นสาขาวิชาคณิตศาสตร์ที่อธิบายพื้นที่คณิตศาสตร์โดยเฉพาะอย่างยิ่งคุณสมบัติที่เกิดจากรูปร่างของพื้นที่ นักโทโพโลยีของรูปร่างหลายคนจัดการกับเรื่องแปลกอย่างไม่น่าเชื่อมากจนในชีวิตประจำวันของทุกวันเช่นชามและสัตว์เลี้ยงและต้นไม้ประกอบขึ้นเป็นชนกลุ่มน้อย คำว่า "ทอพอโลยี" มาจากคำภาษากรีกสำหรับสถานที่ (topos) และการศึกษา (-logy-

ทอพอโลยีมีความสำคัญในการเป็นแนวทางในการศึกษาหลายด้าน:

• ฟิสิกส์เชิงทฤษฎี (โดยเฉพาะอย่างยิ่งผู้สืบทอดของกลศาสตร์ควอนตัมเช่นทฤษฎีฟิลด์ควอนตัมและทฤษฎีสตริง)
• จักรวาลวิทยา (สำหรับการกำหนดรูปร่างของจักรวาล)
• ชีววิทยา (สำหรับการพันกันของ DNA และทำนายการเจริญเติบโตของอวัยวะและส่วนอื่น ๆ ของร่างกาย)
• วิทยาการคอมพิวเตอร์ (สำหรับการกำหนดโครงสร้างขนาดใหญ่ของชุดข้อมูล)
• หุ่นยนต์ (ที่ซึ่งการเคลื่อนไหวของแขนหุ่นยนต์ได้รับการวางแผนตามรูปร่างของพื้นที่ที่มีหลายมิติเท่ากับจำนวนข้อต่อแขน)

การเสียรูปอย่างต่อเนื่อง

คุณสมบัติการศึกษาของโทโพลิ่งของรูปร่างโดยเฉพาะอย่างยิ่งที่ได้รับการเก็บรักษาไว้หลังจากรูปร่างถูกบิดยืดหรือผิดรูป รายการของการเปลี่ยนแปลงที่ได้รับอนุญาตทั้งหมดพอดีภายใต้แนวคิดทางคณิตศาสตร์ที่เรียกว่าการเสียรูปอย่างต่อเนื่องซึ่งหมายถึง“ การยืด แต่ไม่ฉีกขาดหรือรวมกัน” ตัวอย่างเช่นวงกลมอาจถูกดึงและยืดออกเป็นวงรีหรือสิ่งที่ซับซ้อนเช่นโครงร่างของการพิมพ์มือ การฉีกขาดและการรวมกันทำให้เกิดสิ่งที่เรียกว่าความไม่ต่อเนื่องดังนั้นพวกเขาจึงไม่ได้รับอนุญาต

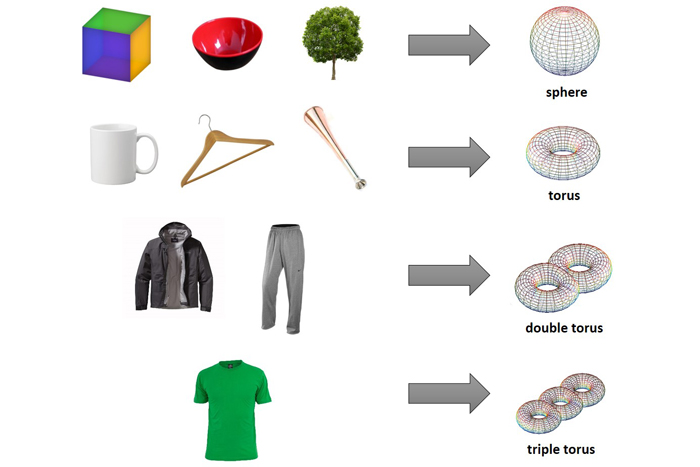
วัตถุสองชิ้นที่สามารถยืดออกเป็นรูปร่างเดียวกันได้อธิบายไว้เป็นเกี่ยวกับ homeomorphicจากภาษากรีกละตินสำหรับ“ คล้ายกับ” (homo-) และกรีก“ รูปแบบรูปร่างหรือรูป” (morphe- ผ่านเลนส์นี้วัตถุในชีวิตประจำวันแทบทุกชนิดเป็น homeomorphic ที่มีทรงกลม (ลูกบอล) หรือ torus ที่หลากหลาย (โดนัท)

ทอพอโลยีบางสาขาอนุญาตให้วัตถุผ่านตัวเองในขณะที่ถูกยืดออก; คนอื่นไม่ได้ เมื่อพิจารณาพื้นผิวนั้นสามารถผ่านตัวเองเป็นสิ่งสำคัญที่จะไม่หยิกพื้นผิวแน่นอย่างไม่สิ้นสุดเนื่องจากสิ่งนี้ยังเพิ่มความไม่ต่อเนื่อง สิ่งนี้มักจะพบเมื่อพื้นผิวกลับมาเป็นสองเท่าของตัวเองเช่นเมื่อพยายามหมุนทรงกลมภายใน (ซึ่งยาก แต่เป็นไปได้)

ออยเมอร์

ตัวอย่างหนึ่งของคุณสมบัติที่ไม่เปลี่ยนแปลงภายใต้การเสียรูปอย่างต่อเนื่องคือวัตถุของวัตถุออยเมอร์ตั้งชื่อตาม Leonhard Euler อายุ 18 ปี^ไทย-นักคณิตศาสตร์ชาวเยอรมันในศตวรรษที่

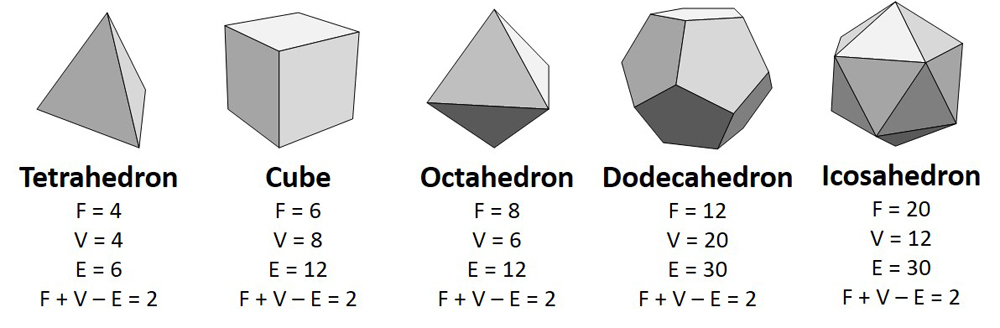
เพื่อแสดงให้เห็นถึงลักษณะออยเลอร์ของวัตถุก่อนอื่นเราใช้ทรงกลม (หรือวัตถุ homeomorphic ที่มีทรงกลมเช่นหัวมนุษย์) และกระเบื้องพื้นผิวด้วยรูปหลายเหลี่ยม จากนั้นเรานับจำนวนใบหน้า (ด้านข้าง), ขอบ (สถานที่ที่ทั้งสองฝ่ายพบกัน) และจุดยอด (สถานที่ที่มีสามด้านหรือมากกว่า) ตอนนี้เพิ่มจำนวนใบหน้า (F) และจุดยอด (V) และลบจำนวนขอบ (E): F + V - E มันไม่สำคัญว่าคุณจะแบ่งพื้นผิวอย่างไร คำตอบจะออกมาเหมือนกันเสมอ: สอง เนื่องจากของแข็งห้าตัว (รูปร่าง 3 มิติที่ทำจากรูปหลายเหลี่ยมแบบปกติหนึ่งชนิด) ล้วนเป็น homomorphic ไปยังทรงกลมพวกเขาทั้งหมดยังมีลักษณะออยเลอร์ของสอง

เราสามารถเข้าใจได้ว่าทำไมลักษณะออยเลอร์ได้รับการอนุรักษ์ถ้าเราคิดเกี่ยวกับความหมายของการเพิ่มขอบหรือจุดสุดยอด การเพิ่มขอบระหว่างจุดยอดสองจุดจะแยกใบหน้าหนึ่งออกเป็นสอง: ขอบเพิ่มหนึ่งใบหน้าเพิ่มขึ้นหนึ่งและจุดยอดยังคงเหมือนเดิม ในทำนองเดียวกันการเพิ่มจุดสุดยอดตามขอบจะแยกขอบออกเป็นสอง: ขอบเพิ่มหนึ่ง, จุดยอดเพิ่มหนึ่งและใบหน้ายังคงเหมือนเดิม

ตอนนี้กระเบื้องพื้นผิวของ torus, count f, v และ e และคุณจะได้รับลักษณะออยเมอร์เป็นศูนย์ นี่คือตัวอย่าง:

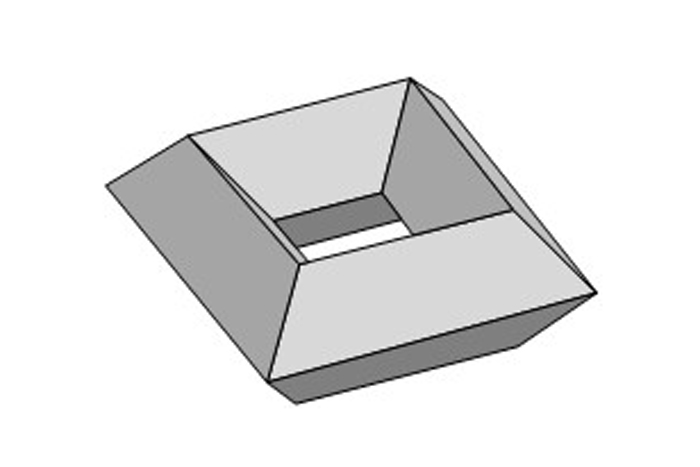
ด้วย torus คู่ลักษณะออยเลอร์เป็นลบสอง; สำหรับตรีสามตัวลบสี่ แต่ละหลุมเพิ่มเติมจะช่วยลดลักษณะออยเลอร์ได้สอง

พื้นผิวที่ไม่สามารถมุ่งเน้นได้

สิ่งหนึ่งที่รูปร่างทั้งหมดที่เราได้พูดคุยเกี่ยวกับตอนนี้มีเหมือนกันคือพวกเขากล่าวกันว่าเป็นปรับได้- ซึ่งหมายความว่าข้อผิดพลาดที่เดินอยู่บนพื้นผิวด้านนอกจะยังคงอยู่ด้านนอกเสมอ เช่นเดียวกันสำหรับด้านใน นอกจากนี้ยังมีไม่สามารถทำได้พื้นผิวหมายถึงข้อผิดพลาดที่หลงทางบนพื้นผิวสามารถจบลงได้ทั้งสองด้าน ตัวอย่างที่มีชื่อเสียงที่สุดของเรื่องนี้คือแถบ Mobius(ซึ่งมีลักษณะออยเมอร์เป็นศูนย์, EC = 0)

ในขณะที่ภาษาเช่น“ ทั้งสองด้านของแถบ Mobius” มีประโยชน์สำหรับการแนะนำแนวคิด แต่มันก็สามารถตอบโต้ได้กับจิตใจของนักโทญ่าที่กล่าวว่าพื้นผิวใด ๆ คือ 2-D และเป็นสิ่งมีชีวิตที่อาศัยอยู่ ผ่านเลนส์นี้มันมีประโยชน์มากกว่าที่จะคิดว่ามีแมลง 2 มิติอยู่ภายในพื้นผิวของตัวเอง สำหรับพื้นผิวที่สามารถปรับได้มีข้อบกพร่องมือขวาและข้อบกพร่องด้านซ้ายมือ แต่สำหรับพื้นผิวที่ไม่สามารถมุ่งเน้นได้ข้อบกพร่องด้านขวาและมือซ้ายจะแยกไม่ออก สิ่งนี้เน้นว่าแถบ Mobius แสดงถึงพื้นที่และเราสนใจในคุณสมบัติที่เกิดจากรูปร่างของพื้นที่

รูปหลายเหลี่ยมพื้นฐาน

ด้วยมุมมองของพื้นผิวที่เป็น 2-D จึงสะดวกในการเป็นตัวแทนของพื้นที่ทอพอโลยีในแง่ของพวกเขารูปหลายเหลี่ยมพื้นฐาน- ในการเปลี่ยนพื้นผิว 2 มิติของรูปหลายเหลี่ยมพื้นฐานให้กลายเป็นวัตถุ 3 มิติยืดพื้นผิวเพื่อให้ด้านที่สอดคล้องกันเข้าร่วมในทิศทางที่ระบุโดยลูกศร ดังที่เห็นได้การเข้าร่วมด้านคู่ขนานทำให้กระบอกสูบ (EC = 0) และการเข้าร่วมเส้นต่อต้านขนานทำให้แถบ mobius (EC = 0)

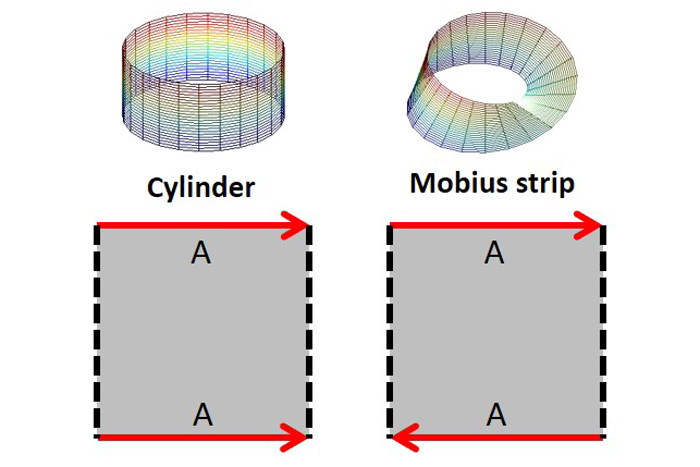
ข้อผิดพลาด 2 มิติที่เดินออกไปและลูกศรของรูปหลายเหลี่ยมพื้นฐานจะถูกส่งไปยังขอบเขตอื่น ๆ และมุ่งเน้นไปที่วิธีเดียวกันเมื่อเทียบกับทิศทางของลูกศร ไม่ว่าข้อผิดพลาดจะยังคงเหมือนเดิมหรือพลิกระบุว่าพื้นผิวนั้นสามารถปรับทิศทางได้หรือไม่สามารถมุ่งเน้นได้ตามลำดับ ข้อผิดพลาด 2 มิติไม่ได้รับอนุญาตให้ข้ามขอบเขตประ

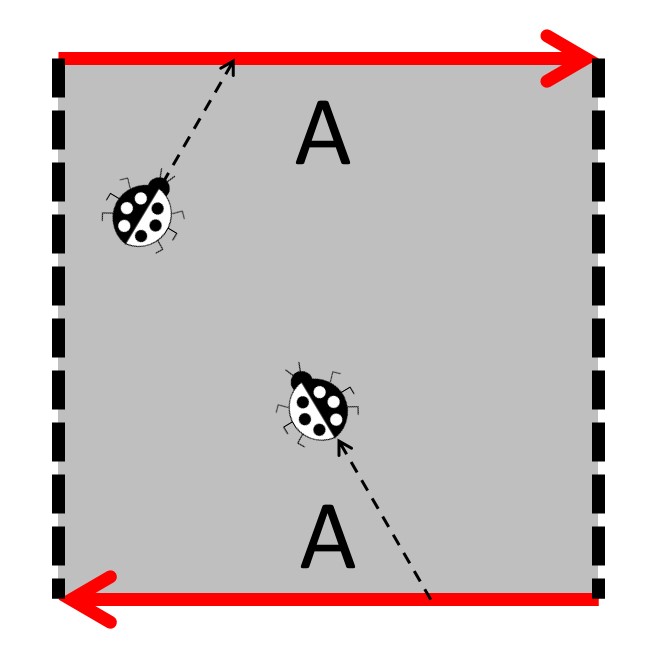
รูปร่างแรกที่เราพูดถึงยังมีรูปหลายเหลี่ยมพื้นฐาน ในการทำ torus ก่อนอื่นทำกระบอกสูบจากนั้นยืดปลายกระบอกสูบจนกว่าพวกเขาจะพบกัน ในการสร้างทรงกลมให้พับแผ่นจากมุมหนึ่งไปยังอีกมุมหนึ่งเพื่อทำซองรูปสามเหลี่ยมแล้วพองมันจนกระทั่งเป็นทรงกลม

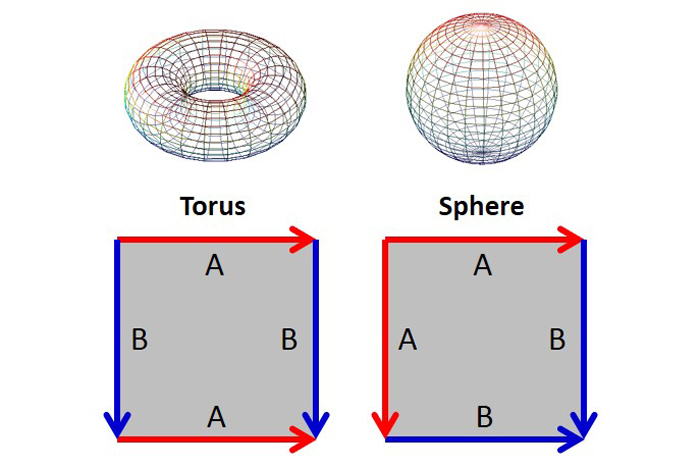
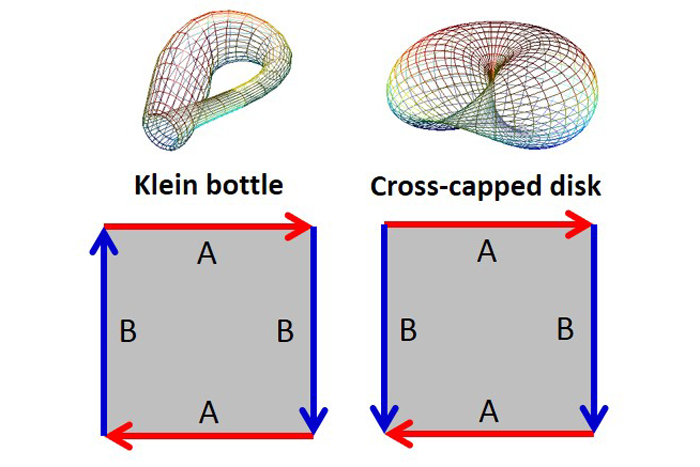
ขอบประของแถบ Mobius สามารถรวมกันได้สองวิธีที่แตกต่างกันเพื่อก่อให้เกิดพื้นผิวที่ไม่สามารถมุ่งเน้นได้สอง: ขวด Klein (EC = 0) สามารถคิดได้ว่าเป็นข้ามระหว่างแถบ Mobius และกระบอกสูบและดิสก์ข้ามปกคลุม (EC = 1) เช่นเดียวกับแถบ Mobius หากมีมิติที่สามในการห่อแผนที่นี้เราสามารถได้รับมุมมองบางอย่างของ "รูปร่าง" โดยรวมของพื้นที่ สิ่งปลูกสร้างทั้งสองต้องการให้พื้นผิวได้รับอนุญาตให้ผ่านตัวเอง ข้อผิดพลาด 2 มิติจะไม่สังเกตเห็นทางแยกดังกล่าว เฉพาะที่โลกคือ "พลิก" หลังจากใช้เส้นทางบางอย่างในพื้นที่ 2 มิติ

ปัญหาที่มีชื่อเสียงในทอพอโลยี

โทโพโลยีมีอยู่เพียงไม่กี่ศตวรรษ แต่มีประวัติอันยาวนานของปัญหาและฟิลด์ย่อยที่แต่ละคนมีเรื่องราวของตัวเอง

• สะพานเจ็ดแห่งของKönigsberg: มักจะถือว่าเป็นปัญหาแรกในทอพอโลยี เมืองปรัสเซียนเก่าของKönigsbergเคยมีสะพานเจ็ดแห่งและผู้คนของมันสงสัยว่ามันเป็นไปได้หรือไม่ที่จะเดินเส้นทางที่ข้ามแต่ละสะพานเพียงครั้งเดียว ในปี 1735 ออยเลอร์ได้รับการพิสูจน์แล้วเส้นทางดังกล่าวเป็นไปไม่ได้
• รูปแบบในการพิมพ์ปาล์มและนิ้ว: ลายนิ้วมือทั้งหมดมีคุณสมบัติทั่วไปเช่นลูปและ triradii (สามบรรทัดมารวมกัน) ในปีพ. ศ. 2508 ไลโอเนลเพนโรสนักพันธุศาสตร์ชาวอังกฤษชี้ให้เห็นว่าลายนิ้วมือและงานพิมพ์ปาล์มเชื่อฟังกฎสากล: ทุกคนที่เกิดมาพร้อมกับห้านิ้วมักจะมี triradii มากกว่าลูปสี่เสมอ
• ทฤษฎีบทบอลมีขนดก: สำหรับลูกบอล (หรือทรงกลมค่อนข้าง) ที่ปกคลุมไปด้วยผมมันเป็นไปไม่ได้ที่จะหวีผมทั้งหมด ต้องมีอย่างน้อยหนึ่งที่ที่ผมติดตรง
• Sphere Eversion: สำหรับพื้นผิวทรงกลมที่ได้รับอนุญาตให้ผ่านตัวเองเป็นไปได้หรือไม่ที่จะเปลี่ยนทรงกลมภายในออกอย่างสมบูรณ์โดยไม่ต้องบีบภูมิภาคใด ๆ อย่างไม่ จำกัด ? มันยุ่งยาก แต่ใช่
• ทฤษฎีปม: ทฤษฎี Knot เป็นวินัยภายในทอพอโลยีที่เกี่ยวข้องกับ Tori (พหูพจน์ของ Torus) ที่ไม่สามารถผ่านตัวเองหรือผู้อื่นได้ จุดสนใจที่สำคัญของทฤษฎีปมคือการพิจารณาว่านอตที่ดูแตกต่างกันสองนอตเป็น homeomorphic หรือไม่
• การคาดเดาPoincaré: ในบทความนี้เราได้ตรวจสอบพื้นที่ 2 มิติเท่านั้น แต่ยังมีช่องว่าง 3 มิติที่เชื่อมต่อด้วยวิธีที่แปลก ที่การคาดเดาPoincaréครั้งแรกที่โพสต์ในปี 1904 เป็นเรื่องเกี่ยวกับช่องว่าง 3 มิติเหล่านี้โดยระบุว่า“ ทุกที่เชื่อมต่อกันได้ทุก 3 มิโนโฟลนั้นเป็น homeomorphic กับ 3-sphere” เกือบหนึ่งศตวรรษต่อมาในปี 2000สถาบันคณิตศาสตร์ดินเลือกปัญหา“ Millennium Prize” ที่ยังไม่ได้รับการคัดเลือกซึ่งจะได้รับรางวัล 1 ล้านเหรียญสหรัฐให้กับทุกคนที่หาทางออก การคาดเดาของPoincaréเป็นปัญหาแรกที่แก้ไขได้ นักคณิตศาสตร์ชาวรัสเซีย Grigori Perelman ผู้ซึ่งพบวิธีแก้ปัญหาในปี 2545 ได้ปฏิเสธทั้งรางวัลเงินสดสหัสวรรษและเหรียญภาคสนาม

ทรัพยากรเพิ่มเติม

• zogg จาก betelgeuse: ไม่มีขอบ: รูปร่างของจักรวาล
• สถาบันรอยัล: คณิตศาสตร์สี่มิติ