角質兔子和迷幻分形有什麼共同點？ 物流地圖

分形在數學中佔有一個奇怪的位置。 它們是抽象的進入量子領域的窗口，坐在二維和三維之間的某個地方，並聲稱證明英國海岸線是無限長儘管任何地圖都會告訴你事實並非如此……但它們也非常實用。 以Mandelbrot集為例：

您可能以前看過這種模式，但您有沒有想過它到底意味著什麼？ 儘管曼德布羅特集具有迷幻的表現力，但它與我們周圍的世界有著深厚的聯繫——這一切都取決於一系列數學方程，統稱為物流地圖。

什麼是物流地圖？

邏輯圖在數學界很有名。 它起源於 19 世紀上半葉，是一種對人口動態進行建模的方法，但它已發展成為隨機混沌如何從看似簡單的起點產生的最佳範例之一。 從數學上來說，它看起來像這樣：

用英語來說，這意味著「將當前數字乘以某個常數，可以得到序列中的下一個數字r一個減去它自己”，所以……實際上，你知道嗎——也許舉個例子會更容易。

讓我們選擇作為我們的起點X₀= 1/2 （我們總是選擇 0 到 1 之間的一個值作為起點，1/2 很好並且處於中心位置），我們將設定r成為[旋轉輪盤賭輪] 3. 然後地圖會給我們

另一方面，如果我們設定r= 2.5 我們得到

如果我們增加r最多 3.5 我們有

請記住，邏輯地圖最初是作為人口動態建模的一種方式，這是思考這裡正在發生的事情的一種很好的方式。 假設我們正在模擬一群兔子如何隨時間變化：然後邏輯圖告訴我們，明天我們有多少隻兔子取決於我們今天有多少隻兔子以及繁殖率人口的數量——他們，咳咳，生出新兔子的速度有多快。 我們擁有的兔子越多，可以繁殖的兔子就越多，因此我們將繁殖率乘以目前族群中兔子的數量，X_n。 但如果兔子太多，食物就會耗盡，有些兔子會被迫離開（或挨餓）。 這就是 (1 -X_n）來自——它反映了這樣一個事實：在一座山上只能生活這麼多兔子，然後它們變成為了自己的利益而過於成功。

邏輯地圖儘管表面上很簡單，但卻為我們提供了一個出奇的好預測現實世界中觀察到的人口動態。 換句話說，上面的圖表是使用純數學獲得的，但在正確的情況下（特別是與兔子口渴相關的情況），它們看起來與兔子數量的現實世界數據非常相似。

好吧，很好，但這和曼德布羅特集有什麼關係呢？

好吧，忘記了X值並將邏輯圖視為以下函數r。 沒多久你就會開始看到一些奇怪的行為發生。

讓我們從r= 0。

當圖片改變時r達到一。 在 1 到 3 之間，邏輯圖將帶您到達特定值，無論您選擇什麼作為起點。 有時它會很快，有時會很慢，有時會在到達之前稍微晃動一下，但它總是會在同一點結束（對於觀眾中的書呆子來說，這等於 1-1 /r）。

但在r= 3，有趣的事情發生了：邏輯圖開始振盪。 基本上，您獲得的值開始在兩個固定點之間跳躍。

這會持續到您到達r？ 3.44949（精確形式，r= 1 + ?6)，當您開始看到四個固定點。

然後在r？ 3.54409，它再次發生，然後一次又一次，鏈中的值的數量每次都會加倍。 這一直持續到你達到神奇的數字：r？ 3.56995，此時一切都......崩潰了。

現在是非常酷的部分：如果我們繪製一個圖表r反對X_n, 讓X_n增加，我們得到：

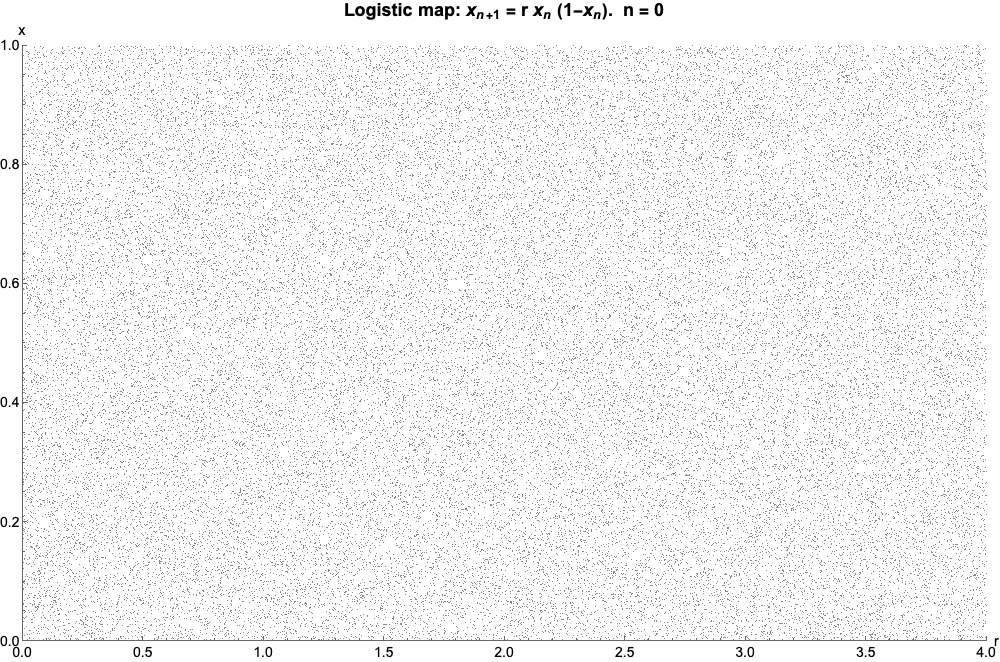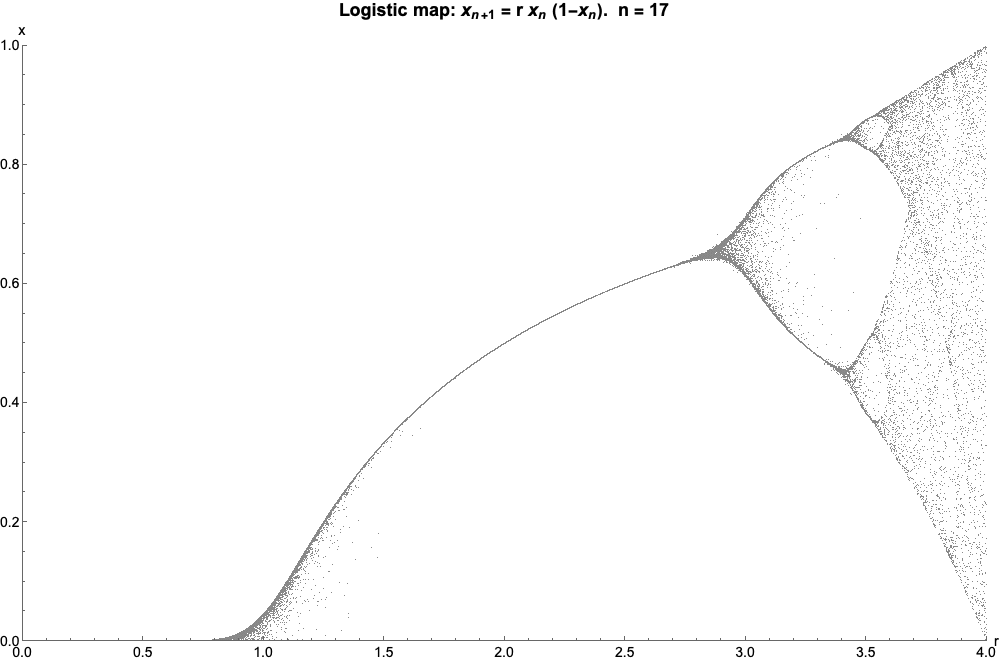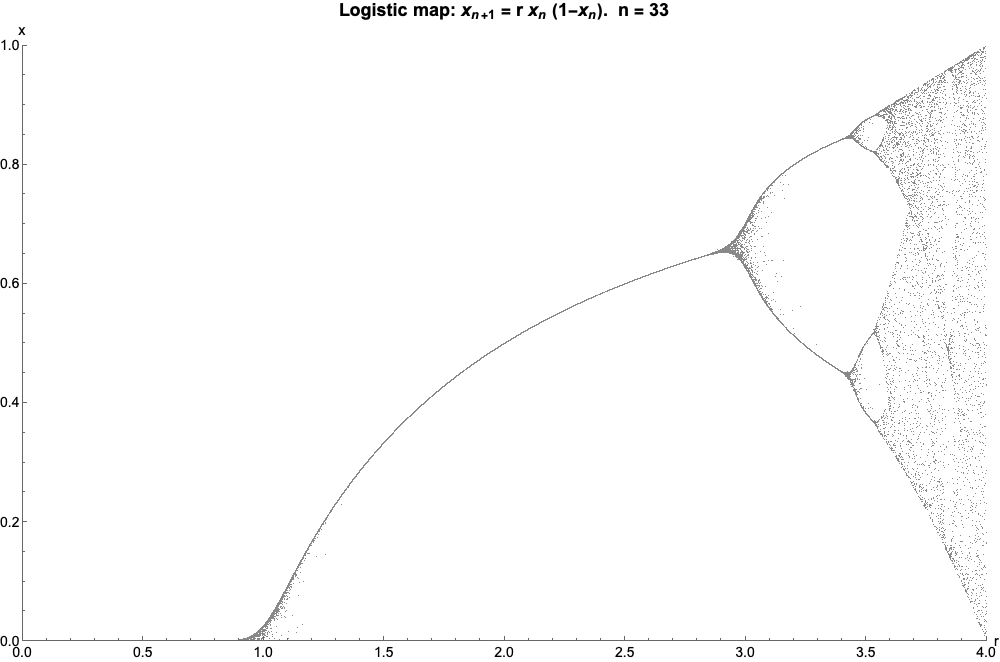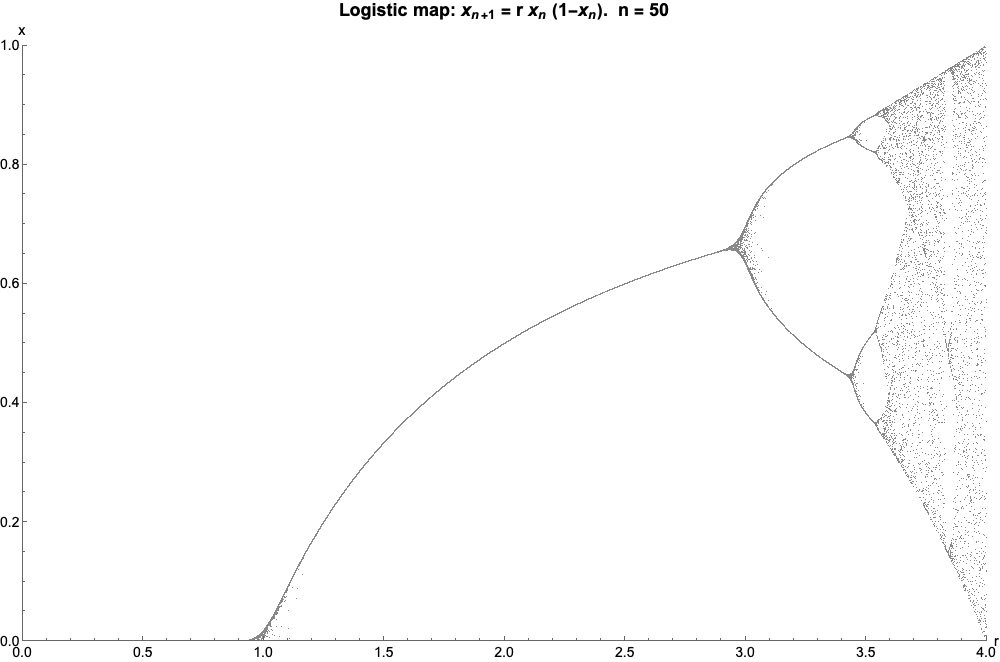
其中，如果我們讓n射向無窮遠，看起來像這樣（稱為邏輯圖的分叉圖）：

和那朋友們， 是曼德布羅特集。

不，說真的。 你看，曼德布羅特集也受遞歸關係的控制——也就是說，透過對你所在的數字做一些事情來給出序列中的下一個數字。 對於邏輯映射，請記住，遞歸關係是

但對於曼德布羅特集來說，

現在，事情變得有點技術性了。 這聽起來似乎很明顯，但無論如何我們都會這麼說：邏輯圖是一個圖，但曼德布羅特集合是一個集合。 令人興奮，我們知道。 但這種差異至關重要，因為這意味著它們告訴我們兩個截然不同——幾乎完全相反的訊息。 雖然邏輯映射要求您提供一些起始值並返回振盪（如果您幸運的話），但曼德爾布羅特集卻說“我們只想要來自此遞歸關係的振盪 - 哪些起始值將為我們提供振盪？”

讓我們再看一個例子，幫助我們理解：讓我們z₀= 0 和C= 1.然後我們發現

序列變得越來越大，沒有界限，所以C= 1 不是 Mandelbrot 集的一部分。 另一方面，如果我們離開z₀= 0 並設定C= -1，我們得到

這些值在 0 和 -1 之間振盪 – 所以C= -1 是 Mandelbrot 集的一部分。 得到它？

好吧，我們不會詳細討論，但相信我們的話：如果你在圖表上畫出所有的複數C從遞歸關係給出有界序列，你會得到：

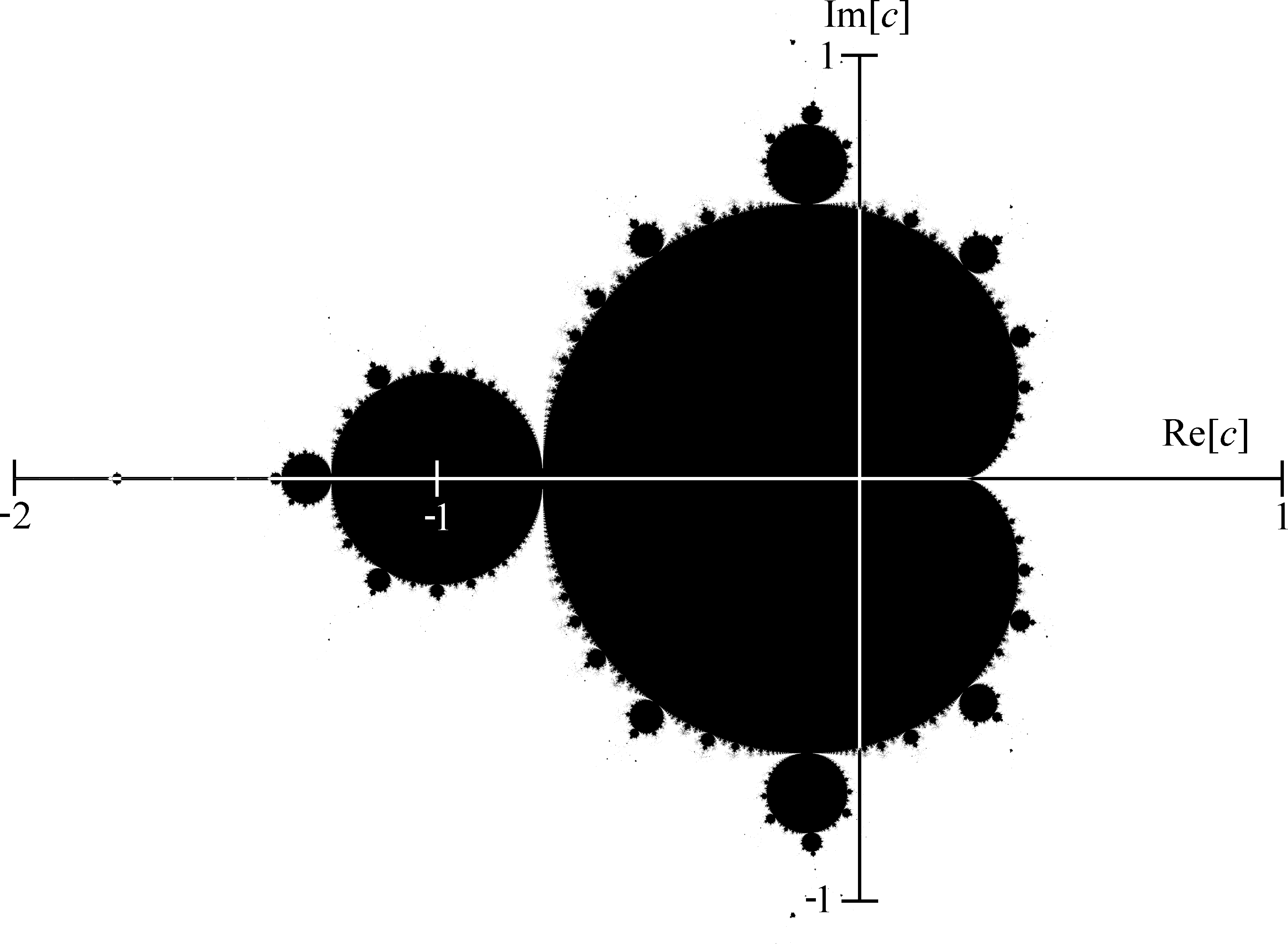
但如果我們想要更多資訊怎麼辦？ 如果我們不僅想知道哪些數值會振盪，還想知道怎麼辦？如何他們振盪嗎？

嗯，這就是奇蹟發生的地方。 看，您可能之前已經注意到，我們將 Mandelbrot 集描述為一組複雜的數字。 如果您不知道它們是什麼，請不要擔心 - 它們基本上只是擴展數軸以包含可以與負數平方的值的一種方法。 但它們的主要特徵是它們是二維的——不是數軸上的點，而是圖表中的某個位置。

但這意味著應用於複數的函數或遞推關係不能給出像我們之前看到的分叉圖那樣漂亮的二維圖——水平「軸」實際上是一個平面。 相反，我們必須將圖表翻轉過來，當我們這樣做時，我們會看到一些東西字面上地驚人的。

物流地圖！ 這不僅僅是一些圖形拼圖——你可以使用冷酷的數學從一個到另一個如果你真的想。 值得注意的是，邏輯圖的分割點對應於曼德布羅特集合與實線相交的邊界——您甚至可以看到曼德布羅特集的「針」所代表的邏輯混亂區域。

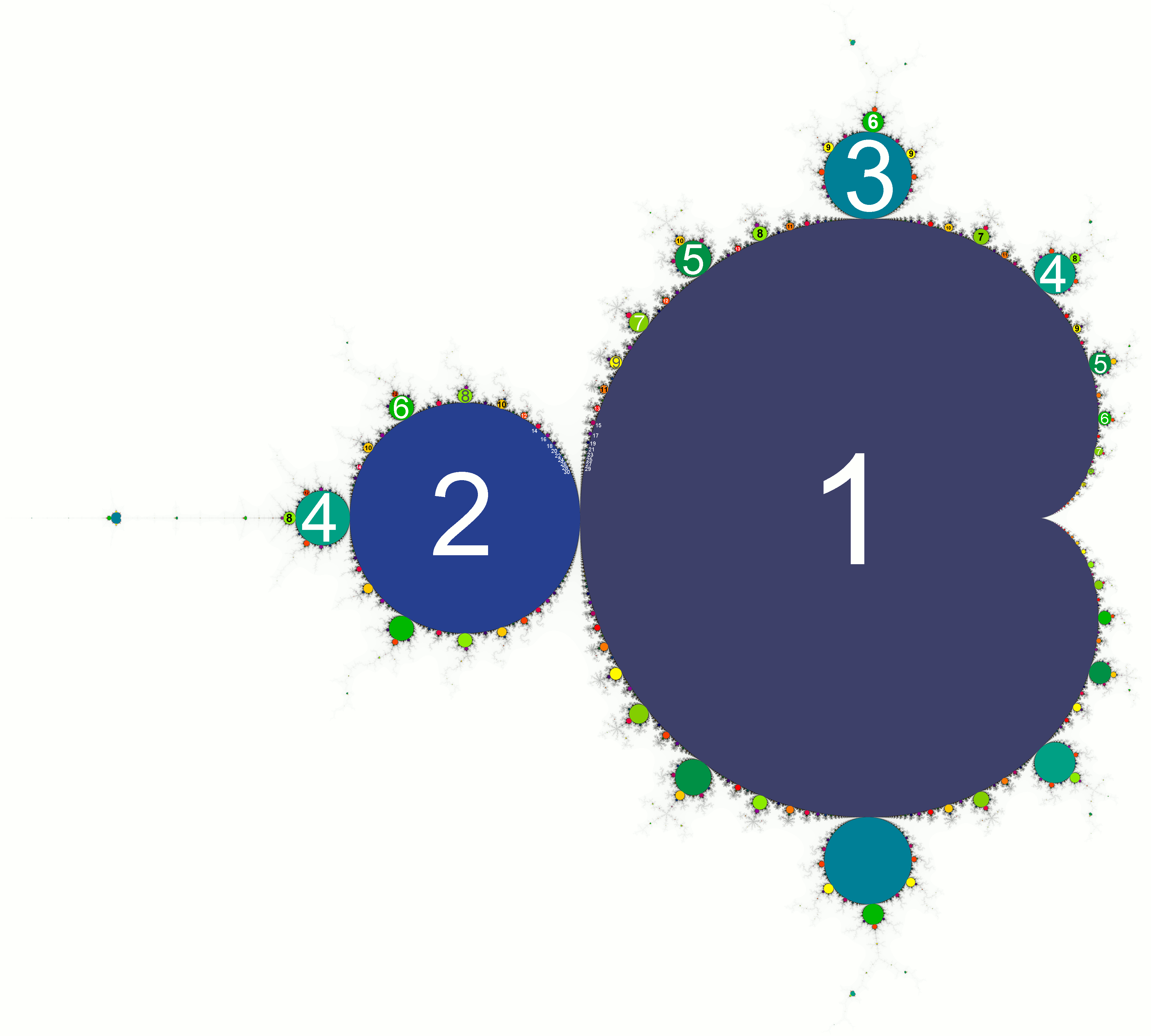
但曼德布羅特集不是僅有的邏輯圖——這只是沿著實軸的部分。 因此，雖然主心形線（曼德布羅分形的最大心形部分）對應於邏輯圖的獨特部分，而主燈泡（分形的第二大部分）對應於圖上振蕩的部分兩個值之間，依序類推到4、8、16 等，Mandelbrot 集合中還有一些部分根本沒有用邏輯圖表示。 像位於主心形線頂部的最大燈泡這樣的部件 - 本部分中的值振盪三倍。 稍微左邊的是一個燈泡，其中包含振盪五次的值。 事實上，您可以選擇任何您喜歡的正整數，並且在 Mandelbrot 集合中的某個位置您可以找到恰好振盪多次的值。

Mandelbrot 集合具有一系列令人驚嘆的品質，其中許多可以在這段史詩般的 Veritasium 視頻，但它與邏輯圖的連結可以說是最令人著迷的之一——即使只是因為它概括了數學的許多精彩之處。

讓我們面對現實：在其他哪個科學領域，你能帶著一群角質兔子想出像曼德布羅特集一樣抽象而美麗的東西？