ในขณะที่อยู่บนเตียงแห่งความตายของเขานักคณิตศาสตร์ชาวอินเดียที่ยอดเยี่ยม Srinivasa Ramanujan เขียนฟังก์ชั่นที่เขาบอกว่ามาหาเขาในความฝันด้วยลางสังหรณ์เกี่ยวกับวิธีที่พวกเขาประพฤติตัว ตอนนี้ 100 ปีต่อมานักวิจัยกล่าวว่าพวกเขาพิสูจน์แล้วว่าเขาพูดถูก
“ เราได้แก้ไขปัญหาจากจดหมายลึกลับคนสุดท้ายของเขาสำหรับคนที่ทำงานในด้านคณิตศาสตร์นี้ปัญหาได้เปิดขึ้นมา 90 ปีแล้ว” นักคณิตศาสตร์มหาวิทยาลัย Emory Ken Ono กล่าว
Ramanujan นักคณิตศาสตร์ที่สอนตัวเองเกิดในหมู่บ้านชนบทในอินเดียใต้ใช้เวลาคิดเกี่ยวกับคณิตศาสตร์มากจนเขาเลิกวิทยาลัยในอินเดียสองครั้ง Ono กล่าว
แต่เขาส่งจดหมายนักคณิตศาสตร์ที่อธิบายงานของเขาและเป็นหนึ่งในนักคณิตศาสตร์ชาวอังกฤษ GH Hardy ที่มีชื่อเสียงมากที่สุดได้รับการยอมรับว่าเป็นอัจฉริยะของเด็กชายอินเดียและเชิญเขาไปที่มหาวิทยาลัยเคมบริดจ์ในอังกฤษเพื่อศึกษา ในขณะนั้น Ramanujan ตีพิมพ์เอกสารมากกว่า 30 ฉบับและได้รับการแต่งตั้งให้เข้าสู่ราชสมาคม -Creative Genius: จิตใจที่ยิ่งใหญ่ที่สุดในโลก-
"สำหรับช่วงเวลาสั้น ๆ ห้าปีเขาสว่างไสวโลกแห่งคณิตศาสตร์ไฟ "โอโน่บอก Livescience
แต่ในที่สุดสภาพอากาศหนาวเย็นก็ทำให้สุขภาพของ Ramanujan อ่อนแอลงและเมื่อเขากำลังจะตายเขาก็กลับบ้านไปอินเดีย
มันอยู่บนความตายของเขาในปี 1920 ว่าเขาอธิบายฟังก์ชั่นลึกลับที่เลียนแบบฟังก์ชั่น theta หรือรูปแบบแบบแยกส่วนในจดหมายถึง Hardy เช่นเดียวกับฟังก์ชั่นตรีโกณมิติเช่นไซน์และโคไซน์ฟังก์ชั่นเทต้ามีรูปแบบการทำซ้ำ แต่รูปแบบนั้นซับซ้อนและละเอียดอ่อนกว่าเส้นโค้งไซน์ง่าย ๆ ฟังก์ชั่น Theta ยังเป็น "super-symmetric" ซึ่งหมายความว่าหากฟังก์ชั่นทางคณิตศาสตร์ที่เฉพาะเจาะจงที่เรียกว่าการแปลง Moebius จะถูกนำไปใช้กับฟังก์ชั่นพวกเขาจะกลายเป็นตัวเอง เพราะพวกเขามีความสมมาตรฟังก์ชั่น theta เหล่านี้มีประโยชน์ในคณิตศาสตร์และฟิสิกส์หลายประเภทรวมถึงทฤษฎีสตริง
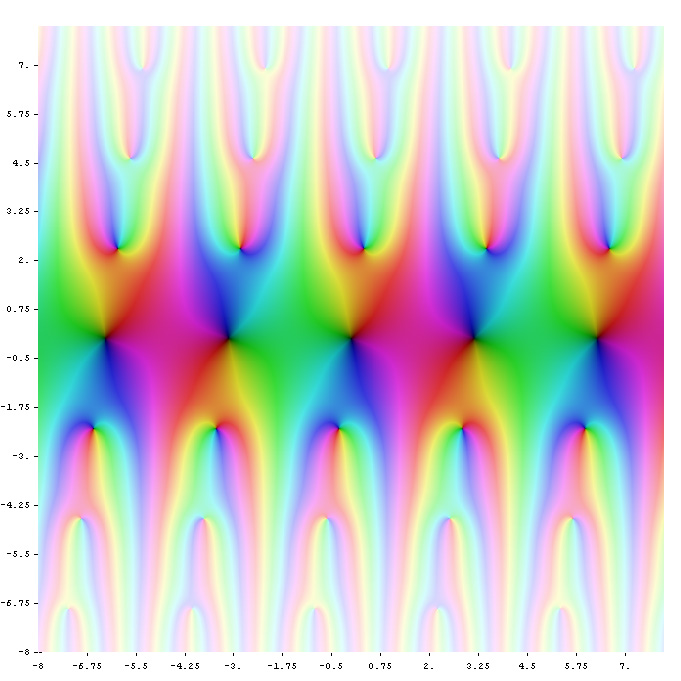
Ramanujan เชื่อว่า 17 ฟังก์ชั่นใหม่ที่เขาค้นพบคือ "รูปแบบโมดูลจำลอง" ที่ดูเหมือนฟังก์ชั่น theta เมื่อเขียนเป็นผลรวม infinte (ค่าสัมประสิทธิ์ของพวกเขามีขนาดใหญ่ในลักษณะเดียวกัน) Ramanujan, aฮินดูผู้ศรัทธาคิดว่ารูปแบบเหล่านี้ถูกเปิดเผยโดยเทพธิดา Namagiri
Ramanujan เสียชีวิตก่อนที่เขาจะพิสูจน์ลางสังหรณ์ของเขา แต่มากกว่า 90 ปีต่อมาโอโน่และทีมของเขาพิสูจน์ว่าฟังก์ชั่นเหล่านี้เลียนแบบรูปแบบโมดูลาร์ แต่อย่าแบ่งปันลักษณะที่กำหนดของพวกเขาเช่นความสมมาตรมาก
การขยายตัวของรูปแบบโมดูลจำลองช่วยให้นักฟิสิกส์คำนวณเอนโทรปีหรือระดับความผิดปกติ, ของรูดำ-
ในการพัฒนารูปแบบโมดูลาร์จำลอง Ramanujan เป็นทศวรรษก่อนเวลาของเขา Ono กล่าว; นักคณิตศาสตร์เท่านั้นที่คิดว่าสาขาคณิตศาสตร์เหล่านี้เป็นของสมการเหล่านี้เป็นของในปี 2545
“ มรดกของ Ramanujan มันกลับกลายเป็นว่ามีความสำคัญมากกว่าสิ่งที่ทุกคนจะเดาได้เมื่อ Ramanujan เสียชีวิต” Ono กล่าว
ผลการวิจัยได้ถูกนำเสนอเมื่อเดือนที่แล้วในการประชุม Ramanujan 125 ที่ University of Florida ก่อนครบรอบ 125 ปีของการเกิดของนักคณิตศาสตร์ในวันที่ 22 ธันวาคม
ติดตาม Livescience บน Twitter@livescience- เรายังอยู่ด้วยFacebook-Google+-