你知道整个数轴是相同尺寸作为包含在零和一之间的自身片段?
或者 1 + 1 – 1 + 1 – 1 + 1 – 1 + …到无穷大等于一半?
欢迎来到奇异的无限世界 - 一切都不像看上去的那样,有时根本没有答案可能是你能得到的最好答案。
和大卫·希尔伯特一起去度假
最著名的思想实验之一是由大卫希尔伯特设计的,他是一位传奇数学家,负责提出无穷大的奇异性,以帮助理解无穷大的奇异性。23 个问题这将定义 20 世纪的数学。它被称为希尔伯特大酒店,通常会这样像这样的东西:
想象一下您正在旅行,并且想要过夜。你终于找到一家酒店——方圆几英里内唯一一家——但可惜的是,你看到标牌上写着“无空房”。但是看,你需要某处睡觉,酒店看起来相当大,所以你决定进去要一个房间——以防万一。
“我们已经满了,”登记入住人员说,“房子里没有一个空闲房间。”
你失望地转身想走,却被她拦住了。
“等待!”她说。 “我们仍然可以让你入住——你看,这是一家特别特别的酒店。它有一个无限数量的房间。我们所要做的就是告诉已经入住酒店的每个人搬到隔壁房间!”
她按下按钮,对着对讲机讲话。
“这是一份客户公告,”她说。 “住在一号房间的客人必须搬到二号房间。二号房间的客人要搬进三号房间。三号房的客人请移至四号房,以此类推。”
她转身面向你,脸上带着微笑。
“我们开始吧,”她说。 “一号房间现在应该是空闲的。我给你办理入住。”

圆山大酒店:没有空房,但有适合每个人的空间
于是,你拿着钥匙转身离开,回自己的房间。但就在这时,你看到一群游客推门而入。
“嗨,”领队对店员说。 “我们有 20 个人,听说这个地方总能腾出空间容纳更多人。”
“没错,”店员回答道。 “让我来安排一些客人吧。”
她再次走向对讲机。
“又一个客户公告,”她说。 “我们酒店迎来了 20 位新客人。请大家搬到他们右边的 20 号房间:一号房间请搬到 21 号房间,二号房间请搬到 22 号房间,依此类推。谢谢你!”
她转身回到队伍中。
“这样应该就可以了!”她说着,将大家带入了 1 号至 20 号房间。

大巴抵达圆山大酒店
您必须承认,这位服务员给您留下了深刻的印象:她不费吹灰之力就成功地将 21 位新客人安置在一家满员的酒店里。但随后,电话铃响了,你看到她看起来很担心。
“你确定?是的,女士,我们——我们会看看我们能做些什么,”她说,然后挂断了电话。
“有一整辆载满旅客的巴士朝这边开来,”她告诉你。 “他们的数量无限多,而且他们都需要一张床过夜——我们需要将酒店的房间数量增加一倍才能容纳他们所有人!”
你们都想了一会儿如何解决这个招待噩梦,直到突然想到了这一点。
“我拿到了!”你告诉店员。 “只要把一号房的客人送到二号房,把二号房的客人送到四号房,把三号房的客人送到六号房,以此类推。如果每个客人都搬到两倍于当前房间号的房间,那么就会产生无限多个空位,车上的每个人都可以有一个房间!”
“天哪,你已经破解了,”店员喊道,再次打开了电信。 “为此,房间是免费的。”

那么,除了酒店工作人员作为一个职业被严重低估之外,希尔伯特酒店还告诉我们什么呢?从数学上来说,最大的教训是,我们所说的“无穷大”的表现与正常数字不同——也不应该如此。
数学中的无穷大
无限是——嗯,它的名字就是:无限。我们已经看到它如何不受常量相加或相乘的影响,但是如果我们想真正抽象一下怎么办?如果我们想求两个无穷大的和怎么办?像这样的东西:

嗯,从数学角度来说,这实际上很好。想一想:你有一个大得不可思议的东西,然后你把它加到其他大得不可思议的东西上——你会得到什么?

使用相同的推理,我们也可以将两个无穷大相乘。

但!如果我们想知道这个问题的答案怎么办:

或者这个:

嗯,这就是事情变得复杂的地方。让我们看看为什么。
无穷大有不同类型
无穷大是无穷大,但有些无穷大比其他无穷大。我知道,这听起来完全是胡说八道,但这是真的——事实上,你已经知道了。
希尔伯特旅馆向我们展示了思考无穷大的最简单方法:只要扑通扑通扑通扑通扑通扑通扑通扑通扑通扑通扑通扑通地沿着数轴往上走。这就是所谓的可数无穷大,这是最小的无穷大类型。
“可数无穷”这个词听起来有点矛盾——某物怎么可能是可数的和无限,对吧?但这个名字并不意味着你可以计算全部这个无限集合的成员的数量——它只是指有某种方法可以将它们放入列表中的想法。最明显的可数无限集是自然数,可以这样列出:

因此,在理解无穷大时,我们已经了解到一些重要的事情。请注意,我们谈论的是集合、集合成员和计数,而不是任何类似于数字的东西。看,在理解无穷大时,最大的误解之一就是将它视为一个非常非常大的数字——可以想象的最大数字。但事实并非如此。
你们中的一些人可能会说“当然这不是一个数字!”这就是为什么我们称其为“无穷大”,而不是,我不知道,两个或其他什么!”但陷入这个陷阱比你想象的更容易。毕竟,即使在大学水平的数学中,我们也经常被鼓励将无穷大视为一系列不断增加的数字的极限。
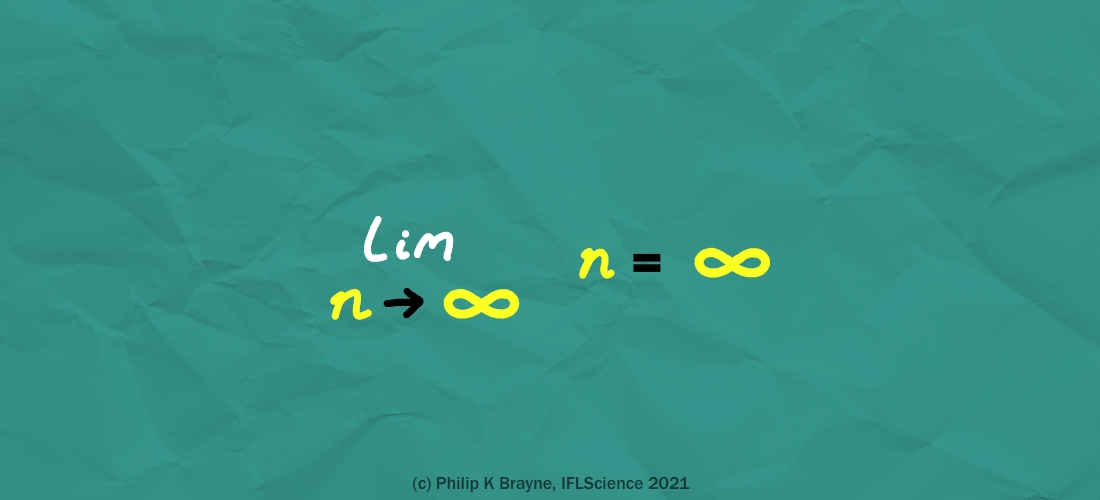
但无穷大是不是一个数字,但它的行为并不可靠——当我们尝试用它做数学时,这一点很快就会变得清楚。
无穷大减去无穷大等于什么?
我们已经看到自然数——一、二、三、四、五等等——形成了一个可数无限集合。事实上,任何与自然数一一对应的无限集——也就是说,任何你能想到一种合理的方式来列出从一到……好吧,从一开始的元素的无限集——都是相同:可数无限。例如,集合“偶数”是可数无限的,因为我们可以这样列出它们:

或者集合“整数”怎么样——你需要对此进行一些思考。

甚至“分数”也是可数的,尽管列出它们的方法是相当出乎意料的:

这就是希尔伯特酒店背后的逻辑:“酒店房间”的集合是可数的,因为(正如酒店房间的传统)它们是由自然数标记的。当客人都搬到更高的一个房间时,相当于给房间贴上这样的标签:

当他们搬到当前房间号两倍的房间时,我们可以将其视为这样标记:

但这里有一个问题:实数集怎么样?
如果您需要复习一下,实数是当有人说“想一个数字”时您会想到的任何数字。一、–72、?、log(14) – 如果您可以在数轴上指出它,那么它就是一个实数。通常,我们将实数写为十进制扩展,但这有助于我们列出它们吗?
让我们让自己的生活变得轻松一些,只列出零或以上的实数。列表中的第一个数字很简单:

但接下来会发生什么呢? 1? 0.1? 0.000001?还有别的事吗?
事实证明,实数根本无法像自然数或整数一样放入列表中。用数学术语来说,它们是:不可数无限。并且不可数无穷大于可数无穷。事实上,要大得多。

因此,这为我们之前的问题提供了答案——至少是部分答案。只要我们遵守某些特定要求,我们就可以取无穷大之差。例如我们可以说:

但至于

嗯,它可以等于一:

或者两个:

或负 pi:

实际上根本没有好的答案——我们被困住了! (在数学中,我们称此类表达式为“未定义”,这使得整个情况不再那么尴尬。)
思考像数学家一样感到困惑
如果你还没有因为这一切而感到头痛,那么好消息是:我们基本上刚刚触及了无限怪异的表面。但在我们暂时结束之前,让我问你一件事:你能想到可数无穷大和不可数无穷大之间的集合吗?
任何事物?
顺便说一句,这是一个真正的问题——没有人知道答案。这个问题——是否存在任何大小大于自然数但小于实数的集合——被称为连续假设,而且它一直坐在那里未经证实,嘲笑逻辑学家,至今已近 150 年。与黎曼假设或者P 与 NP,这也不是那些“未经证实但每个人基本上都认为这是真的”的假设之一——数学家们真正的分裂关于这个问题。
问题以及我们不太可能很快找到解决方案的原因是连续统假设是无法证明的。
这并不是夸张:使用我们目前拥有的数学工具,无论如何都不可能证明连续统假设。这听起来很奇怪,对吧?如何才能确定一个假设无法证明– 并不是说现在对任何人来说都太困难了,而是即使是地球上最聪明的人,可以访问人类已知的每一条信息,也永远无法找到解决方案?
嗯,这并不容易,这是肯定的。为了证明这一不可证明性,两位世界著名的数学家花了三十多年的时间涉足了数学中最抽象、最深奥的领域之一。我们不打算在这里详细讨论,因为我们没有 33 年的时间来解释它,但 CliffsNotes 版本是这样的:

换句话说,我们无法证明它不是真的,我们也无法证明它是真的,让我们结束这一切吧。
我知道这并不令人满意,但这里仍然有一个教训值得我们学习:无论您可能会发现无穷大的概念令人困惑,至少要知道您并不孤单。因为当谈到无穷大时,对于世界上最伟大的两位数学家来说,“好吧,我猜我们永远不会知道!”曾经是一个好人——不,是一个伟大的- 结果。









