你知道整個數軸是相同尺寸作為包含在零和一之間的自身片段?
或 1 + 1 – 1 + 1 – 1 + 1 – 1 + …到無窮大等於一半?
歡迎來到奇異的無限世界 - 一切都不像看起來的那樣,有時根本沒有答案可能是你能得到的最好答案。
和大衛希爾伯特一起去度假
最著名的思想實驗之一是由大衛希爾伯特設計的,他是一位傳奇數學家,負責提出無窮大的奇異性,以幫助理解無窮大的奇異性。23 個問題這將定義 20 世紀的數學。它被稱為希爾伯特大飯店,通常會這樣像這樣的東西:
想像一下您正在旅行,並且想要過夜。你終於找到一家旅館——方圓幾英里內唯一一家——但可惜的是,你看到標誌上寫著「無空房」。但是看,你需要某處睡覺,酒店看起來相當大,所以你決定進去要一個房間——以防萬一。
“我們已經滿了,”登記入住人員說,“房子裡沒有一個空房間。”
你失望地轉身想走,卻被她攔住了。
“等待!”她說。 「我們仍然可以讓你入住——你看,這是一家特別特別的酒店。它有一個無限數量的房間。我們所要做的就是告訴已經入住酒店的每個人搬到隔壁房間!
她按下按鈕,對著對講機講話。
“這是一份客戶公告,”她說。 「住在一號房間的客人必須搬到二號房間。二號房間的客人要搬進三號房間。三號房的客人請移至四號房,以此類推。
她轉身面向你,臉上帶著微笑。
「我們開始吧,」她說。 「一號房間現在應該是空閒的。我給你辦理入住。

圓山大飯店:沒有空房,但有適合每個人的空間
於是,你拿著鑰匙轉身離開,回自己的房間。但就在這時,你看到一群遊客推門而入。
「嗨,」領隊對店員說。 “我們有 20 個人,聽說這個地方總是能騰出空間容納更多人。”
「沒錯,」店員回答。 “讓我來安排一些客人。”
她再次走向對講機。
「又一個客戶公告,」她說。 「我們飯店迎來了 20 位新客人。請大家搬到他們右邊的 20 號房間:一號房間請搬到 21 號房間,二號房間請搬到 22 號房間,依此類推。謝謝你!
她轉身回到隊伍中。
“這樣就可以了!”她說著,將大家帶入了 1 號至 20 號房間。

巴士抵達圓山大飯店
您必須承認,這位服務員給您留下了深刻的印象:她不費吹灰之力就成功地將 21 位新客人安置在滿員的酒店裡。但隨後,電話鈴響了,你看到她看起來很擔心。
「你確定?是的,女士,我們——我們會看看我們能做些什麼,」她說,然後掛斷了電話。
「有一整輛載滿旅客的巴士朝這邊開來,」她告訴你。 “他們的數量無限多,而且他們都需要一張床過夜——我們需要將酒店的房間數量增加一倍才能容納他們所有人!”
你們都想了一會兒如何解決這個招待噩夢,直到突然想到了這一點。
“我拿到了!”你告訴店員。 「只要把一號房的客人送到二號房,把二號房的客人送到四號房,把三號房的客人送到六號房,以此類推。如果每個客人都搬到兩倍於當前房間號的房間,那麼就會產生無限多個空位,車上的每個人都可以有一個房間! ”
「天哪,你已經破解了,」店員喊道,再次打開了電信。 “為此,房間是免費的。”

那麼,除了酒店工作人員作為一個職業被嚴重低估之外,希爾伯特酒店還告訴我們什麼呢?從數學上來說,最大的教訓是,我們所說的「無窮大」的表現與正常數字不同——也不應該如此。
數學中的無窮大
無限是──嗯,它的名字就是:無限。我們已經看到它如何不受常量相加或相乘的影響,但是如果我們想真正抽像一下呢?如果我們想求兩個無窮大的和怎麼辦?像這樣的東西:

嗯,從數學角度來說,這實際上很好。想想看:你有一個大得不可思議的東西,然後你把它加到其他大得不可思議的東西上——你會得到什麼?

使用相同的推理,我們也可以將兩個無窮大相乘。

但!如果我們想知道這個問題的答案怎麼辦:

或者這個:

嗯,這就是事情變得複雜的地方。讓我們看看為什麼。
無窮大有不同類型
無窮大是無窮大,但有些無窮大比其他無窮大。我知道,這聽起來完全是胡說八道,但這是真的——事實上,你已經知道了。
希爾伯特旅館向我們展示了思考無限大的最簡單方法:只要撲通撲通撲通撲通撲通撲通撲通撲通撲通撲通撲通地沿著數軸往上走。這就是所謂的可數無窮大,這是最小的無窮大類型。
「可數無窮」這個詞聽起來有點矛盾——某物怎麼可能是可數的和無限,對吧?但這個名字並不代表你可以計算全部這個無限集合的成員的數量——它只是指有某種方法可以將它們放入列表中的想法。最明顯的可數無限集合是自然數,可以這樣列出:

因此,在理解無窮大時,我們已經了解到一些重要的事情。請注意,我們談論的是集合、集合成員和計數,而不是任何類似數字的東西。看,在理解無窮大時,最大的誤解之一就是將它視為一個非常非常大的數字——可以想像的最大數字。但事實並非如此。
你們中的一些人可能會說“當然這不是一個數字!”這就是為什麼我們稱其為“無窮大”,而不是,我不知道,兩個或其他什麼! ”但陷入這個陷阱比你想像的更容易。畢竟,即使在大學程度的數學中,我們也經常被鼓勵將無窮大視為一系列不斷增加的數字的極限。
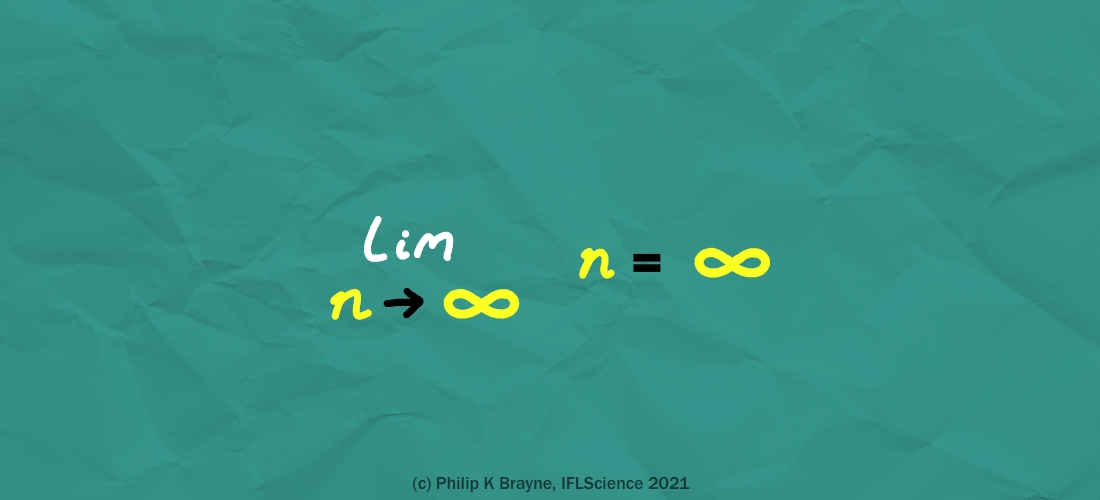
但無窮大是不是一個數字,但它的行為並不可靠——當我們嘗試用它做數學時,這很快就會變得清楚。
無窮大減去無窮大等於什麼?
我們已經看到自然數——一、二、三、四、五等等——形成了一個可數無限集合。事實上,任何與自然數一一對應的無限集合——也就是說,任何你能想到一種合理的方式來列出從一到……好吧,從一開始的元素的無限集合——都是相同:可數無限。例如,集合“偶數”是可數無限的,因為我們可以這樣列出它們:

或者集合「整數」怎麼樣——你需要對此進行一些思考。

甚至「分數」也是可數的,儘管列出它們的方法是相當出乎意料的:

這就是希爾伯特酒店背後的邏輯:「酒店房間」的集合是可數的,因為(正如酒店房間的傳統)它們是由自然數標記的。當客人都搬到更高的一個房間時,相當於給房間貼上這樣的標籤:

當他們搬到目前房間號碼兩倍的房間時,我們可以將其視為這樣標記:

但這裡有個問題:實數集怎麼樣?
如果您需要複習一下,實數是當有人說「想一個數字」時您會想到的任何數字。一、–72、?、log(14) – 如果您可以在數軸上指出它,那麼它就是一個實數。通常,我們將實數寫成十進制擴展,但這有助於我們列出它們嗎?
讓我們讓自己的生活變得輕鬆一些,只列出零或以上的實數。清單中的第一個數字很簡單:

但接下來會發生什麼事呢? 1? 0.1? 0.000001?還有別的事嗎?
事實證明,實數根本無法像自然數或整數一樣放入列表中。用數學術語來說,它們是:不可數無限。且不可數無窮大於可數無窮。事實上,要大得多。

因此,這為我們之前的問題提供了答案——至少是部分答案。只要滿足某些特定要求,我們就可以取無窮大之差。例如我們可以說:

但至於

嗯,它可以等於一:

或兩個:

或負 pi:

實際上根本沒有好的答案——我們被困住了! (在數學中,我們稱此類表達式為“未定義”,這使得整個情況不再那麼尷尬。)
思考像數學家一樣感到困惑
如果你還沒有因為這一切而感到頭痛,那麼好消息是:我們基本上剛剛觸及了無限怪異的表面。但在我們暫時結束之前,讓我問你一件事:你能想到可數無窮大和不可數無窮大之間的集合嗎?
任何事物?
順便說一句,這是一個真正的問題——沒有人知道答案。這個問題——是否存在任何大小大於自然數但小於實數的集合——被稱為連續假設,而且它一直坐在那裡未經證實,嘲笑邏輯學家,至今已近 150 年。與黎曼假設或者P 與 NP,這也不是那些「未經證實但每個人基本上都認為這是真的」的假設之一——數學家們真正的分裂關於這個問題。
問題以及我們不太可能很快找到解決方案的原因是連續統假設是無法證明的。
這並不是誇張:使用我們目前擁有的數學工具,無論如何都不可能證明連續統假設。這聽起來很奇怪,對吧?如何才能確定一個假設無法證明– 並不是說現在對任何人來說都太困難了,而是即使是地球上最聰明的人,可以訪問人類已知的每一條信息,也永遠無法找到解決方案?
嗯,這並不容易,這是肯定的。為了證明這一不可證明性,兩位世界著名的數學家花了三十多年的時間涉足了數學中最抽象、最深奧的領域之一。我們不打算在這裡詳細討論,因為我們沒有 33 年的時間來解釋它,但 CliffsNotes 版本是這樣的:

換句話說,我們無法證明它不是真的,我們也無法證明它是真的,讓我們結束這一切吧。
我知道這並不令人滿意,但這裡仍然有一個教訓值得我們學習:無論您可能會發現無窮大的概念令人困惑,至少要知道您並不孤單。因為當談到無窮大時,對於世界上最偉大的兩位數學家來說,“好吧,我猜我們永遠不會知道!”曾經是個好人——不,是一個偉大的- 結果。









