简介

诺贝尔奖冠军欧内斯特·卢瑟福(Ernest Rutherford)曾经说过:“所有科学都是物理或邮票收集。” (具有讽刺意味的是,卢瑟福(Rutherford)赢得了他的诺贝尔(Nobel)化学,而不是物理学)。物理学家可能不是那里最谦虚的人,但是如果他们擅长一件事,那就想出自己的想法名称。这是一些最命名的物理东西,以及它的含义。
奥斯特瓦尔德成熟

想象一下在上面有冷凝的表面,就像密封的水瓶一样。起初,冷凝水是许多微小水滴的形式。但是,如果您在不打扰的情况下将那瓶水留一段时间,您会注意到所有这些小滴开始变得越来越大。您正在观察物理学家所说的Ostwald成熟。
基本的前提是,较大的液滴比较小的液滴更“有益”。这是因为液滴表面的颗粒比中间的颗粒稳定,而小滴在表面上的分子比大颗粒比大颗粒更大。为了变得更稳定,小孩子们结束了团结起来,形成了更大的液滴。因此,如果您将那个水瓶留长时间,则可以观看那些小滴结合并变得越来越大。
即使您从来没有花时间盯着水杯上的滴水,如果您曾经在冰箱里放冰淇淋太久,奥斯特瓦尔德就会成熟。曾经是美味的岩石道路的那条脆脆的冰冷的团块经历了奥斯特瓦尔德(Ostwald)的成熟。冰淇淋中的晶体从小到大,最终产生了那些冰冷的簇。
冯·卡曼沃特克斯街
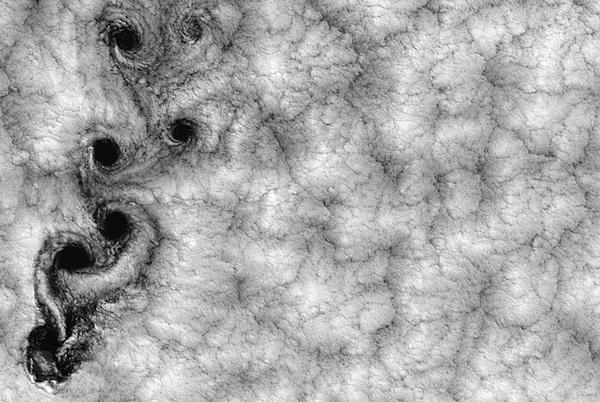
在流体力学领域,物理学家看着流体通过太空的流动及其制造的模式。他们研究的更美丽的图案之一是漩涡和漩涡式漩涡,诸如船只在他们身后留下的东西。当船在水中移动时,将液体切成两半。随着船后的水团聚,它创造了一种交替的涡流模式,称为von Karman Vortex街。
该现象对各种问题都很重要。例如,高大的建筑物,烟囱和潜艇潜望镜都必须应对周围的风。随着风的流逝,然后向后圈,力会导致这些结构有力振动。某些结构,例如天线和潜望镜,有鳍可以降低风,并防止两侧的涡流开会。
而且,不仅要处理涡流街的大事。当昆虫击败翅膀时,它们在空中产生微小的涡流。但是,昆虫没有接受漩涡可以产生的阻力,而是在上风前有点扭动翅膀,以便他们的翅膀随着空气旋转的空气而向上抬起。
tachyonic抗纤维

想向过去发送消息吗?没问题,只需拉出您的速旋抗纤维。至少在1907年,当艾伯特·爱因斯坦(Albert Einstein)考虑将比光信号快于过去发送的速度时,至少在1907年真正始于1907年。但是爱因斯坦并没有将其称为速旋抗thitephone。正是格雷戈里·本福德(Gregory Benford)于1970年首次创造了这句话。这是许多这样的悖论之一,本福德总结了这样的悖论:
假设爱丽丝和鲍勃签订了以下协议:当且仅当她一点点不从他那里收到一封时,爱丽丝将在三点钟向鲍勃发送消息。在两点钟收到爱丽丝的消息后,鲍勃立即将消息及时发送回消息,以在一个钟点到达爱丽丝。但是,只有在不进行第一次交换的情况下,第二次交换将发生。
速旋抗纤维需要在理论上甚至不存在的“ tachyon颗粒”,更不用说实践了。
毛茸茸的球定理

您是否曾经尝试过梳理椰子?任何物理学家都会告诉你不要。但是他们真正在说的是拓扑。
如果您的头发覆盖了所有长度相同的头发,那么就无法将它们梳理到所有的表面上都很好地躺着。想想一个网球,头发的头部。如果您尝试将它们全部梳理,那么您将在某个地方的牛皮上结束,然后总是用一个小的秃头开始刷牙。
从旋风到计算机图形,这将应用于许多事情。纳米技术工程师使用该定理制作了微小的金发,可以彼此粘住。而且,由于风就像一束头发在地球上扫过,所以总会有一个地球上的一个地方,空气仍然是您开始刷牙的秃头。
巨大的定理

这是指从字面上看巨大的定理。该巨大的定理也被称为有限简单组的分类,占据了100多位数学家,数百篇期刊文章和15,000页,以证明它是有史以来最大的数学证明。
那些数学家在巨大的定理中列出的是,每个有限的简单数字属于四个类别之一:环状,交替,简单的谎言类型或零星。对这四个小组的研究一直始于1832年,直到2004年才完成。世界上只有少数数学家完全了解证据,甚至不清楚从完成的数学可能会增加什么数学。除了世界纪录。