当音乐家弹奏吉他时,弦乐的振动会产生人耳朵作为音乐所听到的声波。当拨出吉他弦时,它会移动一定距离,具体取决于吉他弹手的难度。字符串返回其起点,并在相反方向上行驶几乎相同的距离。弦的振动能以声音的形式消散。这会导致字符串移动的距离或振动的幅度逐渐减小。声音的音量逐渐消失,直到弦最终保持沉默。
吉他弦是简单的谐波运动或SHM的一个示例。 SHM可以在整个大自然中看到。它描述了原子的振动,巨星的变异性以及从乐器到摇摆摩天大楼的无数其他系统。
普林斯顿大学的WordNet将简单的谐波运动定义为“恢复力与位移成正比的周期性运动”。周期性意味着运动以恒定,可预测的速度重复。关于恢复力与位移成正比的部分仅意味着您越努力推出东西,它就越难推动。
SHM还描述了从春天悬挂的球的运动。根据佐治亚州立大学的说法,球受到线性弹性恢复力的约束高物理学网站。在图上绘制,随着时间的推移,球的上下运动可以说为平滑,重复的振荡或正弦波。可以使用胡克定律计算波的形状。
罗伯特·胡克(Robert Hooke)是一位英国科学家,数学家和建筑师,对从天文学到微生物学的许多方面都感兴趣。根据放大镜下的物体,他是第一个使用“细胞”一词来描述植物组织的成分的人。物理超文本。他还研究了时钟和计时,并在1675年开发了一种弹性或弹性的理论,以调节摆钟。简而言之,该理论说:“扩展与武力成正比。”
从数学上讲,胡克定律表示为f = - kx,其中f是力,x是春季放松或原始长度的长度变化,k是指定拉伸或压缩一定距离所需的力量的特征弹簧常数。负符号表明恢复力是位移的相反方向。
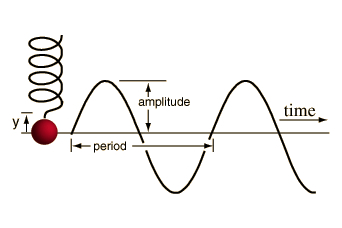
循环运动
根据循环运动和简单的谐波运动之间的联系波士顿大学。考虑磁盘边缘上的一个点,因为它以逆时针旋转以固定轴周围的恒定速率旋转。如果我们仅在磁盘转动时绘制点的垂直位置,则会产生正弦图。如果我们在弹簧上绘制质量的位置,以简单的谐波运动随时间的函数绘制质量的位置,这与我们所获得的图形完全相同。
摆
简单的摆的行为就像弹簧等谐波振荡器一样。但是,摆的周期不是由其质量而是由其长度确定。另一个重要的区别是,对于摆的情况,恢复力不是由弹簧而是由重力提供。由于重力是在垂直向下拉动摆,而不是沿着运动的相反方向向后拉,因此恢复力是一种复杂的三角函数。然而,摆板几乎近似于简单的谐波运动,只要它们与休息点不超过几个程度。
抑制谐波运动
所有机械系统均受阻尼力,这会导致运动的幅度随着时间的流逝而减小。这些力可以包括运动部位,空气阻力或内部力量(例如弹簧中的内力)之间的摩擦力,这些力倾向于将能量耗散为热量。
根据简单的谐波运动,阻尼力通常与振荡质量的速度成正比。纽约州立大学石溪。这种力最终将使一个振荡系统停止,如果足够好,它实际上可以在振荡开始之前停止振荡。
弹簧弹跳的重量将继续弹跳很长时间,但不是永远的。金属弹簧中的空气阻力和内部电阻最终将消散系统的动能并将其停止。但是,如果将重量悬浮在冷糖蜜锅中,并且弹簧被拉伸并释放,则重量可能只能缓慢返回其休息位置,而不会在其上方弹跳一次。我们认为,空气中的重量弹跳不足,并且重量在糖蜜中缓慢移动,甚至从未弹过一次以使其被阻尼。如果该系统正好在这两个条件之间的尖峰上,则据说它会受到严重抑制。
“我们知道,实际上,春天不会永远振荡。摩擦力将减少振荡的振幅,直到最终系统处于静止状态。”加利福尼亚大学圣克鲁斯分校。不足的振荡器的振幅经历了指数衰减,这意味着在一定时间后,振荡的幅度将减少一半,并且在同一时间段后,它将再次减少一半。一个熟悉的例子是钟声的腐烂声。
在许多情况下,需要阻尼以防止不受控制的弹跳。也许最熟悉的例子是汽车悬架系统。车轮安装在弹簧上,因此它们可以响应在汽车的尸体相对较高时在道路上的颠簸和下降而上下移动。但是,如果没有阻尼,汽车将无法控制地上下跳动。为了防止这种情况,汽车具有冲击吸收器,可以通过向悬架系统添加摩擦力来抑制弹簧的运动。
驱动的谐波运动
当期望谐波运动持续存在时,抑制是一个必须通过驱动力克服的问题。考虑祖父时钟中的摆。在每个方向上的最远点,逃脱机制由缓慢下降的重量的重力能力提供动力,使摆会带来一个微小的轻推,足以克服机械摩擦和空气阻力的阻尼效应并保持摆锤的运动。
驱动谐波运动的一种表现是耦合共振,或同情振动。这是一个振动,它是由相邻体中完全相同的振动在一个体内产生的。一个熟悉的例子是一个游乐场秋千。如果它具有相同长度的两个波动,则在一个秋千上摇摆可能会导致另一个挥杆动作开始移动。这样做的原因是,第一个秋千会导致支撑横条在每个周期中向前稍微向前移动。尽管这种运动通常很小,因为秋千的长度相同,但它们的谐振频率将相同,因此横杆的微小运动提供的驱动力被放大,从而导致第二个秋千明显移动。谐波振荡器以其谐振频率驱动的另一个例子是电吉他通过允许放大声音的反馈来驱动弦的持续振动,可以无限期地维持音符。
但是,有时候,驱动力下的谐波运动可能是有害的,甚至可能是灾难性的。如果以大于阻尼力的速率以自然或谐振系统的自然或谐振频率施加这种力,则可以消散能量,“……相对较小的驱动力可以累积到较大的振幅振荡,仅仅是因为能量继续以正确的频率注入到适当的频率中。”波士顿大学。这意味着,如果阻尼不足的系统是由外力以其谐振频率驱动的,则运动的幅度可以增加,直到系统失败为止。最戏剧性的例子之一就是1940 Tacoma Narrows Bridge崩溃。强烈的持续风驱动了桥甲板的振荡,该甲板的振幅增加了,直到破裂为止。谐波运动被驱动到失败点的另一个例子是歌手可以打碎酒杯通过以谐振频率唱出音符。
现实生活中的谐波运动很少很简单。当我们查看实际的宏观振荡系统时,可能会有任何数字混淆变量,例如温度和气压波动或机械零件上的磨损,这可能会影响运动的振幅和周期。但是,通过假设机械系统是简单的谐波运动,我们通常可以对这些系统的行为方式进行适当的准确近似。
其他资源