在将近40年的时间里,一个简单的小假设一直悄悄地坐在图理论的一角,注意自己的业务。它被称为“掩体猜想”,它似乎总是很自觉 - 当然,没有人可以证明它,但这很有意义 - 当然,没有人找到反例。
到目前为止。几乎每个人都感到惊讶,一群数学家宣布上个月发表一篇论文,他们声称这证明了猜想是错误的。目前,该论文目前在Arxiv预印服务器上发布,因此尚未经过同行评审,但仍在数学世界中引起了波浪,不仅是为了证明本身,而且是为了对数学作为整个学科所说的话。
猜想
首先是由物理学家Pieter Kasteleyn提出的1985年给同事,床床的猜想实际上与床根本没有任何关系。相反,它涉及图形 - 除非您是工作数学家,否则可能不是您现在正在考虑的那种图表。
“一张图由一堆顶点和一堆连接顶点的边缘,”维多利亚大学数学和统计系的助理教授Trefor Bazett解释说。最近的YouTube视频关于证明。
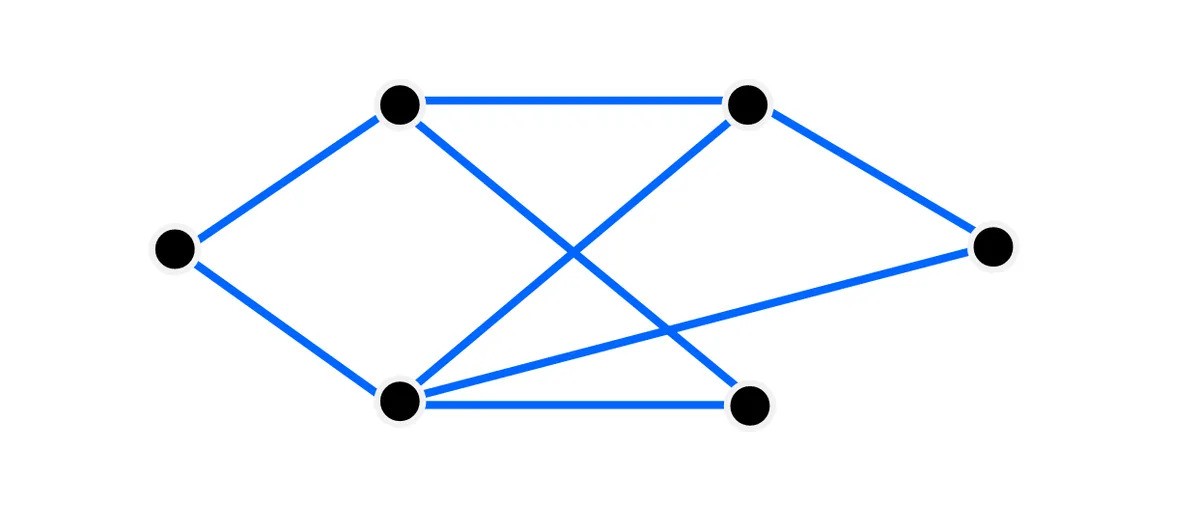
一个具有六个顶点和八个边缘的图形。
图片来源:Iflscience
“您可以想象,也许社交网络中的人们,”他建议,“然后联系是你是朋友。”
精确地将此图进行加倍,您可以创建所谓的铺位图:彼此顶部的两个相同的图,并由“帖子”连接。看,一旦亲自看到它,您就会理解所有主题术语。
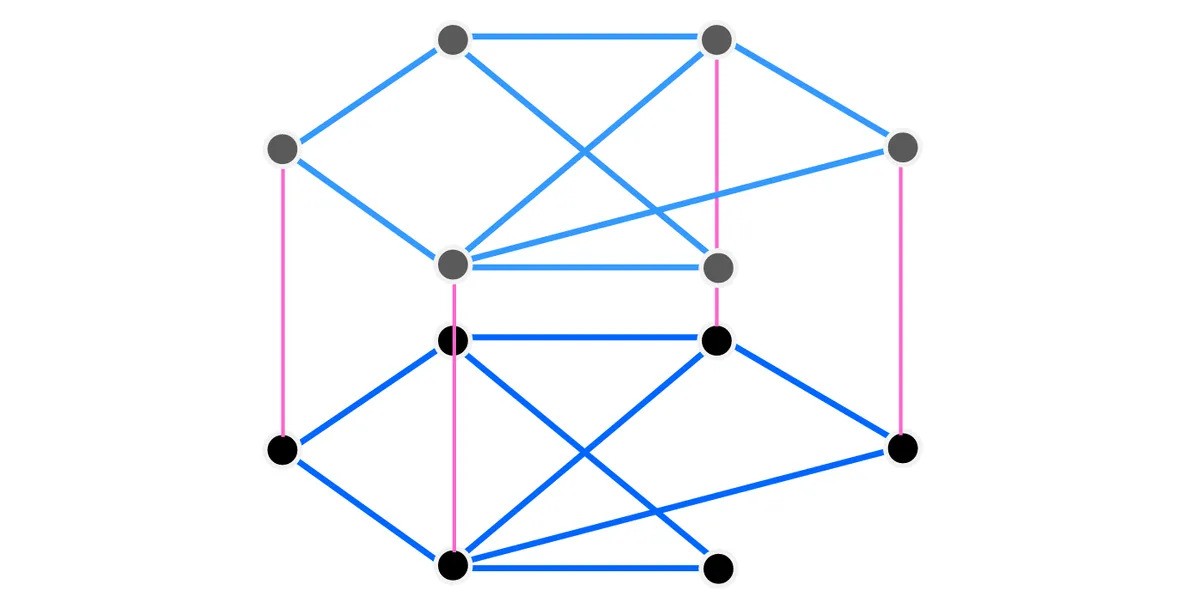
同一张图中铺在铺位地层中。这些粉红色的顶点称为床柱。
图片来源:Iflscience
因此,我们拥有我们的设置 - 我们之间的友谊,或者在街道连接的地图上的位置,或者您想象的图表所代表的任何东西。现在,我们将考虑如何通过图本身进行移动 - 因此,假设您想从点到你指出v在上面的图中,我们有以下选项:
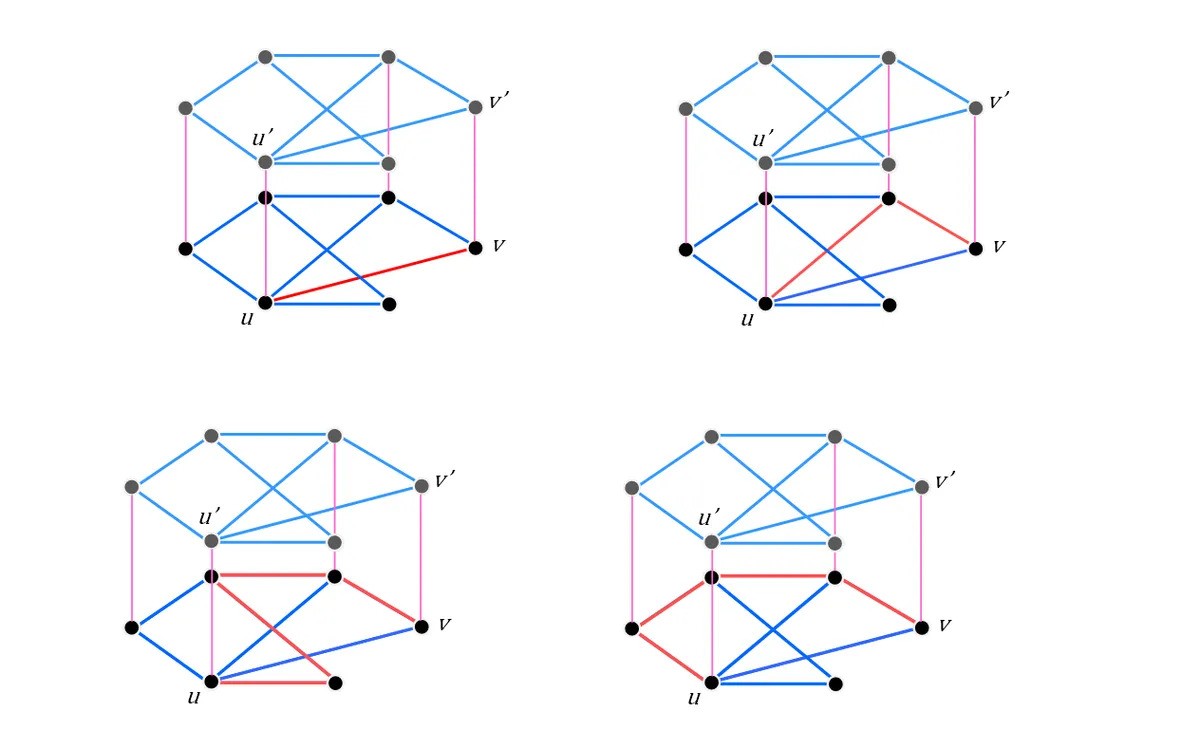
从你到v以红色突出显示。
图片来源:Iflscience
到目前为止和我们在一起?太好了,因为这是事情变得更加复杂。我们现在要做的是删除一些边缘 - 失去朋友;无论您喜欢什么,都可以挡住街道 - 看看我们仍然可以从中获得的可能性你到v之后。
因此,有了所有背景,我们现在就可以谈到床床的猜想的陈述,这就是:p((你↔v)≥p((你↔v')。
“它说我可以从中获得的概率你到v- 也就是说,我可以沿基地移动的概率 - 更大或等于我可以在基地中启动的概率,然后到达v'[…]在顶部铺位上,” Bazett解释说。
“猜想说这对于所有连接的图以及所有床柱的子集都是正确的,所有对你和v。”
从直觉上讲,这是有道理的:当然,与您的起点相同的端点要比需要您的起点同样的端点更容易。尝试一些示例只会加强信念 - 除非,否则您愿意用几千个顶点和边缘构建图形。
证明
通常,在数学中,反驳假设比证明这一点要容易。毕竟,要证明某些东西,您必须在所有情况下都表明每个可能的例子是正确的 - 反驳它只需要找到一个反例。
床床的猜想的问题是 - 好吧,没有人在寻找反例。 “如果猜想这么明显是真的,为什么要寻找反例?”加州大学洛杉矶分校的数学教授,新论文的作者之一伊戈尔·帕克(Igor Pak)博客文章突破。
“好吧,因为你总是应该这样做,”他反驳。 “对于任何猜想。特别是如果其他所有人都这样当然,如毫无疑问是完全确定的,猜想是真的。”
现在,是2020年代;你知道这些天是如何完成数学的,帕克也是如此。他写道:“我们从无数的计算机实验开始尝试所有小图。” “当这些失败时,我们尝试使用AI和其他计算机辅助工具。”
即便如此,似乎还没有反示例即将到来 - 团队开始担心,即使有人出现,也不足以完全反驳这一猜想。在此时,神经网络采样的图是如此之大,以至于计算相关概率确切地将是不可能的,因此任何证据充其量都是99.9999%的肯定是正确的。
但是,尽管“ 99.99%的信心[…]可能是核物理学的黄金标准,”帕克写道,“数学期刊往往更喜欢100%的正确性。”
“大多数期刊都会拒绝考虑一个五个Sigma反例',”他补充说。
因此,与其坚持不懈地没有果实的机器学习技巧,即使成功,他们的结果也可能无法接受,而是退后一步。然后,在今年6月,纸击中改变一切的arxiv。
“我在晚上找到了,直到凌晨3点,我都读了它,”帕克的研究生之一,一位纸的合着者尼基塔·格拉德科夫(Nikita Gladkov)告诉量子。 “我当时想,'哇,这太疯狂了。绝对令人难以置信。'”
这不是掩盖猜想的证明,但它是近距离的 - 陈述的表述,该语句处理了称为HyperGraphs的对象,而不是图形。作者,剑桥大学的研究生和有成就的Googoloks名字叫劳伦斯·霍洛姆(Lawrence Hollom),表明在这些物体中,床床的猜想是……错误。
霍洛姆(Hollom)提出了自己的作品,以试图概括铺位的猜想,或者,事实证明,这表明它不能被概括。最终,正是他的论文激发了原始猜想的证明。
通过转换Hollom的HyperGraph,该团队创建了一个图形,可以反驳床床的猜想。它绝对是可怕的 - 7,222个顶点,通过14,442个边缘连接 - 相关概率的差异是微小的:“天文学小”,帕克写道:“按照-10的顺序-6500。”
他补充说:“但这是负面的,这就是我们所需要的。”猜想是正式错误的。
结果
那么,这是什么意思,除了显而易见吗?好吧,有些失望,特别是对于应用数学家和物理学家而言:如果床头箱的猜想是正确的,它将验证一个关于流体如何通过固体传播的假设,并授予研究渗透物理学的研究人员。
但不仅如此,突破性的道德影响。未来的数学家是否应该更愿意接受概率证明?他们会尽可能有效或完整吗?
普林斯顿的数学教授诺加·阿隆(Noga Alon)告诉Quanta:“这是一个哲学问题。” “我们如何查看仅具有高可能性的证据?”
他说:“也许概率证明会使您对真正发生的事情的了解或直觉更少。”
最后,这是对数学家的警告,不要因为喜欢它而接受猜想。阿隆说:“我们必须怀疑,即使是直觉上看起来很可能是真实的事情,”
这是巴克长期以来一直拥护的情绪。他告诉Quanta:“有些猜想是出于实质的动机,而其他猜想是由一厢情愿的动机。”
似乎是后者的猜想。
尚未在同行评审的纸上可以找到arxiv。









