淫荡的兔子和迷幻的分形有什么共同点？逻辑图

分形在数学中占据着一个奇怪的位置。它们是抽象的量子领域的窗口位于二维和三维之间，声称可以证明英国海岸线是无限长尽管任何地图都会告诉你事实并非如此……但它们也出奇地实用。以曼德布洛特集为例：

你可能以前见过这种图案，但你有没有想过它到底意味着什么？尽管曼德布洛特集看起来迷幻，但它与我们周围的世界有着深刻的联系——这一切都归结于一组数学方程，统称为物流图。

什么是物流地图？

逻辑斯蒂映射在数学界很有名。它起源于 19 世纪上半叶，是一种模拟人口动态的方法，但它已经演变成一个最好的例子，说明随机混乱是如何从看似简单的起点产生的。从数学上讲，它看起来像这样：

用英语来说，意思是“通过将当前数字乘以某个常数，可以得到序列中的下一个数字r和一减它自己”，所以......实际上，你知道吗——也许举个例子会更容易理解。

让我们选择作为起点X₀= 1/2（我们总是选择一个介于 0 和 1 之间的值作为我们的起点，1/2 是合适的，也是中心值），我们将设置r成为[旋转轮盘] 3.然后地图会给我们

另一方面，如果我们设定r= 2.5 我们得到

如果我们增加r最高可达 3.5

请记住，逻辑斯蒂地图最初是用来模拟种群动态的，这是一种很好的思考方式。假设我们正在模拟一群兔子如何随时间变化：那么逻辑斯蒂地图告诉我们，明天我们有多少只兔子取决于我们今天有多少只兔子以及繁殖率兔子数量——它们繁殖新兔子的速度有多快。兔子越多，繁殖的兔子就越多，所以我们将繁殖率乘以当前兔子数量，X_n。但如果兔子太多，食物就会耗尽，一些兔子将被迫离开（或饿死）。这就是（1 -X_n）来自——它反映了这样一个事实：一座山上能生活的兔子数量是有限的，否则它们就会变得过于成功，不利于他们自己。

逻辑图虽然表面上很简单，但它给了我们一个出奇的好预测现实世界中观察到的种群动态。换句话说，上面的图表是使用纯数学获得的，但在适当的情况下（特别是与兔子口渴有关的情况），它们看起来与现实世界中兔子种群的数据非常相似。

好的，很棒，但是这与曼德布洛特集合有什么关系？

好吧，忘掉X值，并将逻辑映射视为r。不久之后，您就会开始发现一些奇怪的行为。

让我们从r= 0。在零和一之间，逻辑映射注定会逐渐消失。

图像改变时r达到 1。在 1 到 3 之间，逻辑图会带你到达一个特定的值，无论你选择什么作为起点。有时它会很快到达那里，有时很慢，有时它会在到达那里之前稍微摆动一下，但它总是会到达同一点（对于观众中的书呆子来说，这等于 1-1/r）。

但在r= 3，有趣的事情发生了：逻辑图开始振荡。基本上，您得到的值开始在两个固定点之间跳跃。

这种情况持续到你到达r? 3.44949（准确形式，r=1 + ?6)，当你开始看到四个固定点时。

然后在r? 3.54409，这种情况会再次发生，然后一次又一次，链中的值数量每次都会翻倍。这种情况会一直持续，直到达到神奇的数字：r? 3.56995，这时一切都......崩溃了。

现在到了非常酷的部分：如果我们绘制一个图表r反对X_n，让X_n增加，我们得到：

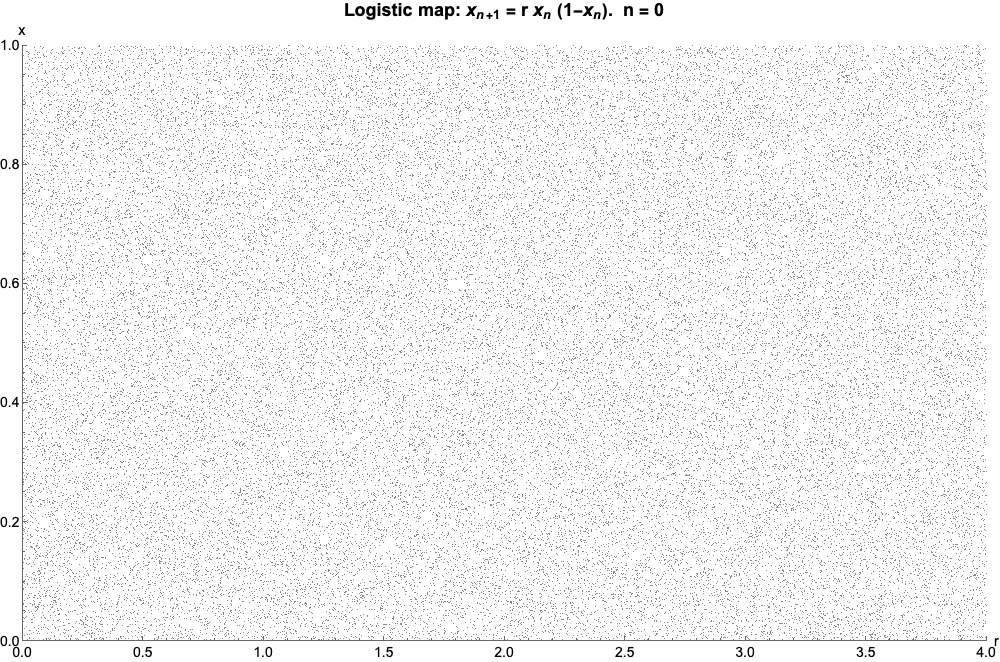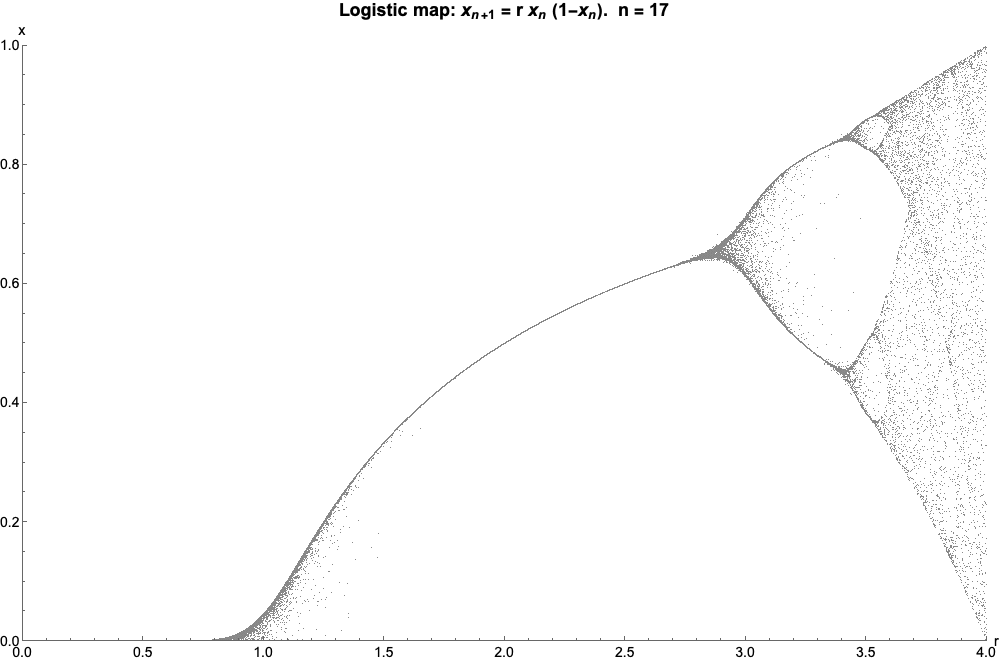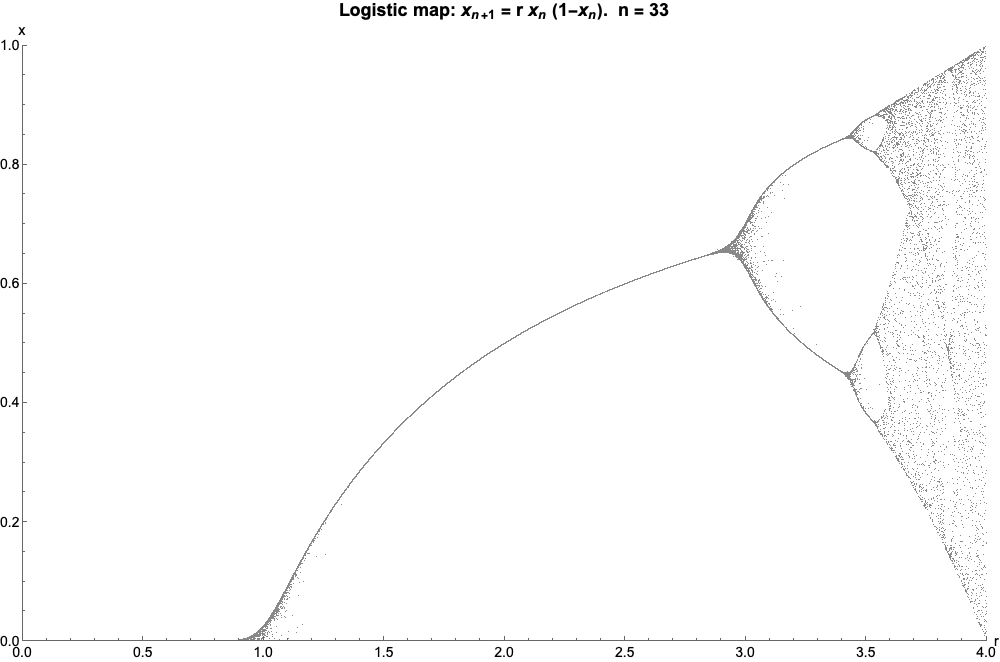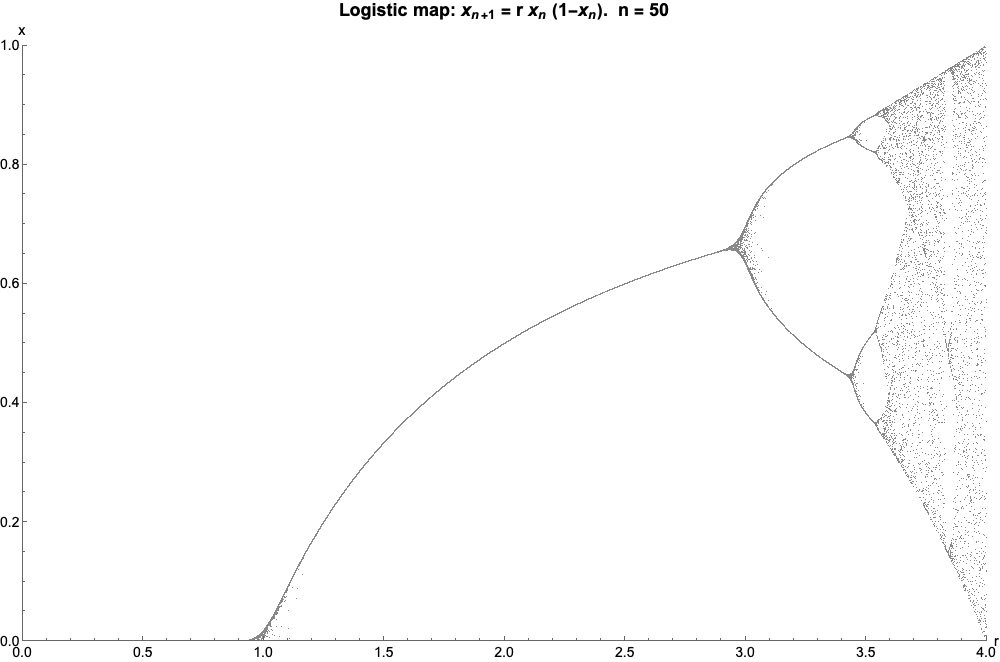
如果我们让n射向无穷大，看起来像这样（称为逻辑映射的分岔图）：

和那朋友们，就是曼德布洛集。

不，说真的。你看，曼德布洛特集也受递归关系的支配——即通过对当前数字进行某种操作来给出序列中的下一个数字的规则。对于逻辑映射，请记住，递归关系是

但对于曼德布洛特集来说，

现在，事情变得有点技术性了。这听起来可能很明显，但我们还是要说：逻辑斯蒂映射是一个映射，而曼德布洛特集是一个集合。我们知道这令人难以置信。但这种差异至关重要，因为这意味着它们告诉我们两个非常不同——几乎完全相反——的信息。虽然逻辑斯蒂映射会要求您提供一些起始值并返回振荡（如果您幸运的话），但曼德布洛特集却说“我们只想要来自这个递归关系的振荡——哪些起始值会给我们它们？”

让我们再看一个例子，以帮助我们理解：让我们是₀= 0 且C= 1. 然后我们发现

序列变得越来越大，没有界限，所以C= 1 不属于曼德布洛特集。另一方面，如果我们离开是₀= 0 并设置C= -1，我们得到

这些值在 0 和 -1 之间波动，因此C= -1 是曼德布洛特集合的一部分。明白了吗？

好吧，我们不会详细阐述，但请相信我们的话：如果你在图表上画出所有的复数C根据递归关系给出有界序列，可以得到：

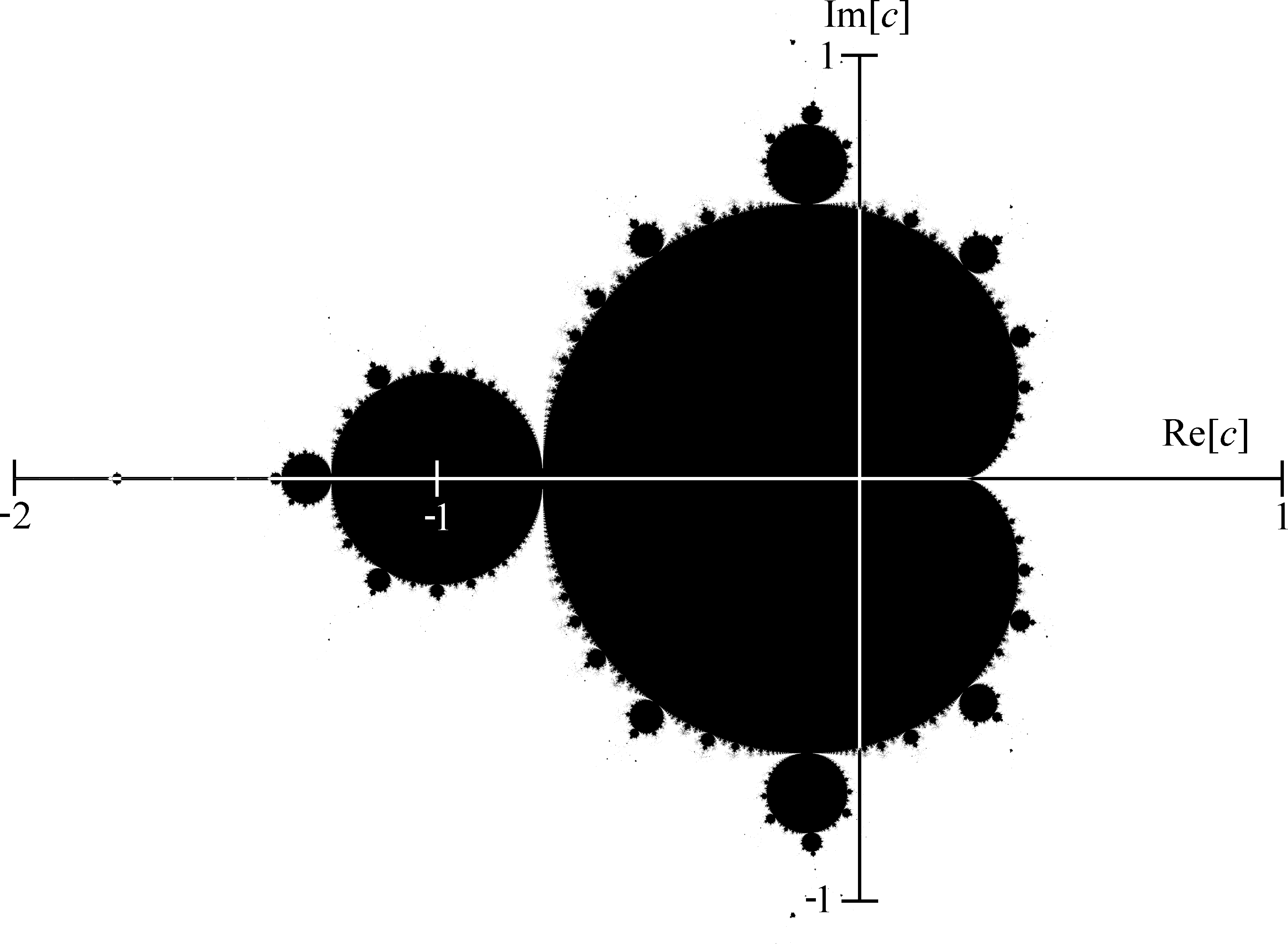
但如果我们想要更多信息呢？如果我们不仅想知道哪些值会波动，还想知道如何它们振荡吗？

好吧，这就是奇迹发生的地方。你也许已经注意到，我们之前将曼德布洛特集描述为一组复杂的数字。如果你不知道它们是什么，别担心——它们基本上只是一种扩展数字线以包含可以平方为负数的值的方法。但它们的主要特征是它们是二维的——不是数字线上的一个点，而是图形中的某个位置。

但这意味着，应用于复数的函数或递归关系无法给出像我们之前看到的分叉图那样的二维图形——水平“轴”实际上是一个平面。相反，我们必须将图表翻转过来，当我们这样做时，我们会看到一些东西字面上地惊人的。

物流地图！这可不是什么图形上的骗局——你可以用冷酷的数学从一个地图到另一个地图如果你真的想。引人注目的是，逻辑斯蒂映射的分裂点与曼德布洛特集和实数线的交点相对应——你甚至可以看到曼德布洛特集的“针”所代表的逻辑混沌区域。

但曼德布洛特集合不是仅有的逻辑斯蒂映射——那只是沿着实轴的部分。因此，虽然主心形线——曼德布洛分形中最大的心形部分——对应于逻辑斯蒂映射的独特部分，而主球状部分——分形的第二大部分——对应于映射中在两个值之间振荡的部分，依此类推，直到 4、8、16 等等，但曼德布洛集也有一些部分在逻辑斯蒂映射中根本没有表示出来。像位于主心形线顶部的最大球状部分这样的部分——此部分中的值振荡三次。在其左侧稍远处是一个球状部分，其值振荡五次。事实上，您可以选择任何您喜欢的正整数，并且在曼德布洛集的某个地方，您可以找到振荡次数恰好是这个数的值。

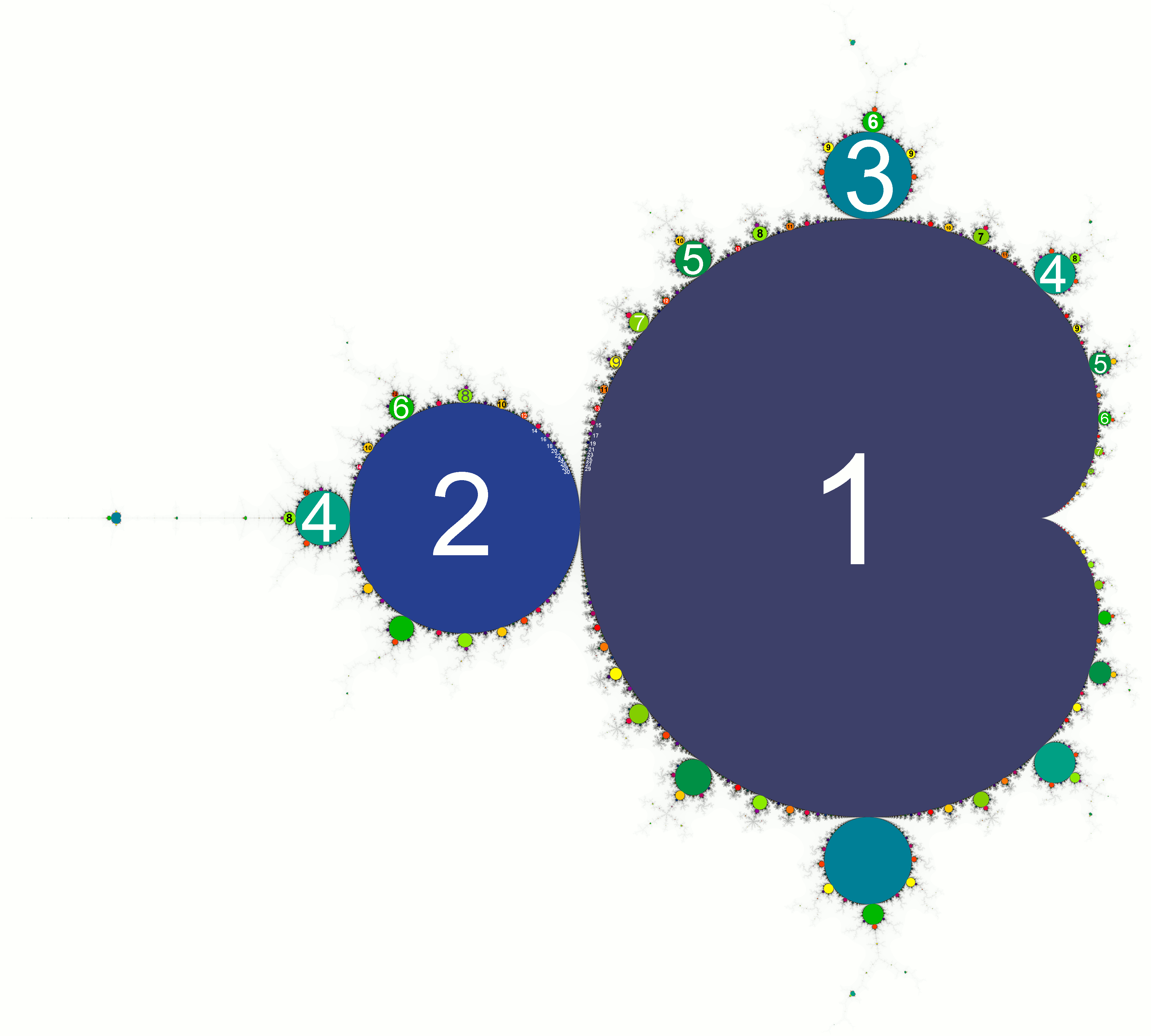
曼德布洛特集合具有许多令人惊叹的特性，其中许多可以在这部史诗般的 Veritasium 视频，但它与逻辑斯蒂映射的联系可以说是最令人着迷的联系之一——只是因为它囊括了数学的许多神奇之处。

让我们面对现实：在其他哪个科学领域，你可以让一群好色的兔子想出像曼德布洛特集合这样抽象而美丽的东西？