
本文最初發表在對話。該出版物將文章貢獻給Livessience的專家聲音:專家和見解。
數學最神奇的方面之一是使復雜和復雜的結構從最簡單的規則中出現的能力。很少有數學對象可以更簡單地創建,而且很少有像Pascal的奇妙三角形這樣的複雜模式。
自己做帕斯卡的三角形,您需要的只是筆和紙和一個非常簡單的規則 - 三角形中的每個數字是直接上方的兩個數字的總和。將數字像牆中的磚頭一樣,將1s放在每行的外部,然後添加 - 這樣:

Blaise Pascal是17世紀的法國數學家。他主要有興趣使用三角形來推進概率理論的研究 - 他或多或少地發明了這一領域費馬特石,在一位賭博朋友向帕斯卡(Pascal)詢問有關兩個骰子玩家應如何分配比賽的建議,如果他們的比賽很早就被中斷。
儘管製作簡單,但三角形掩蓋了許多令人驚訝的模式。所以,向民間頌歌一般而言弗雷德里克·奧斯丁尤其…
在聖誕節的第一天,三角形給了我…
計數數字(對稱)

從三角形中滾出的兩個最直接的模式是雙邊對稱性- 樹的左右兩半完美地鏡面 - 熟悉的景象計數數字沿著兩側的內部對角線行進。
在聖誕節的第二天,三角送給我…
兩個權力

添加每一行上的所有數字將揭示兩個的功能(並顯示2到0的功率真的想要等於1)。
在聖誕節的第三天,三角形給了我…
三角數

我們已經看到了第一個內部對角線的計數數字 - 現在讓我們將注意力轉向第二個對角線。假設您今年為朋友和家人烘烤聖誕節禮物,而您的想法有三角形。您需要烘烤幾種零食,以便以後可以以三角形的方式排列它們?
從技術上講,一種享受會做,但這就是數學家所說的小三角形(您的朋友可能會使用更豐富多彩的術語)。三個會更好。
您可以通過在原來的小三角形下再添加三個(總共六個)來增加三角形,或者通過再添加四個(總共十個)。
達到創建三角形的最佳位置的數字是適當命名的三角數,它們在兩側的第二個內側對角線下出現。
在聖誕節的第四天,三角送給我…
斐波那契

序列斐波那契的數字從1和1開始,然後每個後續的數字是直接出現的兩個數字的總和。他們是在1202年首次描述的斐波那契(或PISA的倫納多),在可以迅速執行乘法的兔子的背景下。
在帕斯卡爾的三角形中發現它們很棘手,但是它們可以躲藏起來!您可以發現它們散佈在三角形的“短對角線”上 - 在這些短對角線中加上數字將使您可以將斐波那契的數字拼湊在一起。
在聖誕節的第五天,三角送給我…
Prime…數量的東西!
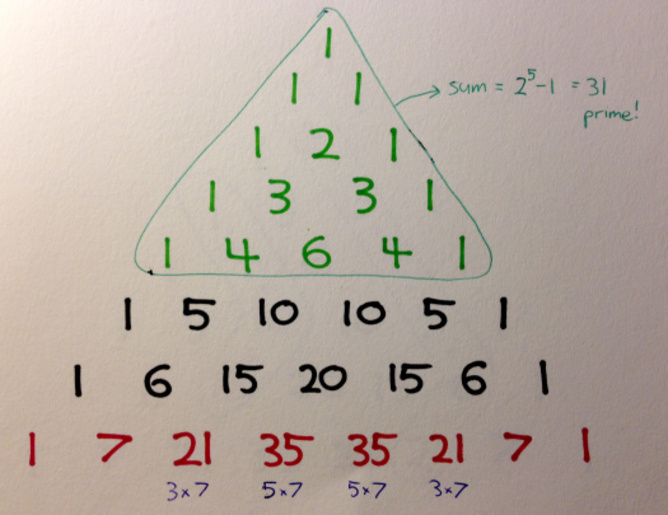
如果將第一個n行中的每個數字加起來,您將獲得nth梅森(Mersenne)號碼(這是n的功率2的數字僅1的數字)。 Mersenne的數字在數學研究的最前沿使用,以查找非常龐大的質量數,因為它們具有非常有趣的功能:如果n是質量數字,那麼不時的nth Mersenne數字也將是素數。
例如,在帕斯卡(Pascal)三角形的前5行中加起來所有數字使我們獲得了第五個梅森(Mersenne)的數字,即31(比5的功率小於2)。由於5是一個素數,因此31也可能是一個素數……而且碰巧是這樣。迄今為止,最大的已知梅森·普里姆(Mersenne Prime)IS(2至20996011的功率)減去1 - 一個具有6320430數字的數字!
帕斯卡爾的另一個主要模式是以下 - 如果您查看第一個內對角線上的計數數為素數(例如7),則每個行其他三角形的那一行中的數字將是該素數的倍數。除了外面的1秒。
在聖誕節的第六天,三角送給我…
交織的花瓣

選擇帕斯卡(Pascal)三角形內的任何數字,然後查看周圍的六個數字(在上面繪製的花朵中形成了交替的花瓣)。如果您將數字乘以每個第二花瓣中的數字,那麼無論您從哪個花瓣開始,最終都會得到相同的答案。
在聖誕節的第七天,三角送給我…
曲棍球加成
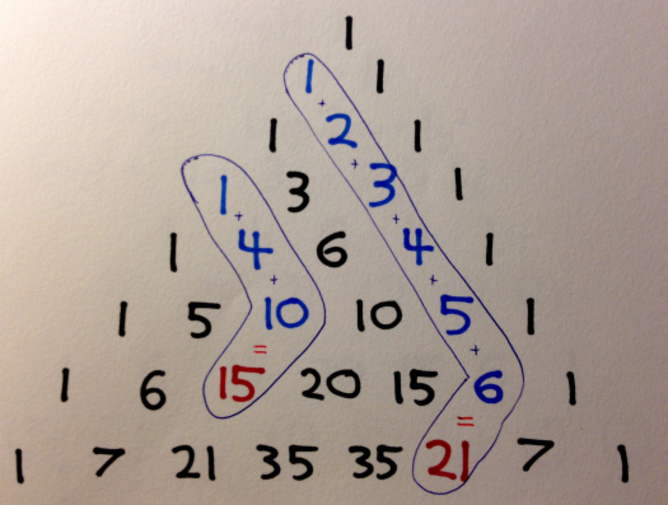
從最外側邊緣上的任何1秒開始,將任意數量的數字添加在一起,其中一個對角線之一。無論您在哪裡停下來,都會發現自己的總和在等待一個對角線的步驟 - 朝與前進的方向相反(因此“曲棍球”模式)。
在聖誕節的第八天,三角送給我…
通過添加

從第一個對角線和正方形中選擇任何計數號。然後查看其在三角形內部更深層次的兩個鄰居 - 它們始終將其累加到相同的平方數字中。
在聖誕節的第九天,三角送給我…
二項式係數
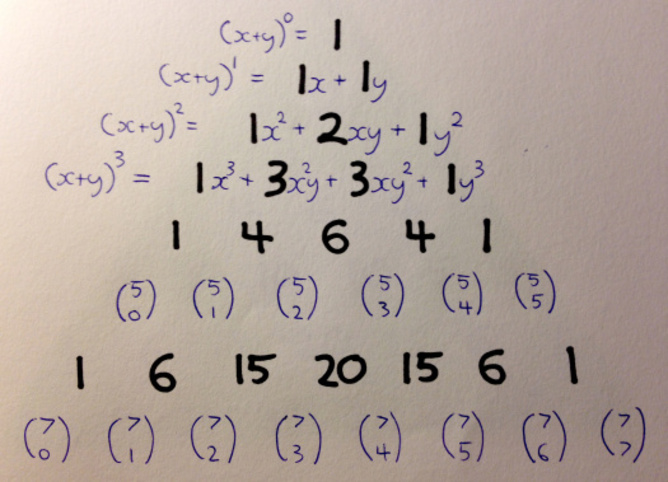
帕斯卡(Pascal)的三角形甚至可以使一些可怕的高中代數容易得多。
如果您發現自己處於不得不擴展到N的力量的不幸位置,則可以直接跳過所有可怕的鍛煉到答案。
首先,將X的所有N乘在一起,然後從左移到右移動時,將一個X卸下,然後用AY替換為AY,直到根本沒有X為止。
一旦將所有這些術語加起來,剩下要做的就是填充正確的係數。這將是練習中最困難的部分……如果不是因為您可以直接從Pascal的三角形上讀取它們!只需轉到第一個內部對角線上n的線,他們就會等待您。
這個魔術捷徑的秘訣是二項式定理為了擴展括號 - 加上帕斯卡三角形中的數字確實是偽裝的組合……
在聖誕節的第十天,三角形給了我…
所有組合
讓我們簡要回到帕斯卡爾三角的歷史根源。如上所述,帕斯卡爾三角形中的所有數字實際上對應於組合- 也就是說,他們準確地告訴我們,我們可以從一個較大的組中選擇一小群對象(如果我們選擇事物的順序並不重要的話)。
組合對於概率理論家及其賭博朋友非常重要,因為計算可能發生的事情的數量是確定其發生概率的最直接方法。
組合可以用多種方式編寫,但是最常見的符號是將兩個數字放入一對括號內 - 一個在頂部(告訴我們對象總數),一個在底部數字上(告訴我們我們要選擇多少個對象)。這些組合與Pascal的三角形完美匹配 - 最高數字與三角形的行匹配,底部數字告訴我們沿著行走了多遠。
例如,假設我們有5條水果和蔬菜:一個pple,abAnaana,cARROT,ad穀物和eggplant。我們想挑選其中2個用於我們的烹飪。我們可以做出多少可能的選擇?
我們可以仔細列出所有可能性(記住訂單沒關係) - 然後,我們將擁有AB,AC,AD,AE,BC,BD,BE,BE,CD,CE,CE,DE,以及總共10種可能性。另外,我們可以在帕斯卡(Pascal)的三角形中倒數5行(從0開始)和2個位置(再次從0開始) - 也達到數字10。
在聖誕節的第11天,三角形給了我…
十一的力量
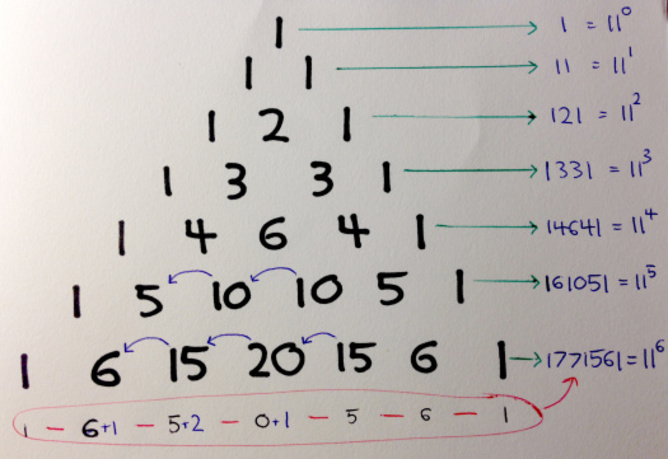
對於一個特別酷的派對技巧,請查看當您一起擠壓給定行中的所有數字以製作一個大數字時會發生什麼。實際上,在處理諸如兩位數的數字之類的時,我們必須要小心一點 - 而不是僅僅將它們擠在一起,而是將額外的數字移至左邊(與小學相似的方式)。
例如,當將1-4-6-4-1排擠在一起時,我們最終以數字14641。但是,當我們將1-5-10-10-5-1排擠壓在一起時,我們將10s分為1(將其添加到1(將添加到左上的數字)和0(保留下來)。
在以這種方式分配前10個時,行變為1-(5+1) - (0)-10-5-1。當第二個10分開時,該行最終以1-(5+1) - (0+1)-0-5-1或1-6-1-0-5-1,我們最終以數字161051(做到這一點要比描述它要容易得多,請相信我,請相信我!)。
就像連續添加數字可以將數字添加在一起,從而使我們具有兩個功能,將數字連續擠壓在一起,將它們像這樣擠在一起,從而使我們的力量達到了11個!另請注意,0的功率為11確實也希望等於1…
在聖誕節的第十二天,三角送給我…
Sierpinski的分形!

現在,我一直以來最喜歡的帕斯卡模式 - 我永遠不會對我的最愛感到驚訝分形有史以來三角形偷偷躲藏在帕斯卡爾的三角形中。
Siepinski的三角形是當您拿一個等邊三角形,切掉中間零件,然後將中間碎片從所有剩下的較小的三角形中切下中間碎片,然後永遠繼續前進(或直到您疲倦)時,是您所獲得的形狀。
這與Pascal的三角形有何關係?查看當您用一種顏色和所有偶數數字帶有不同顏色的所有奇數時,會發生什麼!
祝您聖誕快樂,新年快樂;願您的假期充滿有趣的數學和歡呼!因此,願您的頌歌因此被數學家無法觸及。
邁克爾·羅斯(Michael Rose)不適用於,諮詢,擁有股份或從任何公司或組織中受益的公司或收取資金,並且沒有相關的隸屬關係。









