在數學世界中,有兩件事始終成立:首先,一些最頑固和最複雜的問題往往在現實世界中有著令人驚訝的應用;其次,對於那些實際上花費所有時間的人來說在在現實世界中,這些問題似乎……嗯,。
本文的其餘部分位於付費牆後面。請登錄或訂閱以訪問完整內容。
以“沙發問題”為例:這個難題幾十年來一直困擾著數學家,而且幾乎所有搬過家的人都“解決”了這一難題。這是一個關於如何將弧形沙發移動到 90 度角的問題 - 是的,就像那一集一樣朋友們你們現在都在引用。
移動的數學
從技術上來說,沙發的問題是這個:在寬度為 1 的走廊中,可圍繞直角移動的最大面積區域是多少?最早被正式表述為1966年由奧地利裔加拿大數學家利奧·莫澤 (Leo Moser) 提出——儘管在此之前,這個問題多年來一直是圍繞數學飲水機的討論話題——但直到現在,還從未得到最終解決。
現在,您會注意到,此表述中沒有提及同名長椅,實際上,作為解決方案建議的第一件“家具”實際上是一架“鋼琴”。儘管如此,“沙發”這個術語很快就流行起來,主要是因為——好吧,看看它:
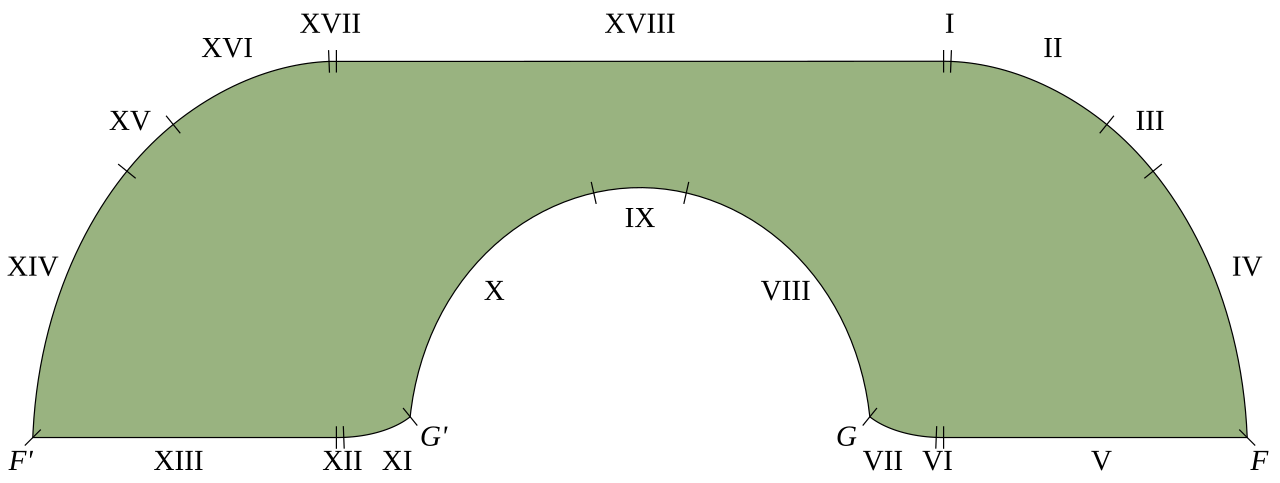
Gerver 沙發,顯示了構成其邊界的 18 個部分。
圖片來源:TilmannR via維基共享資源,公共領域。
正是對下限的確定催生了標誌性的沙發形狀:在 1968 年的一篇論文中,我們沒有騙你,論“現代數學”和學校和大學中類似的軟知識垃圾對數學技能的削弱約翰·哈默斯利 (John Hammersley) 通過一些相對簡單的微積分錶明,該形狀的面積為 (π/2) + (2/π) – 大約為 2.2074。
事實上,他走得更遠。在同一篇論文中,他證明了該面積的上限由 2√2 給出——大約為 2.8284。雖然只過了幾年,但沙發問題已經有了解決方案:確切的數字尚未確定,但數學家知道它必須在這兩個值之間。找到真正的答案肯定不需要做更多的工作嗎?
然而,25 年過去了,哈默斯利的彈跳仍然是我們最好的。直到羅格斯大學數學家 Joseph Gerver 站出來,提供了一張由 18 塊材料製成的沙發連接的曲線部分。眾所周知的“Gerver 沙發”將下限提高至 2.2195。
又過了四分之一個世紀,可能的解決方案的範圍才會進一步縮小:2018年,數學家 Yoav Kallus 和 Dan Romik 使用計算機輔助證明將上限降低至 2.37。
這對哈默斯利最初的界限來說是一個很大的改進——但這個精確的解決方案仍然無法被捕獲。
白克在比賽中
大約在卡勒斯和羅米克研究解決方案的同時,韓國首爾延世大學的博士後研究員 Jineon Baek 第一次開始思考沙發問題。現在,七年後,他認為他已經在尚未經過同行評審的證明中破解了這個問題。
“我為此投入了大量時間,但到目前為止還沒有發表任何文章,”他告訴新科學家。 “現在我可以向世界說,我為這個問題做出了一些有價值的貢獻,這一事實正在得到證實。”
對於一個如此容易陳述和想像的問題,白的證明並不是一件容易的事。它橫跨 100 多頁,它的作用遠遠不只是簡單地暴力解決問題或不斷地削減更小的區域。相反,羅米克告訴《新科學家》,這是一個“奇妙的發展”。
“我知道我永遠不可能做到這一點,”羅米克說。 “我沒有後悔的感覺,或者說,我怎麼能錯過這個,因為很明顯,這不是我認為我能夠做到的那種想法。[Baek] 只是從一個完全不同的方向來考慮。”
無需深入討論細節,證明是這樣的:首先,Baek 說,最佳沙發,無論結果是什麼,都必須具有三個特定屬性 - 它必須是單調的、平衡的,並且具有 π/2 的旋轉角度。同樣,這些定義是相當技術性的,但本質上可以歸結為:到目前為止我們使用的“沙發”已經幾乎是正確的形狀了。
其次,Baek 開始證明這張沙發如何移動到拐角處的條件——雖然是一件小事,但對於完成最後一步至關重要:定義這張沙發麵積的上限,然後證明它等於 Gerver 的下限。
沒錯:32 年後,事實證明 Gerver 一直都是對的。
“我當然對這一切感到非常高興,”格弗告訴《新科學家》。 “我已經75歲了,而白不可能超過30歲。他比我有更多的精力、耐力和存活的腦細胞,我很高興他接過了接力棒。我也很高興我活得足夠長,可以看到他完成我開始的事情。”
把腳抬起來
那麼,沙發問題現在解決了嗎?嗯,從技術上講,這還有待觀察。與所有數學證明一樣,它需要經過同行評審以確保准確性——Baek 對此暗暗抱有希望。
“我不能說我百分百有信心,因為我們是人類,我們會犯錯誤,”他告訴新科學家。 “但是,我還是盡了最大努力讓自己變得自信。”
但如果您自己解決沙發問題的希望因這個消息而破滅,請放心:既然 Baek 如此嚴格地定義了他的沙發,您隨時可以為自己選擇不同的形狀。
當然,它可能不太適合你的客廳沙發,但你可能會說,沒有什麼能阻止你去……白去畫板。
證據可以找到在 ArXiv 預印本服務器上。









