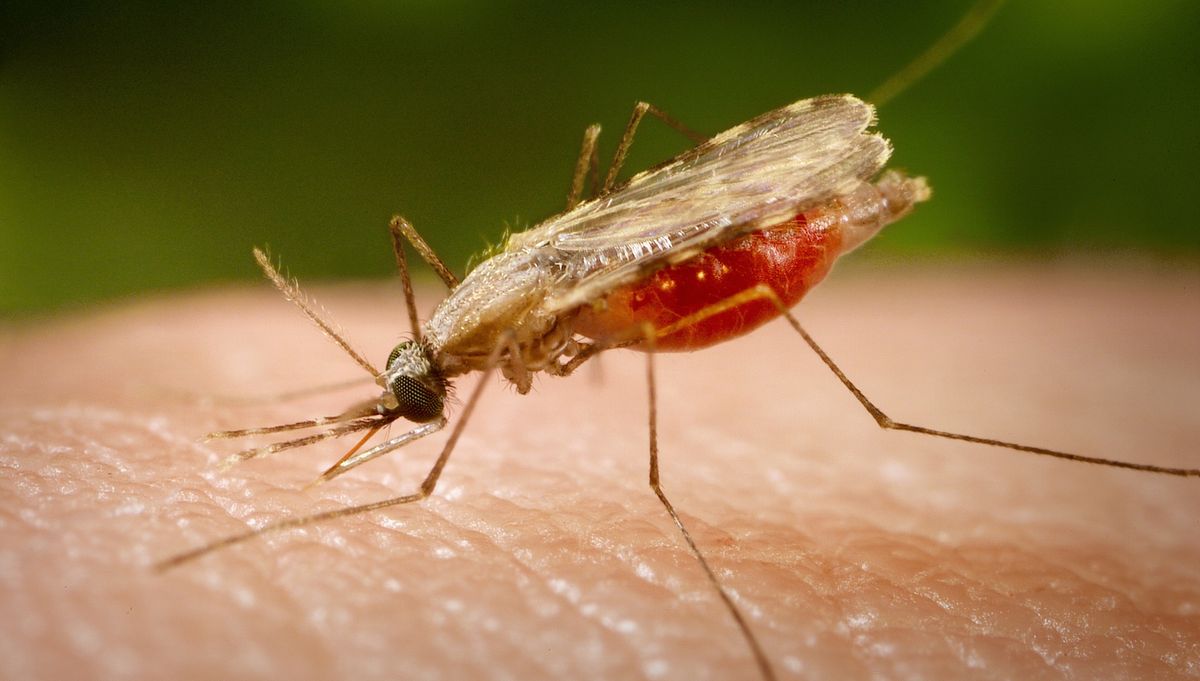
น่าเบื่อหรือไม่?

คณิตศาสตร์เป็นหนึ่งในพื้นที่แห่งความรู้เดียวที่สามารถอธิบายได้อย่างเป็นกลางว่า "จริง" เพราะทฤษฎีบทของมันได้มาจากตรรกะบริสุทธิ์ และในขณะเดียวกันทฤษฎีบทเหล่านั้นมักจะแปลกมากและตอบโต้ได้ง่าย
บางคนพบว่าคณิตศาสตร์น่าเบื่อ ดังตัวอย่างเหล่านี้แสดงให้เห็นว่ามันเป็นอะไรก็ได้ แต่
รูปแบบสุ่ม
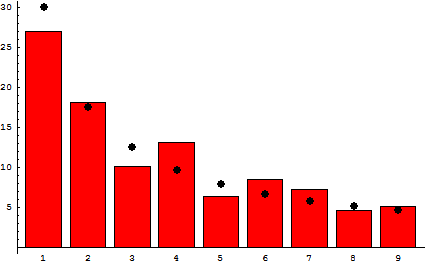
ข้อมูลสุ่มไม่ได้เป็นแบบสุ่มทั้งหมด ในรายการตัวเลขที่แสดงถึงอะไรก็ได้จากราคาหุ้นสำหรับประชากรในเมืองถึงความสูงของอาคารตามความยาวของแม่น้ำประมาณ 30 เปอร์เซ็นต์ของตัวเลขจะเริ่มต้นด้วยตัวเลข 1 น้อยกว่าจะเริ่มต้นด้วย 2 แม้จะน้อยกว่า 3 และอื่น ๆ จนกระทั่งมีเพียงจำนวนหนึ่งในยี่สิบจะเริ่มต้นด้วย 9
หมุนวน
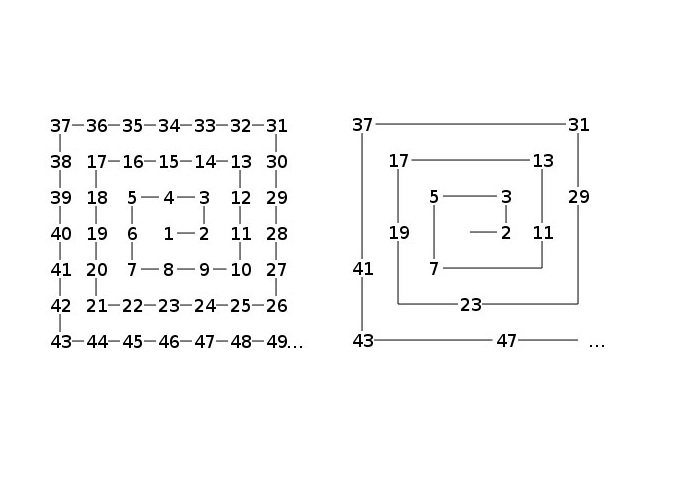
เนื่องจากตัวเลขที่สำคัญไม่สามารถแบ่งแยกได้ (ยกเว้น 1 และตัวเอง) และเนื่องจากตัวเลขอื่น ๆ ทั้งหมดสามารถเขียนเป็นทวีคูณของพวกเขาพวกเขาจึงมักถูกมองว่าเป็น "อะตอม" ของโลกคณิตศาสตร์ แม้จะมีความสำคัญ แต่การกระจายตัวของจำนวนที่สำคัญในจำนวนเต็มยังคงเป็นปริศนา ไม่มีรูปแบบที่กำหนดตัวเลขที่จะเป็นนายกหรือเป็นระยะเวลาที่ต่อเนื่องกัน
การสุ่มที่ดูเหมือนของช่วงเวลาทำให้รูปแบบที่พบใน "Ulam Spirals" แปลกมากจริงๆ
ในปี 1963 นักคณิตศาสตร์ Stanislaw Ulam สังเกตเห็นรูปแบบที่แปลกในขณะที่ Doodling ในสมุดบันทึกของเขาในระหว่างการนำเสนอ: เมื่อจำนวนเต็มถูกเขียนเป็นเกลียวตัวเลขสำคัญมักจะตกตามแนวทแยงมุม สิ่งนี้ในตัวมันเองไม่น่าแปลกใจเลยเพราะตัวเลขที่สำคัญทั้งหมดยกเว้นหมายเลข 2 นั้นแปลกและเส้นแนวทแยงมุมในเกลียวจำนวนเต็มนั้นแปลกและแม้กระทั่ง ความตกใจมากขึ้นคือแนวโน้มของจำนวนนายกที่จะนอนต่อบางเส้นทแยงมุมมากกว่าคนอื่น ๆ - และสิ่งนี้เกิดขึ้นไม่ว่าคุณจะเริ่มต้นด้วย 1 ที่อยู่ตรงกลางหรือหมายเลขอื่น ๆ
แม้ว่าคุณจะซูมออกเป็นขนาดที่ใหญ่กว่าเช่นเดียวกับในพล็อตของตัวเลขหลายร้อยด้านล่างคุณสามารถเห็นเส้นทแยงมุมที่ชัดเจน (จุดสีดำ) โดยมีบางบรรทัดที่แข็งแกร่งกว่าคนอื่น ๆ มีการคาดเดาทางคณิตศาสตร์ว่าทำไมรูปแบบที่สำคัญนี้จึงเกิดขึ้น แต่ไม่มีการพิสูจน์แล้ว
Sphere Eversion

{youtube i6cgca4mmcc & feature = เกี่ยวข้อง}
ในสาขาคณิตศาสตร์ที่สำคัญที่เรียกว่าทอพอโลยีวัตถุสองชิ้นได้รับการพิจารณาว่าเทียบเท่าหรือ "homeomorphic" หากสามารถปรับเปลี่ยนไปได้โดยการบิดและยืดพื้นผิวของมัน พวกเขาจะแตกต่างกันถ้าคุณต้องตัดหรือยุบพื้นผิวของหนึ่งเพื่อปรับเปลี่ยนเป็นรูปแบบของอีกรูปแบบหนึ่ง
ลองพิจารณาตัวอย่างเช่น torus-วัตถุรูปดั๊กนัทที่แสดงในสไลด์อินโทร หากคุณหมุนตัวตรงให้กว้างขึ้นด้านหนึ่งและเยื้องด้านบนของด้านนั้นคุณจะมีวัตถุทรงกระบอกที่มีที่จับ ดังนั้นเรื่องตลกทางคณิตศาสตร์แบบคลาสสิกคือการบอกว่านักโทโพโลยีไม่สามารถบอกโดนัทจากถ้วยกาแฟของพวกเขาได้
ในทางกลับกันแถบ Moebius-ลูปที่มีการบิดตัวเดียว-ไม่ใช่ homeomorphic ที่มีลูปที่ไม่มีการบิด (กระบอกสูบ) เพราะคุณไม่สามารถบิดออกจากแถบ Moebius ได้โดยไม่ต้องตัดออก
นักโทโพโลยิคนสงสัยมานาน: เป็นทรงกลม homeomorphic ที่มีรุ่นภายในของตัวเองหรือไม่? กล่าวอีกนัยหนึ่งคุณสามารถเปลี่ยนทรงกลมภายในออกได้หรือไม่? ในตอนแรกดูเหมือนว่าเป็นไปไม่ได้เพราะคุณไม่ได้รับอนุญาตให้โผล่รูในทรงกลมและดึงด้านในออกมา แต่ในความเป็นจริง "Sphere Eversion" ตามที่เรียกว่าเป็นเป็นไปได้. ดูวิดีโอด้านบนเพื่อดูว่ามันทำอย่างไร
อย่างไม่น่าเชื่อนักโทวิทยา Bernard Morin ผู้พัฒนาหลักของวิธีการที่ซับซ้อนของ Sphere Eversion ที่แสดงที่นี่เป็นคนตาบอด
คณิตศาสตร์ผนัง

แม้ว่าพวกเขาอาจจะได้รับการตกแต่งด้วยความเจริญรุ่งเรืองที่ไม่มีที่สิ้นสุดการพูดทางคณิตศาสตร์ แต่ก็มีรูปแบบเรขาคณิตที่แตกต่างกันจำนวน จำกัด ภาพวาด Escher ทั้งหมดวอลล์เปเปอร์การออกแบบกระเบื้องและการเตรียมการทำซ้ำสองมิติทั้งหมดสามารถระบุได้ว่าเป็นของหนึ่งหรืออื่น ๆ ที่เรียกว่า "กลุ่มวอลล์เปเปอร์" และมีกลุ่มวอลล์เปเปอร์กี่กลุ่ม? 17. [เครื่องคิดเลขคำนวณอย่างไร?-
โคลง
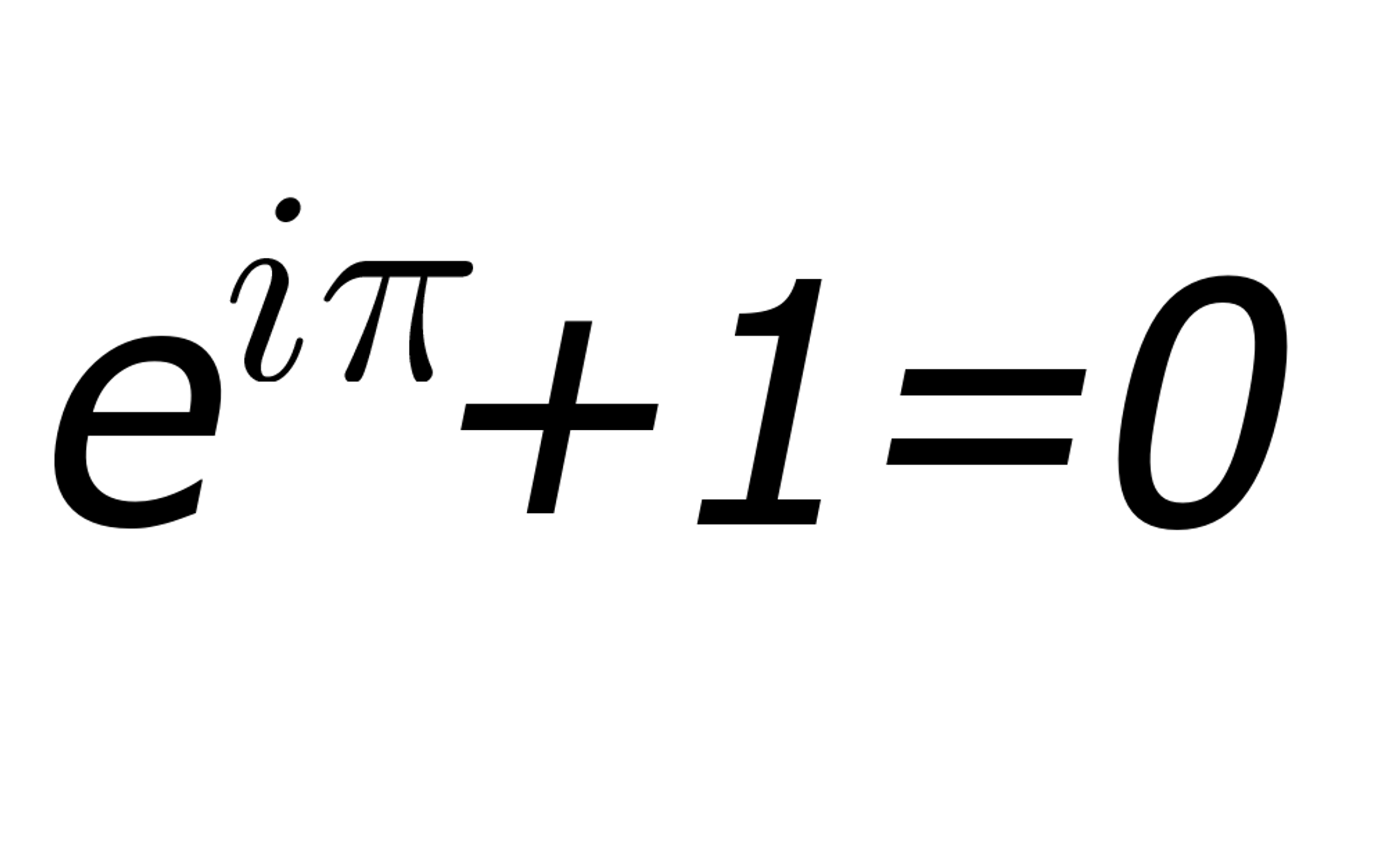
"เหมือนโคลนของเชคสเปียร์ที่รวบรวมสาระสำคัญของความรักหรือภาพวาดที่นำความงามของรูปแบบมนุษย์ที่เป็นมากกว่าแค่ผิวลึกสมการออยเลอร์ก็เข้าสู่ระดับลึกของการดำรงอยู่"
นักคณิตศาสตร์ Stanford Keith Devlin เขียนคำเหล่านี้เกี่ยวกับสมการทางซ้ายในเรียงความปี 2002 ที่เรียกว่า "สมการที่สวยที่สุด" แต่ทำไมสูตรของออยเลอร์ถึงน่าทึ่ง? แล้วหมายความว่าอย่างไร?
ขั้นแรกจดหมาย "E" แสดงถึงจำนวนที่ไม่มีเหตุผล (ที่ไม่มีตัวเลขไม่สิ้นสุด) ที่เริ่มต้น 2.71828 ... ค้นพบในบริบทของความสนใจอย่างต่อเนื่องมันควบคุมอัตราการเติบโตแบบเอ็กซ์โปเนนเชียลจากประชากรแมลงไปจนถึงการสะสมความสนใจ ในวิชาคณิตศาสตร์จำนวนแสดงคุณสมบัติที่น่าแปลกใจบางอย่างเช่น - เพื่อใช้คำศัพท์ทางคณิตศาสตร์ - เท่ากับผลรวมของการผกผันของแฟคทอเรียลทั้งหมดตั้งแต่ 0 ถึงอินฟินิตี้ อันที่จริงแล้วคณิตศาสตร์ "E" คงที่ที่ดูเหมือนจะปรากฏขึ้นจากที่ใดในสมการที่สำคัญจำนวนมาก
ถัดไป "ฉัน" หมายถึงสิ่งที่เรียกว่า "จำนวนจินตภาพ": สแควร์รูทของลบ 1 มันถูกเรียกเพราะในความเป็นจริงไม่มีจำนวนที่สามารถคูณด้วยตัวเองเพื่อสร้างจำนวนลบ (และจำนวนลบจึงไม่มีรากสี่เหลี่ยมจริง) แต่ในวิชาคณิตศาสตร์มีหลายสถานการณ์ที่หนึ่งถูกบังคับให้ใช้รากที่สองของลบ ตัวอักษร "ฉัน" จึงถูกใช้เป็นแบบยืนเพื่อทำเครื่องหมายสถานที่ที่ทำสิ่งนี้
PI อัตราส่วนของเส้นรอบวงของวงกลมต่อเส้นผ่านศูนย์กลางของมันเป็นหนึ่งในตัวเลขที่รักและน่าสนใจที่สุดในคณิตศาสตร์ เช่นเดียวกับ "E" ดูเหมือนว่าจะเกิดขึ้นในสูตรคณิตศาสตร์และฟิสิกส์จำนวนมากอะไรทำให้ Pi พิเศษมาก?-
รวมทุกอย่างเข้าด้วยกัน "E" คงที่ยกขึ้นสู่พลังของจินตนาการ "i" คูณด้วย pi เท่ากับ -1 และดังที่เห็นในสมการของออยเลอร์เพิ่ม 1 ถึงสิ่งที่ให้ 0 ดูเหมือนว่าแทบไม่น่าเชื่อเลยว่าตัวเลขแปลก ๆ เหล่านี้ทั้งหมด - และแม้แต่สิ่งที่ไม่จริง - จะรวมเข้าด้วยกัน แต่มันคือพิสูจน์แล้วข้อเท็จจริง.