บทความนี้เผยแพร่ครั้งแรกที่บทสนทนา-สิ่งพิมพ์มีส่วนร่วมในบทความของ LiveScience'sVoices Expert: Op-Ed & Insights-
หนึ่งในแง่มุมที่น่าอัศจรรย์ที่สุดของคณิตศาสตร์คือความสามารถสำหรับโครงสร้างที่ซับซ้อนและซับซ้อนที่จะเกิดขึ้นจากกฎที่ง่ายที่สุด วัตถุทางคณิตศาสตร์เพียงไม่กี่ชิ้นนั้นง่ายกว่าในการสร้าง - และไม่กี่สานความหลากหลายของรูปแบบที่สลับซับซ้อน - เป็นสามเหลี่ยมที่ยิ่งใหญ่ของ Pascal
เพื่อสร้างของคุณเองรูปสามเหลี่ยมของปาสกาลทั้งหมดที่คุณต้องการคือปากกาและกระดาษและกฎง่ายๆหนึ่งข้อ - แต่ละหมายเลขในสามเหลี่ยมคือผลรวมของตัวเลขสองตัวด้านบนโดยตรง จัดเรียงตัวเลขขึ้นเช่นอิฐในผนังวาง 1 วินาทีลงด้านนอกของแต่ละแถวและเพิ่ม - เช่น:

Blaise Pascalเป็นนักคณิตศาสตร์ชาวฝรั่งเศสในศตวรรษที่ 17 เขามีความสนใจเป็นหลักในการใช้รูปสามเหลี่ยมเพื่อพัฒนาทฤษฎีความน่าจะเป็น - สนามที่เขาคิดค้นขึ้นมามากหรือน้อยในการติดต่อกับหินเฟอร์มัตหลังจากเพื่อนนักพนันถาม Pascal เพื่อขอคำแนะนำเกี่ยวกับวิธีที่ผู้เล่นลูกเต๋าสองคนควรแบ่งหม้อหากเกมของพวกเขาถูกขัดจังหวะ แต่เนิ่นๆ
แม้ว่าจะง่ายที่จะทำรูปสามเหลี่ยมก็ซ่อนรูปแบบที่น่าประหลาดใจมากมาย ดังนั้นด้วยการขอโทษCarols พื้นบ้านโดยทั่วไปและเฟรเดอริกออสตินโดยเฉพาะอย่างยิ่ง ...
ในวันแรกของคริสต์มาสสามเหลี่ยมให้ฉัน ...
จำนวนการนับ (ด้วยสมมาตร)

สองรูปแบบทันทีที่สุดที่หลุดออกจากรูปสามเหลี่ยมคือมันสมมาตรทวิภาคี- ครึ่งด้านซ้ายและขวาของต้นไม้สะท้อนกันและกันอย่างสมบูรณ์ - และสายตาของคนที่คุ้นเคยการนับตัวเลขเดินไปตามเส้นทแยงมุมภายในในแต่ละด้าน
ในวันที่สองของคริสต์มาสสามเหลี่ยมให้ฉัน ...
พลังของสอง

การเพิ่มตัวเลขทั้งหมดในแต่ละแถวจะเปิดเผยพลังทั้งหมดของสอง (และแสดงให้เห็นว่า 2 ถึงพลังของ 0จริงหรือต้องการที่จะเท่ากับ 1)
ในวันที่สามของคริสต์มาสสามเหลี่ยมให้ฉัน ...
ตัวเลขสามเหลี่ยม

เราได้เห็นตัวเลขการนับตามเส้นทแยงมุมภายในครั้งแรก - ตอนนี้เรามาหันความสนใจของเราไปที่เส้นทแยงมุมที่สอง สมมติว่าคุณกำลังอบสินค้าคริสต์มาสสำหรับเพื่อนและครอบครัวในปีนี้และคุณมีสามเหลี่ยมในใจของคุณ คุณจะต้องอบกี่ขนมเพื่อที่คุณจะได้จัดเรียงในรูปแบบสามเหลี่ยมในภายหลัง?
ในทางเทคนิคหนึ่งการรักษาจะทำ แต่นั่นคือสิ่งที่นักคณิตศาสตร์เรียกว่าสามเหลี่ยมเล็ก ๆ น้อย ๆ (เพื่อนของคุณอาจใช้คำที่มีสีสันมากขึ้น) สามจะดีกว่า
คุณสามารถเติบโตสามเหลี่ยมของขวัญของคุณโดยเพิ่มอีกสาม (รวมทั้งหมดหก) ใต้สามเหลี่ยมขนาดเล็กดั้งเดิมของคุณ - หรือยังคงเพิ่มเติมโดยเพิ่มอีกสี่ (รวมทั้งหมดสิบ)
ตัวเลขที่มีจุดหวานสำหรับการสร้างรูปสามเหลี่ยมนั้นมีชื่ออย่างเหมาะสมตัวเลขสามเหลี่ยมและพวกเขาปรากฏตัวในเส้นทแยงมุมภายในที่สองในแต่ละด้าน
ในวันที่สี่ของคริสต์มาสสามเหลี่ยมให้ฉัน ...
ฟีโบนักชี

ลำดับของตัวเลขของ Fibonacciเริ่มต้นด้วย 1 และ 1 จากนั้นแต่ละหมายเลขที่ตามมาคือผลรวมของตัวเลขสองตัวที่เกิดขึ้นก่อนหน้านี้ พวกเขาได้รับการอธิบายครั้งแรกในปี 1202 โดยฟีโบนักชี(หรือ Leonardo of Pisa) ในบริบทของกระต่ายที่สามารถทำการคูณได้อย่างรวดเร็ว
พวกเขาเป็นเรื่องยากที่จะมองเห็นสามเหลี่ยมของ Pascal แต่พวกเขาสามารถเกลี้ยกล่อมจากการซ่อนตัว! คุณสามารถพบว่าพวกเขากระจัดกระจายไปทั่ว“ เส้นทแยงมุมสั้น” ของสามเหลี่ยม - การเพิ่มตัวเลขในเส้นทแยงมุมสั้น ๆ เหล่านี้จะช่วยให้คุณสามารถแยกตัวเลขของ Fibonacci เข้าด้วยกัน
ในวันที่ห้าของคริสต์มาสสามเหลี่ยมให้ฉัน ...
Prime … Num-Ber Things!
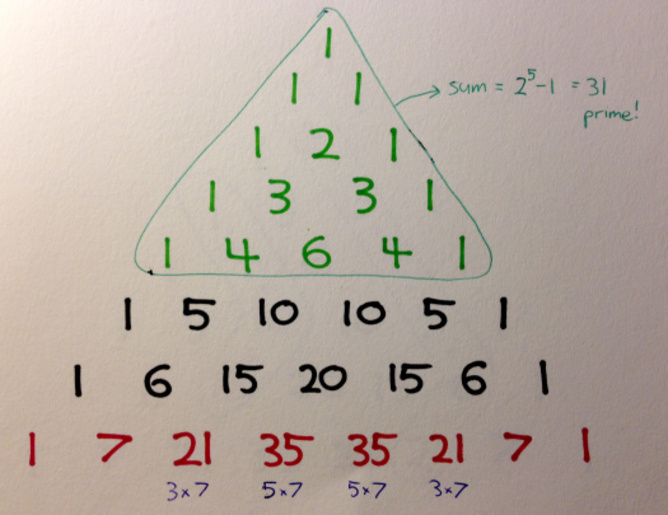
หากคุณเพิ่มทุกหมายเลขในแถวแรก N คุณจะได้รับ nthหมายเลข Mersenne(ซึ่งเป็นจำนวนที่ลดลง 1 สั้นของการเป็น 2 ถึงพลังของ n) ตัวเลข Mersenne ถูกนำมาใช้ที่การวิจัยทางคณิตศาสตร์ที่ทันสมัยเพื่อค้นหาตัวเลขที่สำคัญมากเพราะพวกเขามีคุณสมบัติที่น่าสนใจมาก: ถ้า n เป็นจำนวนที่สำคัญจากนั้นทุกครั้งที่หมายเลข Nth Mersenne ก็เป็นเรื่องสำคัญเช่นกัน
ตัวอย่างเช่นการเพิ่มตัวเลขทั้งหมดใน 5 แถวแรกของสามเหลี่ยม Pascal ให้หมายเลข Mersenne ที่ 5 ของเรา, 31 (ซึ่งน้อยกว่า 2 ถึง 2 ถึงพลัง 5) เนื่องจาก 5 เป็นจำนวนที่สำคัญมีความเป็นไปได้ที่ 31 อาจเป็นตัวเลขที่สำคัญเช่นกัน…และมันก็เกิดขึ้นเช่นนั้น จนถึงปัจจุบันที่รู้จักมากที่สุดMersenne Primeคือ (2 ถึงพลังของ 20996011) ลบ 1 - ตัวเลขที่มีตัวเลข 6320430!
รูปแบบสำคัญของ Pascal อีกอย่างหนึ่งคือสิ่งต่อไปนี้ - ถ้าคุณดูแถวที่จำนวนการนับในเส้นทแยงมุมชั้นในแรกคือ Prime (เช่น 7)อื่นจำนวนในแถวนั้นของสามเหลี่ยมจะเป็นจำนวนที่สำคัญ ยกเว้น 1s ด้านนอกนั่นคือ
ในวันที่หกของคริสต์มาสสามเหลี่ยมให้ฉัน ...
กลีบดอก

เลือกหมายเลขใด ๆ ภายในรูปสามเหลี่ยมของ Pascal และดูตัวเลขหกตัวที่อยู่รอบ ๆ หากคุณคูณตัวเลขในกลีบดอกที่สองทุกครั้งคุณจะจบลงด้วยคำตอบเดียวกันไม่ว่าคุณจะเริ่มกลีบใด
ในวันคริสต์มาสที่เจ็ดสามเหลี่ยมมอบให้ฉัน ...
การเพิ่มฮอกกี้ติด
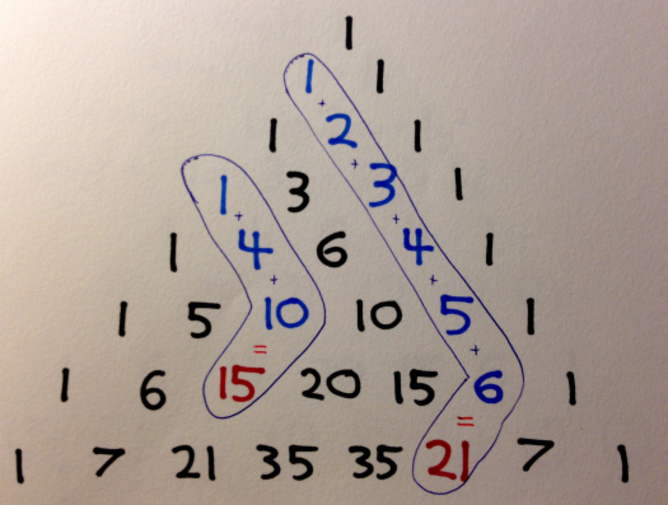
เริ่มต้นจาก 1s ใด ๆ ที่ขอบด้านนอกสุดรวมกันมากเท่าที่คุณชอบลงหนึ่งในเส้นทแยงมุม ไม่ว่าคุณจะหยุดที่ไหนคุณจะพบว่าผลรวมของคุณกำลังรอเพียงหนึ่งขั้นตอนในแนวทแยง-ในทิศทางตรงกันข้ามกับที่คุณกำลังมุ่งหน้า (ด้วยรูปแบบ "ฮอกกี้ติด")
ในวันคริสต์มาสที่แปดสามเหลี่ยมมอบให้ฉัน ...
กำลังเผชิญหน้ากับการเพิ่ม

เลือกหมายเลขการนับใด ๆ จากตามแนวทแยงครั้งแรกและสี่เหลี่ยมจัตุรัส จากนั้นดูเพื่อนบ้านสองคนที่อยู่ลึกเข้าไปในรูปสามเหลี่ยม - พวกเขาจะรวมกันเป็นสี่เหลี่ยมจัตุรัสเดียวกันเสมอ
ในวันที่เก้าของคริสต์มาสสามเหลี่ยมมอบให้ฉัน ...
ค่าสัมประสิทธิ์ทวินาม
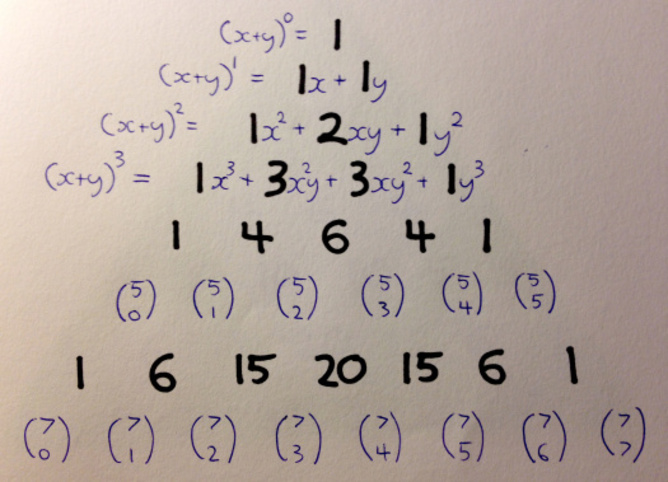
สามเหลี่ยมของ Pascal สามารถทำให้พีชคณิตโรงเรียนมัธยมที่น่ากลัวได้ง่ายขึ้นมาก
หากคุณพบว่าตัวเองอยู่ในตำแหน่งที่โชคร้ายที่ต้องขยาย (x+y) ไปยังพลังของ N คุณสามารถข้ามผ่านสิ่งที่น่ากลัวทั้งหมดที่ทำงานออกไปเพื่อตอบ
เริ่มต้นด้วยการวาง N ทั้งหมดของ X คูณด้วยกันและเมื่อคุณย้ายจากซ้ายไปขวาลบหนึ่ง X และแทนที่ด้วย AY จนกว่าจะไม่มี X เหลืออยู่เลย
เมื่อคุณเพิ่มข้อกำหนดทั้งหมดเหล่านี้สิ่งที่เหลือให้ทำคือกรอกค่าสัมประสิทธิ์ที่ถูกต้อง นี่จะเป็นส่วนที่ยากที่สุดของการออกกำลังกาย…หากไม่ใช่เพราะคุณสามารถอ่านได้ตรงสามเหลี่ยมของ Pascal! เพียงไปที่บรรทัดที่มี n ในเส้นทแยงมุมแรกภายในและพวกเขาจะรอคุณอยู่
ความลับของทางลัดเวทมนตร์นี้คือทฤษฎีบททวินามสำหรับการขยายวงเล็บ - พร้อมกับความจริงที่ว่าตัวเลขในสามเหลี่ยมของ Pascal นั้นเป็นการรวมกันในการปลอมตัว ...
ในวันที่สิบของคริสต์มาสสามเหลี่ยมให้ฉัน ...
ชุดค่าผสมทั้งหมด
ลองกลับไปสู่รากเหง้าทางประวัติศาสตร์ของสามเหลี่ยม Pascal สั้น ๆ ดังที่ได้กล่าวไว้ข้างต้นตัวเลขทั้งหมดในสามเหลี่ยมของ Pascal นั้นสอดคล้องกับการรวมกัน- นั่นคือพวกเขาบอกเราว่าเราสามารถเลือกวัตถุกลุ่มเล็ก ๆ ได้กี่วิธีจากกลุ่มที่ใหญ่กว่า (ถ้าลำดับที่เราเลือกสิ่งต่าง ๆ ไม่สำคัญ)
การรวมกันมีความสำคัญอย่างยิ่งต่อนักทฤษฎีความน่าจะเป็นและเพื่อนพนันของพวกเขาเนื่องจากการนับจำนวนวิธีที่บางสิ่งบางอย่างสามารถเกิดขึ้นได้เป็นวิธีที่ตรงไปตรงมาที่สุดในการกำหนดความน่าจะเป็นที่เกิดขึ้น
การรวมกันสามารถเขียนได้หลายวิธี แต่สัญกรณ์ที่พบบ่อยที่สุดคือการใส่ตัวเลขสองตัวไว้ในวงเล็บคู่หนึ่ง - หนึ่งด้านบน (เพื่อบอกจำนวนวัตถุทั้งหมด) และอีกหนึ่งหมายเลขด้านล่าง (เพื่อบอกเราว่าเราจะเลือกวัตถุจำนวนเท่าใด) และชุดค่าผสมเหล่านี้เข้ากันได้อย่างสมบูรณ์แบบกับรูปสามเหลี่ยมของ Pascal - หมายเลขด้านบนตรงกับแถวของสามเหลี่ยมและหมายเลขล่างบอกเราว่าไกลแค่ไหนตามแถวที่จะไป
ตัวอย่างเช่นบอกว่าเรามีผักและผลไม้ 5 ชิ้น: ANอันpple, aขAnaana, aCarrot, adข้าวและอีggplant เราต้องการเลือก 2 คนให้ใช้ในการทำอาหารของเรา เราสามารถเลือกได้กี่ทางเลือก?
เราสามารถแสดงความเป็นไปได้ทั้งหมดอย่างรอบคอบ (จำได้ว่าคำสั่งไม่สำคัญ) - จากนั้นเราจะมี AB, AC, AD, AE, BC, BD, BE, CD, CE, DE และความเป็นไปได้ทั้งหมด 10 ประการ อีกทางเลือกหนึ่งเราสามารถนับได้ 5 แถว (เริ่มต้นจาก 0) และใน 2 สถานที่ (เริ่มต้นจาก 0) ในสามเหลี่ยมของ Pascal - และมาถึงหมายเลข 10
ในวันที่สิบเอ็ดของคริสต์มาสสามเหลี่ยมมอบให้ฉัน ...
พลังของสิบเอ็ด
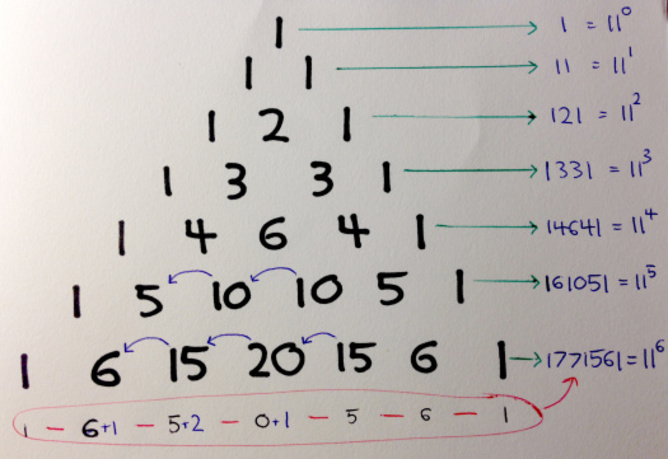
สำหรับเคล็ดลับปาร์ตี้ที่ยอดเยี่ยมโดยเฉพาะดูว่าเกิดอะไรขึ้นเมื่อคุณบีบตัวเลขทั้งหมดในแถวที่กำหนดด้วยกันเพื่อสร้างจำนวนมาก ที่จริงแล้วเราต้องระมัดระวังนิดหน่อยเมื่อต้องรับมือกับตัวเลขสองหลักและสิ่งที่คล้ายกัน-แทนที่จะเพียงแค่บีบพวกเขาเข้าด้วยกันเราจะย้ายตัวเลขพิเศษไปทางซ้าย (ในลักษณะที่คล้ายกับการเพิ่มโรงเรียนประถม)
ตัวอย่างเช่นเมื่อบีบแถว 1-4-6-4-1 เข้าด้วยกันเราเพิ่งจบลงด้วยหมายเลข 14641 แต่เมื่อเราบีบแถว 1-5-10-10-5-1 เข้าด้วยกันเราจะแยก 10S ออกเป็น 1 (ซึ่งเพิ่มจำนวนทางด้านซ้าย) และ 0 (ซึ่งอยู่)
เมื่อแยก 10 ครั้งแรกด้วยวิธีนี้แถวจะกลายเป็น 1- (5+1)-(0) -10-5-1 เมื่อ 10 ที่สองถูกแยกแถวจะจบลงเป็น 1- (5+1)-(0+1) -0-5-1 หรือ 1-6-1-0-5-1 และเราจบลงด้วยหมายเลข 161051 (มันง่ายกว่าที่จะอธิบายมันเชื่อใจฉัน!)
เช่นเดียวกับการรวมตัวเลขในแถวโดยการเพิ่มพวกเขาทำให้เรามีพลังของสองการรวมตัวเลขในแถวโดยการบีบพวกเขาเข้าด้วยกันเช่นนี้ทำให้เรามีพลังของสิบเอ็ด! โปรดทราบว่า 11 ถึงพลังของ 0 ต้องการที่จะเท่ากับ 1 เช่นกัน ...
ในวันที่สิบสองของคริสต์มาสสามเหลี่ยมให้ฉัน ...
เศษส่วนของ Sierpinski!

ตอนนี้สำหรับรูปแบบ Pascal ที่ชื่นชอบตลอดเวลาของฉัน-ฉันไม่เคยหยุดที่จะประหลาดใจกับวิธีที่ฉันชอบเศษส่วนสามเหลี่ยมตลอดเวลาซ่อนตัวอยู่ในสามเหลี่ยมของ Pascal ด้วย
สามเหลี่ยมของ Siepinskiเป็นรูปร่างที่คุณได้รับเมื่อคุณใช้รูปสามเหลี่ยมด้านเท่าตัดชิ้นกลางออกไปจากนั้นตัดชิ้นส่วนตรงกลางออกจากสามเหลี่ยมขนาดเล็กทั้งหมดที่เหลืออยู่จากนั้นไปตลอดไป (หรือจนกว่าคุณจะเหนื่อย)
สิ่งนี้เกี่ยวข้องกับสามเหลี่ยมของ Pascal อย่างไร? ดูว่าจะเกิดอะไรขึ้นเมื่อคุณแรเงาในตัวเลขคี่ทั้งหมดด้วยสีเดียวและตัวเลขทั้งหมดที่มีสีต่างกัน!
ขออวยพรให้คุณสุขสันต์วันคริสต์มาสและสวัสดีปีใหม่ ขอให้วันหยุดของคุณเต็มไปด้วยคณิตศาสตร์ที่สนุกสนานและเป็นกำลังใจที่ดี! และอาจมีนักคณิตศาสตร์ของคุณต่อจากนี้ไปโดยนักคณิตศาสตร์
Michael Rose ไม่ได้ทำงานให้คำปรึกษาหุ้นของตัวเองในหรือรับเงินทุนจาก บริษัท หรือองค์กรใด ๆ ที่จะได้รับประโยชน์จากบทความนี้และไม่มีส่วนเกี่ยวข้องที่เกี่ยวข้อง
บทความนี้เผยแพร่ครั้งแรกที่บทสนทนา- อ่านบทความต้นฉบับ-มุมมองที่แสดงเป็นของผู้เขียนและไม่จำเป็นต้องสะท้อนมุมมองของผู้จัดพิมพ์ บทความฉบับนี้ได้รับการเผยแพร่ครั้งแรกเมื่อLiveScience