สมการกำลังสองคืออะไร?

ในวิชาคณิตศาสตร์สมการกำลังสองเป็นปัญหาที่เกี่ยวข้องกับตัวแปรคูณด้วยตัวเอง - การดำเนินการที่เรียกว่ากำลังสอง ภาษานี้มาจากพื้นที่ของสี่เหลี่ยมเป็นความยาวด้านข้างคูณด้วยตัวเอง คำว่า "กำลังสอง" มาจากสี่เหลี่ยมคำละตินสำหรับสแควร์

สมการกำลังสองแสดงถึงปรากฏการณ์จำนวนมากในโลกแห่งความเป็นจริงเช่นที่เรือจรวดจะลงจอดได้เท่าไหร่ที่จะคิดค่าใช้จ่ายสำหรับผลิตภัณฑ์หรือระยะเวลาที่จะต้องใช้เวลานานเท่าไหร่ เนื่องจากการใช้งานที่หลากหลายของพวกเขา quadratics จึงมีความสำคัญทางประวัติศาสตร์อย่างลึกซึ้งและเป็นรากฐานของประวัติความเป็นมาของพีชคณิต-

พาราโบลา

คณิตศาสตร์ของจตุรัสมีความสัมพันธ์กับเส้นโค้งรูปตัวยูที่รู้จักกันในชื่อพาราโบลา บางทีตัวอย่างที่คุ้นเคยที่สุดคือกระแสของน้ำที่ยิงจากน้ำพุดื่ม มีตัวอย่างอื่น ๆ อีกมากมายเช่นหน้าตัดของจานดาวเทียมหรือสายเคเบิลบนสะพานแขวน

พาราโบลาเป็นรูปร่างที่สำคัญสำหรับนักคณิตศาสตร์หลายคนของกรีซโบราณเช่นลิดของอเล็กซานเดรีย (~ 300 ปีก่อนคริสตกาล) อาร์คิมีดีสแห่งซีราคิวส์ (287-212 ปีก่อนคริสตกาล) Apollonius แห่ง Perga (262-190 BC) นักวิชาการเหล่านี้ระบุคุณสมบัติทางคณิตศาสตร์จำนวนหนึ่งที่อยู่ภายในพาราโบลา:

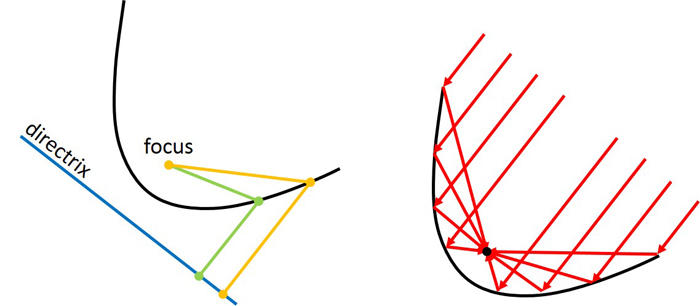
1. พาราโบลาเป็นชุดของคะแนนที่อยู่ห่างไกลจากจุด (กจุดสนใจ) และสาย (กDirectrix- จุดโฟกัสที่มีชื่ออย่างเหมาะสมมีความสำคัญในการใช้งานด้านวิศวกรรมสมัยใหม่หลายครั้งเนื่องจากเป็นจุดบนจานพาราโบลาในที่ที่มีการสะท้อนคลื่นที่เข้ามาไม่ว่าจะเป็นคลื่นวิทยุ (เช่นในจานดาวเทียม) แสง (เช่นในอาร์เรย์แสงอาทิตย์ที่เข้มข้น) หรือเสียง

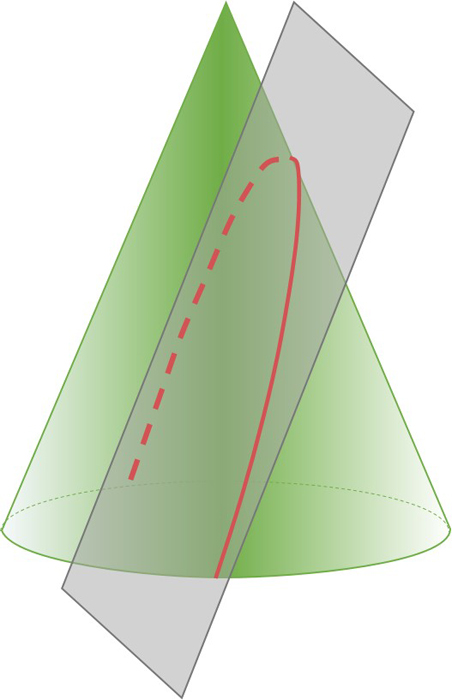
2. พาราโบลาถูกสร้างขึ้นโดยการตัดกรวยขนานกับความลาดชันของด้านข้างของกรวย ด้วยเหตุนี้พาราโบลาจึงอยู่ในชุดของเส้นโค้งคณิตศาสตร์ที่เรียกว่ารูปกรวย- เกือบ 2,000 ปีหลังจากการค้นพบครั้งนี้ในการวิจัยของเขาเกี่ยวกับ Parabolic "Burning Mirrors" Leonardo da Vinci (โฆษณา 1452-1519) เข้าใจทรัพย์สินนี้และพัฒนาเข็มทิศที่สามารถวาดพาราโบลา-

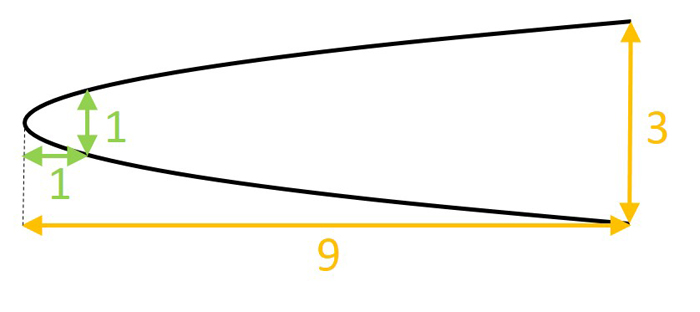
3. การเปลี่ยนแปลงความสูงของพาราโบลาเป็นสัดส่วนกับการเปลี่ยนแปลงในสี่เหลี่ยมจัตุรัสของความกว้างของพาราโบลานั้น ตัวอย่างเช่นหากพาราโบลาสูงหนึ่งหน่วยที่มีความกว้างหนึ่งหน่วยมันจะเป็นเก้า (สามกำลังสอง) ที่สูงซึ่งมีความกว้างสามหน่วย มาจากสถานที่ให้บริการนี้ที่ Apollonius ได้รับคำว่า "พาราโบลา" จากอุปมาคำภาษากรีกสำหรับ "แอปพลิเคชัน" ในแง่ที่ว่าความกว้างกำลังถูก "นำไปใช้กับ" (คูณด้วย) เอง นี่คือคุณสมบัติที่เชื่อมโยงรูปร่างของพาราโบลากับแนวคิดทางคณิตศาสตร์ของสมการกำลังสอง

แม้ว่าพาราโบลาจะแพร่หลาย แต่ก็เป็นสิ่งสำคัญที่จะต้องทราบว่าพวกเขาแตกต่างจากเส้นโค้งรูปตัวยูอื่น ๆ เช่นโซ่แขวน (เป็นโซ่) เส้นทางของเด็กบนแกว่ง (โค้งวงกลม) ส่วนโค้งจากไฟฉายตั้งตรงบนผนัง (ไฮเปอร์โบลา) เส้นโค้งอื่น ๆ เหล่านี้ไม่มีคุณสมบัติที่กล่าวถึงก่อนหน้านี้ของพาราโบลา

การเคลื่อนไหวของกระสุนปืน

การเชื่อมโยงระหว่างพาราโบลาและคณิตศาสตร์ของสี่เหลี่ยมจัตุรัสมีความสำคัญอย่างยิ่งในโฆษณาศตวรรษที่ 16 เมื่อนักวิชาการของยุคฟื้นฟูศิลปวิทยายุโรปสังเกตเห็นว่าขีปนาวุธเช่นลูกกระสุนปืนใหญ่และครกเดินทางไปในวิถีพาราโบลา นักวิทยาศาสตร์ที่มีชื่อเสียงหลายคนในยุคนั้นรวมถึง Leonardo da Vinci และ Galileo Galilei (1564-1642) ศึกษาศึกษาการเคลื่อนไหวของกระสุนปืน- ตามที่โจเซฟดับบลิว Dauben ศาสตราจารย์ด้านประวัติศาสตร์ที่มหาวิทยาลัยเมืองนิวยอร์ก (CUNY) เพราะศิลปินแห่งยุคฟื้นฟูศิลปวิทยาการเริ่มหมกมุ่นอยู่กับความเป็นจริงที่แสดงให้เห็นอย่างถูกต้องในงานศิลปะกาลิเลโอก็หมกมุ่นอยู่กับความเป็นจริงอย่างแม่นยำในทำนองเดียวกันโดยใช้ คณิตศาสตร์- ในปี 1638 กาลิเลโอที่ตีพิมพ์ครั้งแรกการพิสูจน์การเร่งความเร็วที่สม่ำเสมอจากแรงโน้มถ่วงของโลกจะทำให้ขีปนาวุธเคลื่อนที่ในวิถีพาราโบลา คณิตศาสตร์นั้นสามารถใช้เพื่ออธิบายการเคลื่อนไหวเป็นกุญแจสำคัญต่อความก้าวหน้าของการปฏิวัติทางวิทยาศาสตร์

กราฟของจตุรัส

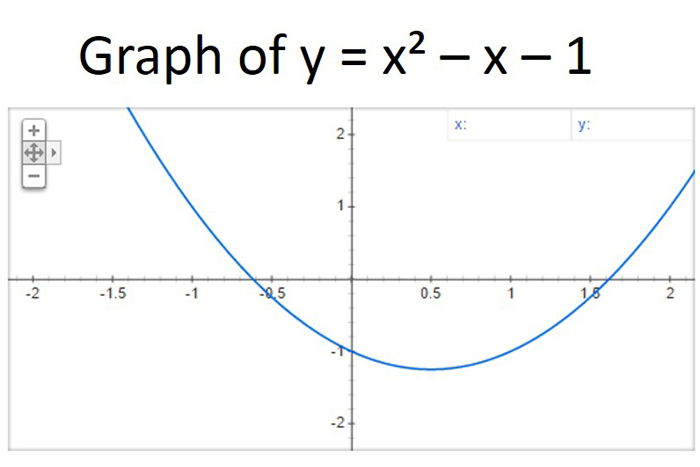
ในเวลาเดียวกันกับกาลิเลโอนักปรัชญาชาวฝรั่งเศสและนักคณิตศาสตร์René Descartes (1596-1650) ตีพิมพ์“ La Géométrie” (1637) ซึ่งอธิบายถึงเทคนิคของสมการพีชคณิตกราฟในสาขาที่เรียกว่าเรขาคณิตวิเคราะห์ การเปลี่ยนแปลงของวิธีการของเขายังคงใช้อยู่ในปัจจุบัน ดังที่แสดงไว้ด้านล่างกราฟของสมการกำลังสองคือพาราโบลา

สมการโบราณโบราณ: อัตราส่วนทองคำ

เพื่อทำความเข้าใจวิธีการแก้สมการกำลังสองที่นักคณิตศาสตร์นักวิทยาศาสตร์และวิศวกรใช้วันนี้ลองสำรวจปัญหาคณิตศาสตร์โบราณ: อัตราส่วนทองคำ ในขณะที่อยู่ใน "ความเข้าใจผิดเกี่ยวกับอัตราส่วนทองคำ"(1992), George Markowsky ศาสตราจารย์คณิตศาสตร์ที่ University of Maine ชี้ให้เห็นว่าความสำคัญทางประวัติศาสตร์ของอัตราส่วนทองคำและการดึงดูดความงามมักจะเกินจริงแม้ว่ามันจะเป็นจริงลำดับ Fibonacci), เรขาคณิต (เช่นในicosahedron) และชีววิทยา (เช่นมุมระหว่างใบพืช-

วิธีการหนึ่งในการกำหนดอัตราส่วนทองคำจึงมีการระบุไว้:

ค้นหาสี่เหลี่ยมผืนผ้าที่มีความยาวและความกว้างเช่นเมื่อสี่เหลี่ยมถูกตัดออกจากปลายด้านหนึ่งของสี่เหลี่ยมผืนผ้าเศษสี่เหลี่ยมเศษซากที่เหลือจะมีรูปร่างหรือ "อัตราส่วนภาพ" เหมือนสี่เหลี่ยมเดิม (แต่หมุนที่มุมขวา)

ในขณะที่ชาวกรีกโบราณแก้ปัญหานี้ใช้เรขาคณิตเราจะใช้พีชคณิตตามที่ได้รับการสอนในวันนี้

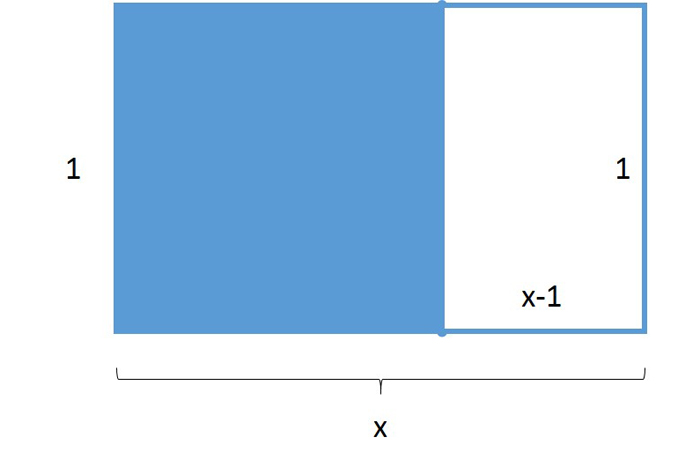
ในการพิจารณาความยาวและความกว้างที่จะสร้างอัตราส่วนทองคำเราให้ความยาวด้านสั้น 1 และความยาวด้านยาวของ x เนื่องจากอัตราส่วนภาพถูกกำหนดเป็นด้านยาวหารด้วยด้านสั้นอัตราส่วนภาพสำหรับสี่เหลี่ยมนี้คือ x/1 หรือเพียงแค่ x ถ้าเราตัดสี่เหลี่ยมออกจากสี่เหลี่ยมนี้เศษเหล็กที่เหลือจะมีความยาวด้านยาว 1 และความยาวด้านสั้น ๆ ของ x-1 ดังนั้นอัตราส่วนภาพคือ 1/(x-1) การทำความเข้าใจว่าอัตราส่วนภาพสำหรับสี่เหลี่ยมผืนผ้าโดยรวมและสี่เหลี่ยมเศษเล็กเศษน้อยควรเหมือนกันสมการของเราคือ x = 1/(x - 1)

สูตรกำลังสอง

นี่คือวิธีที่นักเรียนได้รับคำสั่งให้แก้สมการนี้ในวันนี้ เริ่มต้นด้วยสมการ:

x = 1/(x - 1)

คูณแต่ละด้านของสมการด้วยนิพจน์ x - 1:

x · (x - 1) = 1

แจกจ่าย X ข้ามนิพจน์ x - 1:

x · x - x · 1 = 1

ตัวแปร x คูณด้วยตัวเองเขียนเป็นx² การยกกำลังนี้คือสิ่งที่ทำให้สมการเป็นกำลังสอง:

x² - x = 1

ตอนนี้เราลบ 1 จากแต่ละด้านของสมการเพื่อให้บรรลุสิ่งที่เรียกว่ารูปแบบมาตรฐานของสมการกำลังสอง:

x² - x - 1 = 0

อย่างเท่าเทียมกันนี้อาจเขียนเป็น:

(1) ·x² + (-1) · x + (-1) = 0

เมื่อเปรียบเทียบกับสมการ A ·X² + B · X + C = 0 มันจะให้ค่าของ A = 1, B = -1 และ C = -1 ค่าเหล่านี้ใช้ในสูตรกำลังสองเป็น

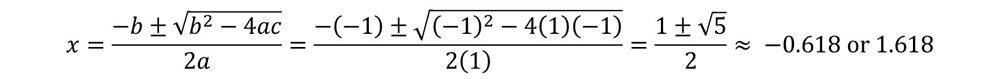
สัญลักษณ์ "±" หมายถึง "บวกหรือลบ" ด้วยเหตุนี้สูตรกำลังสองจึงให้สองวิธีแก้ปัญหาเสมอ แทนที่ค่าเหล่านี้อย่างใดอย่างหนึ่งลงในสมการ x = 1/(x - 1) เพื่อทดสอบว่าสิ่งนี้ทำให้ทั้งสองด้านของสมการออกมาเหมือนกันหรือไม่ มันหมายถึงวิธีการทำงาน สังเกตค่าเหล่านี้ยังเป็นสถานที่ที่กราฟของรูปแบบมาตรฐานของสมการ (y = x² - x - 1) ข้ามแกน x ซึ่งอยู่ที่ y = 0 (ดูกราฟด้านบน) ในกรณีนี้ค่าบวกมีความสำคัญทางกายภาพมากขึ้นเนื่องจากสี่เหลี่ยมไม่ควรมีความกว้างเชิงลบ

ต้นกำเนิดของบาบิโลนโบราณ

เพื่อให้ข้อมูลเชิงลึกเกี่ยวกับที่สูตรกำลังสองมาจากไหนและทำไมมันทำงานให้เราตรวจสอบขั้นตอนที่ใช้บนแท็บเล็ตดินเหนียวบาบิโลนโบราณจากประมาณ 1800 ปีก่อนคริสตกาล (แท็บเล็ตBM 13901, พิพิธภัณฑ์บริติช) ตามที่ Jacques Sesiano ใน "การแนะนำประวัติของพีชคณิต"(AMS, 2009) ปัญหาแรกของแท็บเล็ตนี้แปลโดยประมาณ:

ฉันเพิ่มพื้นที่และด้านข้างของสี่เหลี่ยมเพื่อรับ¾ ด้านข้างของสี่เหลี่ยมคืออะไร?

ปัญหาเขียนขึ้นในสัญกรณ์สมัยใหม่เป็น:

x² + x = ¾

ต่อไปนี้เป็นวิธีการเล่าขานของวิธีการบาบิโลนและอาหรับตามที่อธิบายโดยเซเซียโน ก่อนอื่นเราจะแปลขั้นตอนที่ชาวบาบิโลนใช้ แต่ยังแปลพวกเขาเป็นภาษาสัญลักษณ์ที่เราใช้ในวันนี้ในพีชคณิต ภาษาสัญลักษณ์อย่างเต็มที่ปรากฏตัวครั้งแรกในยุโรปในศตวรรษที่ 17 เนื่องจากชาวบาบิโลนไม่ทราบเกี่ยวกับจำนวนลบจึงจำเป็นต้องเขียนสมการในรูปแบบ x²+ px = q โดยที่ p = 1 และ q = ¾ เมื่อเปรียบเทียบสิ่งนี้กับขวานรูปแบบมาตรฐานที่ทันสมัย²& + bx + c = 0 แสดงว่า p = b/a และ q = -c/a

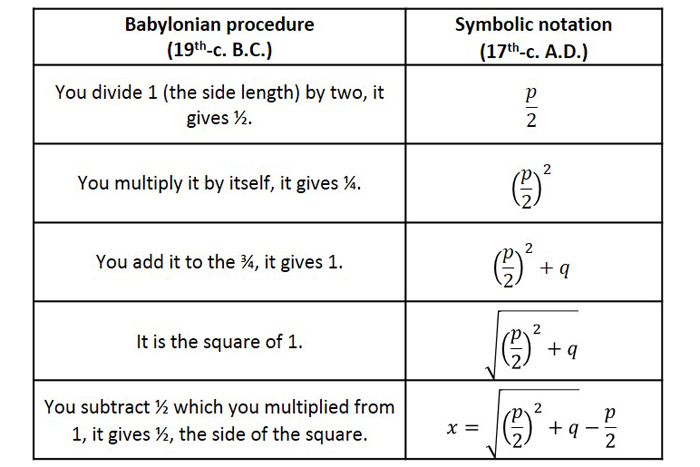
ตอนนี้เรามาหาและพิสูจน์ขั้นตอนนั้นถูกต้องโดยใช้วิธีการเรขาคณิตตามที่นักคณิตศาสตร์อาหรับทำในโฆษณาในศตวรรษที่เก้าต่อไปนี้เป็นรูปแบบของการพิสูจน์ที่ปรากฏในนักคณิตศาสตร์ชาวเปอร์เซียอัล-khwārizmīการตีพิมพ์ของ "หนังสือที่ถูกต้องตามการคำนวณ ปรากฏขึ้นจนถึงยุคทองของศาสนาอิสลามระยะเวลาตั้งแต่กลางศตวรรษที่สิบเจ็ดถึงกลางศตวรรษที่ 13 เมื่อชาวมุสลิมปกครองอาณาจักรที่ทอดยาวจากเอเชียกลางไปยังแอฟริกาเหนือและไอบีเรีย

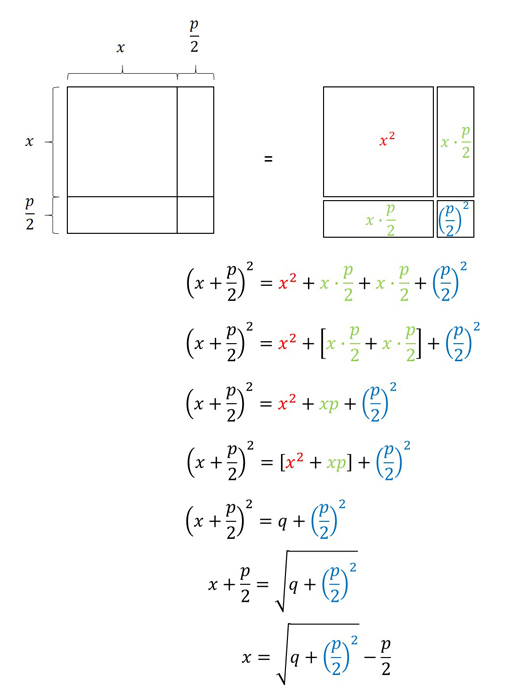
ถ้าเรา "เสียบ" p = b/a และ q = -c/a สูตรจะลดความซับซ้อนให้กับรูปแบบที่ทันสมัยของสมการกำลังสองเท่าที่ได้รับการสอนในวันนี้

รูปแบบต่าง ๆ ของสูตรกำลังสองถูกนำมาใช้ทั่วทั้งแอฟริกา-ยูราเซียในช่วงอายุ ชาวบาบิโลนและชาวอียิปต์ใช้เวอร์ชั่นขั้นตอนในช่วงศตวรรษที่ 19 ชาว Chaldeans ในศตวรรษที่สิบเจ็ดก่อนคริสต์ศักราชชาวกรีกในศตวรรษที่สี่และชาวอินเดียในศตวรรษที่ 11 รูปแบบการใช้งานของอาหรับ อารยธรรมคืบหน้ามากขึ้นเมื่อเรียนรู้เกี่ยวกับตัวเลขเชิงลบไม่มีเหตุผลจินตนาการและซับซ้อน

ทรัพยากรเพิ่มเติม

• Drexel University มีหน้าเว็บที่ให้ความบันเทิงซึ่งแสดงให้เห็นถึงประวัติความเป็นมาของกราฟ-
• PurpleMath.com เว็บไซต์บทเรียนคณิตศาสตร์อธิบายรูปกรวยและพาราโบลา-
• MathWorld ทรัพยากรคณิตศาสตร์ออนไลน์กล่าวถึงสมการกำลังสอง-