ลำดับฟีโบนัชชีเป็นลำดับทางคณิตศาสตร์ที่มีชื่อเสียง โดยแต่ละตัวเลขคือผลรวมของตัวเลขสองตัวก่อนหน้า ผู้คนอ้างว่ามีคุณสมบัติพิเศษมากมายเกี่ยวกับลำดับตัวเลข เช่น ความจริงที่ว่ามันเป็น “รหัสลับของธรรมชาติ” สำหรับการสร้างโครงสร้างที่สมบูรณ์แบบ เช่นมหาปิรามิดที่กิซ่าหรือเปลือกหอยอันเป็นเอกลักษณ์ที่น่าจะประดับปกโรงเรียนของคุณคณิตศาสตร์หนังสือเรียน แต่ส่วนใหญ่นั้นเป็นตำนานมากกว่าข้อเท็จจริง และประวัติศาสตร์ที่แท้จริงของซีรีส์นี้ก็มีความลึกซึ้งมากกว่านั้นเล็กน้อย
อธิบายลำดับฟีโบนัชชี
ลำดับฟีโบนัชชีคือชุดตัวเลขซึ่งแต่ละตัวเลขคือผลรวมของตัวเลขสองตัวที่อยู่ข้างหน้า เริ่มต้นที่ 0 และ 1 ตัวเลข 10 แรกของลำดับจะมีลักษณะดังนี้ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 และต่อๆ ไปตลอดไป
ลำดับฟีโบนัชชีสามารถอธิบายได้โดยใช้สมการทางคณิตศาสตร์: Xn+2= เอ็กซ์n+1+ เอ็กซ์n
ประวัติลำดับฟีโบนัชชี
สิ่งแรกที่ต้องรู้คือลำดับนี้ไม่ใช่ลำดับฟีโบนัชชีแต่เดิม ซึ่งจริงๆ แล้วไม่เคยใช้ชื่อนั้นเลย นักคณิตศาสตร์ชาวอิตาลีที่เราเรียกว่า Leonardo Fibonacci เกิดประมาณปี 1170 และเดิมรู้จักกันในชื่อ Leonardo of Pisa Keith Devlin นักคณิตศาสตร์จากมหาวิทยาลัยสแตนฟอร์ดกล่าว
เฉพาะในศตวรรษที่ 19 นักประวัติศาสตร์เท่านั้นที่ตั้งชื่อเล่นว่าฟีโบนัชชี (ความหมายคร่าวๆ ว่า "บุตรแห่งตระกูลโบนักชี") เพื่อแยกแยะนักคณิตศาสตร์คนนี้จากที่อื่นเลโอนาร์โด้แห่งปิซาผู้โด่งดังเดฟลินกล่าว
อ่านเพิ่มเติม:ตัวเลขขนาดใหญ่ที่กำหนดจักรวาล
เลโอนาร์โดแห่งปิซาไม่ได้ค้นพบลำดับดังกล่าวจริงๆ เดฟลิน ผู้เขียนเรื่อง "Finding Fibonacci: The Quest to Rediscover the Forgotten Mathematical Genius Who Changed the World" กล่าว (สำนักพิมพ์มหาวิทยาลัยพรินซ์ตัน, 2017) ข้อความสันสกฤตโบราณที่ใช้ระบบเลขฮินดู-อารบิกกล่าวถึงสิ่งนี้ครั้งแรกใน 200 ปีก่อนคริสตกาลก่อนเลโอนาร์โดแห่งปิซาหลายศตวรรษ
“มันเป็นเช่นนั้นตลอดไป” เดฟลินบอกกับ WordsSideKick.com
อย่างไรก็ตาม ในปี 1202 เลโอนาร์โดแห่งปิซาได้ตีพิมพ์หนังสือเล่มใหญ่ "Liber Abaci" ซึ่งเป็น "ตำราอาหารทางคณิตศาสตร์สำหรับวิธีคำนวณ" เดฟลินกล่าว "Liber Abaci" เขียนขึ้นสำหรับพ่อค้า โดยเป็นโครงร่างเลขคณิตฮินดู-อารบิกที่มีประโยชน์ในการติดตามผลกำไร การขาดทุน ยอดเงินกู้คงเหลือ และอื่นๆ เขากล่าวเสริม
ในที่แห่งหนึ่งในหนังสือ Leonardo of Pisa แนะนำลำดับที่มีปัญหาที่เกี่ยวข้องกระต่าย- ปัญหาเกิดขึ้นดังนี้ เริ่มจากกระต่ายตัวผู้และกระต่ายตัวเมีย หลังจากผ่านไปหนึ่งเดือน พวกมันจะโตเต็มที่และออกลูกร่วมกับกระต่ายตัวผู้และตัวเมียอีกตัวหนึ่ง หนึ่งเดือนต่อมา กระต่ายเหล่านั้นผสมพันธุ์และออกมา คุณคงเดาได้ว่าเป็นตัวผู้และตัวเมียอีกตัวที่สามารถผสมพันธุ์ได้หลังจากผ่านไปหนึ่งเดือน (ละเว้นสิ่งที่ไม่น่าจะเป็นไปได้อย่างมากชีววิทยาที่นี่.) หนึ่งปีผ่านไป คุณจะมีกระต่ายกี่ตัว?
ปรากฎว่าคำตอบคือ 144 และสูตรที่ใช้เพื่อให้ได้คำตอบนั้นคือสิ่งที่ปัจจุบันเรียกว่าลำดับฟีโบนักชี
อ่านเพิ่มเติม:9 สมการที่เปลี่ยนโลก
"Liber Abaci" เปิดตัวซีเควนซ์นี้สู่โลกตะวันตกเป็นครั้งแรก แต่หลังจากอ่านเพียงไม่กี่ย่อหน้าเกี่ยวกับการเพาะพันธุ์กระต่าย เลโอนาร์โดแห่งปิซาก็ไม่เคยพูดถึงลำดับนี้อีกเลย ในความเป็นจริง ส่วนใหญ่จะถูกลืมไปจนกระทั่งศตวรรษที่ 19 เมื่อนักคณิตศาสตร์ค้นคว้าเพิ่มเติมเกี่ยวกับคุณสมบัติทางคณิตศาสตร์ของลำดับดังกล่าว ในปี พ.ศ. 2420 เอดูอาร์ด ลูคัส นักคณิตศาสตร์ชาวฝรั่งเศสได้ตั้งชื่อปัญหากระต่ายอย่างเป็นทางการว่า "ลำดับฟีโบนัชชี" เดฟลินกล่าว
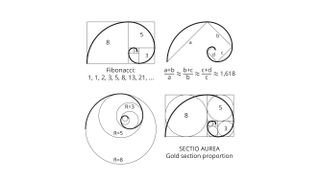
ลำดับฟีโบนัชชีและอัตราส่วนทองคำ
นอกเหนือจากการเป็นเครื่องมือในการสอนที่ดีแล้ว ลำดับฟีโบนักชียังปรากฏอยู่ในธรรมชาติบางแห่งอีกด้วย อย่างไรก็ตาม ไม่ใช่รหัสลับบางอย่างที่ควบคุมสถาปัตยกรรมของจักรวาลเดฟลินกล่าว
เป็นเรื่องจริงที่ลำดับฟีโบนัชชีมีความเชื่อมโยงอย่างแน่นหนากับสิ่งที่ปัจจุบันรู้จักกันในชื่อนี้อัตราส่วนทองคำพี, หนึ่งจำนวนอตรรกยะที่มีตำนานที่น่าสงสัยมากมายในตัวมันเอง อัตราส่วนของตัวเลขต่อเนื่องในลำดับฟีโบนัชชีจะเข้าใกล้อัตราส่วนทองคำมากขึ้น ซึ่งก็คือ 1.6180339887498948482...
อ่านเพิ่มเติม:9 ตัวเลขที่มีมวลมากที่สุดที่มีอยู่
อัตราส่วนทองคำสามารถจับการเจริญเติบโตของพืชบางประเภทได้ Devlin กล่าว ตัวอย่างเช่น การจัดเรียงใบหรือกลีบเป็นเกลียวบนต้นไม้บางชนิดเป็นไปตามอัตราส่วนทองคำ โคนต้นสนมีลักษณะเป็นเกลียวสีทอง เช่นเดียวกับเมล็ดในดอกทานตะวัน "Phyllotaxis: การศึกษาเชิงระบบในการสร้างสัณฐานวิทยาของพืช" (สำนักพิมพ์มหาวิทยาลัยเคมบริดจ์, 1994) แต่มีพืชหลายชนิดที่ไม่ปฏิบัติตามกฎนี้
“ไม่ใช่ 'กฎข้อเดียวของพระเจ้า' สำหรับการเจริญเติบโตของสิ่งต่าง ๆ ขอให้เป็นอย่างนั้น” เดฟลินกล่าว

ลำดับฟีโบนัชชีในธรรมชาติและสถาปัตยกรรม
บางทีตัวอย่างที่มีชื่อเสียงที่สุดก็คือ เปลือกหอยที่รู้จักกันในชื่อหอยโข่งที่จริงแล้วไม่ได้เติบโตใหม่เซลล์ตามลำดับฟีโบนัชชี เขากล่าวเสริม เมื่อผู้คนเริ่มเชื่อมโยงถึงร่างกายมนุษย์ศิลปะและสถาปัตยกรรม ลิงก์ไปยังลำดับฟีโบนัชชีเปลี่ยนจากเรื่องเล็กน้อยไปสู่เรื่องสมมติอย่างจริงจัง
“คงต้องใช้หนังสือเล่มใหญ่เล่มหนึ่งเพื่อบันทึกข้อมูลที่ผิดทั้งหมดเกี่ยวกับอัตราส่วนทองคำ ซึ่งส่วนใหญ่เป็นเพียงการทำซ้ำข้อผิดพลาดเดียวกันโดยผู้เขียนคนละคน” George Markowsky นักคณิตศาสตร์ซึ่งขณะนั้นอยู่ที่มหาวิทยาลัย Maineเขียนในรายงานปี 1992ในวารสารคณิตศาสตร์วิทยาลัย
ข้อมูลที่ผิดส่วนใหญ่มาจากหนังสือปี 1855 โดยนักจิตวิทยาชาวเยอรมัน Adolf Zeising ที่เรียกว่า "Aesthetic Research" Zeising อ้างว่าสัดส่วนของร่างกายมนุษย์ขึ้นอยู่กับอัตราส่วนทองคำ ในปีต่อๆ มา อัตราส่วนทองคำได้ก่อให้เกิด "สี่เหลี่ยมสีทอง" "สามเหลี่ยมทองคำ" และทฤษฎีต่างๆ มากมายเกี่ยวกับที่มาของมิติอันเป็นสัญลักษณ์เหล่านี้
ตั้งแต่นั้นมา ผู้คนต่างกล่าวว่าอัตราส่วนทองคำสามารถพบได้ในมิติของพีระมิดที่กิซ่า วิหารพาร์เธนอนเลโอนาร์โด ดา วินชีของ "วิทรูเวียนแมน" และฝูงของยุคฟื้นฟูศิลปวิทยาอาคาร การกล่าวอ้างที่ครอบคลุมเกี่ยวกับอัตราส่วนที่ "น่าพึงพอใจเป็นพิเศษ" ต่อสายตามนุษย์นั้น ได้รับการระบุไว้อย่างไม่มีวิจารณญาณ Devlin กล่าว คำกล่าวอ้างทั้งหมดนี้เมื่อได้รับการทดสอบแล้ว ถือเป็นความเท็จที่สามารถวัดผลได้ เขากล่าวเสริม
“เราเป็นผู้จดจำรูปแบบที่ดี เราสามารถเห็นรูปแบบได้ไม่ว่าจะมีหรือไม่ก็ตาม” เดฟลินกล่าว “ทั้งหมดเป็นเพียงความปรารถนา”
หมายเหตุบรรณาธิการ: Adam Mann มีส่วนร่วมในบทความนี้-
เผยแพร่ครั้งแรกบน WordsSideKick.com-