经过三十年的寻找,数学家们并没有被吓倒,在超级计算机的帮助下,终于发现了一个特殊整数的新例子,称为戴德金数。
如果您要更新自己的记录,则仅是此类的第九个或 D(9),计算结果等于 286 386 577 668 298 411 128 469 151 667 598 498 812 366。 这个 42 位数字的怪物沿袭了 1991 年发现的 23 位数字 D(8)。
对于非数学家来说,掌握戴德金数的概念很困难,更不用说计算出来了。 事实上,所涉及的计算是如此复杂,涉及的数字如此之大,以至于无法确定 D(9) 是否会被发现。
“32 年来,D(9) 的计算一直是一个公开的挑战,是否能够计算出这个数字值得怀疑,”说德国帕德博恩大学的计算机科学家 Lennart Van Hirtum 于 6 月宣布这一数字。
戴德金数的中心是布尔函数,或一种从仅由两个状态组成的输入中选择输出的逻辑,例如 true 和 false,或 0 和 1。
单调布尔函数是那些限制逻辑的函数,即在输入中将 0 换成 1 只会导致输出从 0 变为 1,而不是从 1 变为 0。
研究人员形容它使用红色和白色而不是 1 和 0,但想法是相同的。
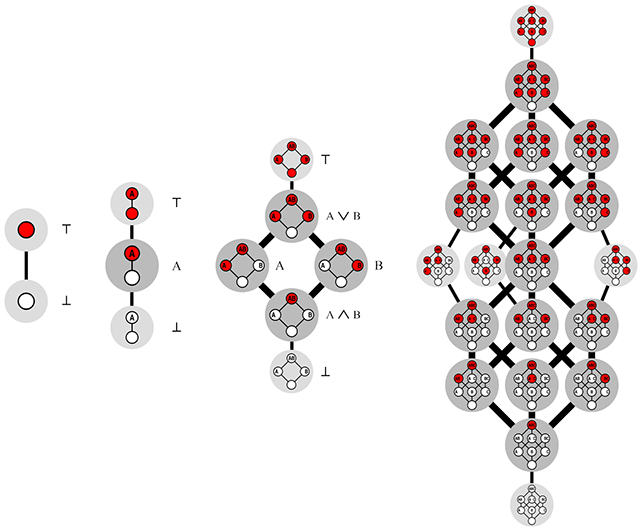
“基本上,你可以将二维、三维和无限维中的单调布尔函数视为具有 n 维立方体的游戏,”说范赫图姆.
“你平衡立方体的一个角,然后将剩余的每个角涂成白色或红色。”
“只有一个规则:你绝对不能将白色角放在红色角之上。这会创建一种垂直的红白交叉点。游戏的目的是计算有多少种不同的切割。”
前几个非常简单。 数学家将 D(1) 算作 2,然后是 3、6、20、168 ?
早在 1991 年,就花了Cray-2超级计算机(当时最强大的超级计算机之一)和数学家 Doug Wiedemann 花了 200 个小时才算出 D(8)。
D(9) 的长度几乎是 D(8) 的两倍,并且需要一种特殊的超级计算机:使用称为现场可编程门阵列 (FPGA) 的专用单元,可以并行处理多个计算。 于是,团队开发了帕德博恩大学的 Noctua 2 超级计算机。
“用 FPGA 解决硬组合问题是一个很有前景的应用领域,Noctua 2 是全球为数不多的可以进行实验的超级计算机之一。”说计算机科学家 Christian Plessl,Noctua 2 所在的帕德博恩并行计算中心 (PC2) 的负责人。
需要进一步优化才能让 Noctua 2 发挥作用。 利用公式中的对称性使过程更加高效,研究人员给超级计算机计算了一笔巨款,这笔金额涉及 5.5*10^18 项(地球上沙粒的数量估计为 7.5*10^ 18,用于比较)。
五个月后,Noctua 2 给出了答案,我们现在有了 D(9)。 研究人员暂时没有提及D(10) ? 但我们可以想象,可能还需要 32 年才能找到它。
该论文于 9 月在布尔函数及其应用国际研讨会(博鳌亚洲论坛)在挪威。
本文的早期版本首次发布于 2023 年 6 月。