大数量无处不在,从人体的细胞到宇宙的大小。但是,一旦数字超越了身体的领域,人类的思想就可以努力掌握这些数字的绝妙规模。相比之下,即使是无穷大似乎也更容易理解 - 它不断。一旦数字开始变得足够大,一切都开始变得模糊了,晚了乔恩·博威(Jon Borwein)曾是澳大利亚纽卡斯尔大学的应用数学家,他于2013年告诉Live Science。
“我们不理解这个规模的数字,”博威恩说。
从谦虚的万亿到格雷厄姆的数字,这里有一些最令人难以置信的数字。
大是相对的

考虑个人预算时31.4万亿美元的债务上限是不可想象的。但是,根据宇宙中原子的规模,相比之下,它看起来绝对是微不足道的,斯科特·亚伦森(Scott Aaronson)是一名计算机科学家,前身是麻省理工学院(MIT),现在在德克萨斯大学奥斯汀分校(University of Dexas Oustin)在奥斯汀分校(University of Dexkas of Dexas Austin)告诉Live Science。
有关的:可观察到的宇宙中有多少个原子?
为了了解大量数字,大多数人都依靠规模的类比。例如,卡尔·萨根(Carl Sagan)将宇宙年龄比作一个日历年,人类仅在除夕的最后几个小时出现。
Riemann假设
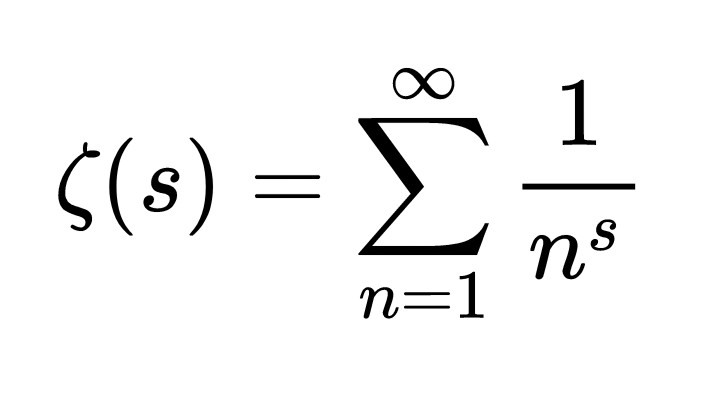
1859年首次说明Riemann假设是数学最伟大的猜想之一,无论谁解决的人都将获得100万美元的奖金。假设是,特定函数的每个非平凡零的实际部分(恰当地命名为riemann zeta函数)为1/2。
Borwein说:“这是数学中最大的开放问题,它将保证您的名字在10,000年内已知。”
该假设(如果为true)对质数的分布具有重要意义,而这些分布除了本身或一个人以外的任何事物都无法排除。他说,为了检验假设,数学家正在寻找极大的素数 - 大约大约有10个大约30的力量的素数。 Borwein说,这听起来可能是抽象的,但它具有许多现实世界的影响。他说:“素数已嵌入我们用于加密的所有内容中。” “所有这些都依赖于使用我们认为是真实但不知道的素数的属性设计算法设计的东西。”
宇宙

早在阿基米德(Archimedes),哲学家就想知道有多少个小粒子可以适合宇宙。阿基米德(Archimedes)估计,大约有10粒沙子的力量可以填充宇宙。他使用了一系列极为粗糙的估计 - 罂粟种子会产生一粒沙子,覆盖体育场长度的沙粒以及地球和太阳之间的体育场长度。亨利·孟德尔,洛杉矶加利福尼亚州立大学的古典历史学家。
尽管他采取了粗暴的措施,但他并没有太远。当前的估计值使宇宙中的原子总数约为10到82。
宇宙学因素

当爱因斯坦想到了他的方程式相对论,他包括一个小常数,称为宇宙常数,说明宇宙是静止的事实。尽管他后来在得知宇宙正在扩展时取消了常数,但事实证明,天才可能已经发生了事情:科学家认为,宇宙学的常数仅为减去122的力量仅10个,这揭示了黑暗能量的线索,这些线索神秘地加速了宇宙,Aaronson在2013年告诉现场科学。
宇宙学常数对于科学家来说是一个巨大的头痛,因为预测与常数的测量差异120个数量级不同,多年来,物理学家试图通过调整其他元素来解释这种差异,例如粒子质量如何随时间变化,时间如何变化,现场科学先前报道。
大力神和九头蛇

有时候,事情必须变得很大,然后才变得很小。 1982年,数学家杰夫·巴黎(Jeff Paris)和劳里·柯比(Laurie Kirby)摆谜:想象一下,大力神与一种像树一样长的hydra作斗争。如果他切断了一个头,那么神话怪物只是逐渐恢复了一些由几个规则支配的头部。令人惊讶的是,赫拉克勒斯最终将始终对九头蛇占上风,并砍掉所有Hydra的头部。
但是,即使大力神很聪明,并且选择了最有效的策略,Hydra也会首先生长的速度超过了谷歌的头(或提高10升至100功率的功率)。
梅森·普里姆(Mersenne Primes)

梅森·普里姆(Mersenne Primes)是一类急忙的数字。这些质数等于质量数减去1的功率的2个升高。而前几个开始小-3、7、31,它们爆炸以非常快地变得非常大。直到1951年左右,其中只有12个素数已知,但到今年(2024年),有52个已知。
为了通过这些巨大的数字为动力,科学家使用了出色的Internet Mersenne Primes搜索(GIMP),该搜索使用数千个互联网用户的计算能力来搜索难以捉摸的质数。这最大的已知质数由业余研究员和前NVIDIA员工卢克·杜兰特(Luke Durant)于2024年10月发现。数字2136,279,841- 1,拥有高达41,024,320位数字,比以前的唱片持有人多1600万位数字,六年前Gimps也发现了纪录持有人。
一万亿个三角形
大约1000年前,波斯数学家Al Karaji首先问存在多少个一致数字。但是什么是一致的数字?这些数字是具有整数或分数长的右角三角形的区域。因此,一个长度为3,4和5的三角形的面积为½ * 3 * 4 = 6,使6个全一个数字。
在发现前一百个一致数字之前,又花了几千年。到2009年,超级计算机已经发现了前3,148,379,694个同等数字。其中一些数字是如此巨大,以至于它们的数字以十进制形式写出,它们会延伸到月球和后背。 Borwein说,巨大的数字在数据存储中具有有趣的含义,因为它们是如此巨大,以至于流浪伽玛射线可以破坏这些数字的位置并使它们错误。
格雷厄姆的电话号码

与格雷厄姆(Graham)的数字相比,所有这些数字都苍白,这个数字如此之大,以至于仅仅试图记住所有数字就会将您的头变成一个黑洞。这个数字在数学证明中是有史以来最大的数字,是为了响应一个简单的谜语,讲述了如何将人们分配给具有一些约束的某些委员会。
尽管数学家有信心解决这个问题,但在1970年代,数学家和杂耍演员罗纳德·格雷厄姆(Ronald Graham)推测,必须低于格雷厄姆的人数。简单地计算数字将需要64个步骤,涉及乘以大量的3s。
没有办法使用科学符号编写数字,而必须用一系列的向上箭头书写,以表示指数的塔。后来,格雷厄姆(Graham)表明,这个谜语的上限比格雷厄姆(Graham)的数字小得多,但仍然很大。
树(3)
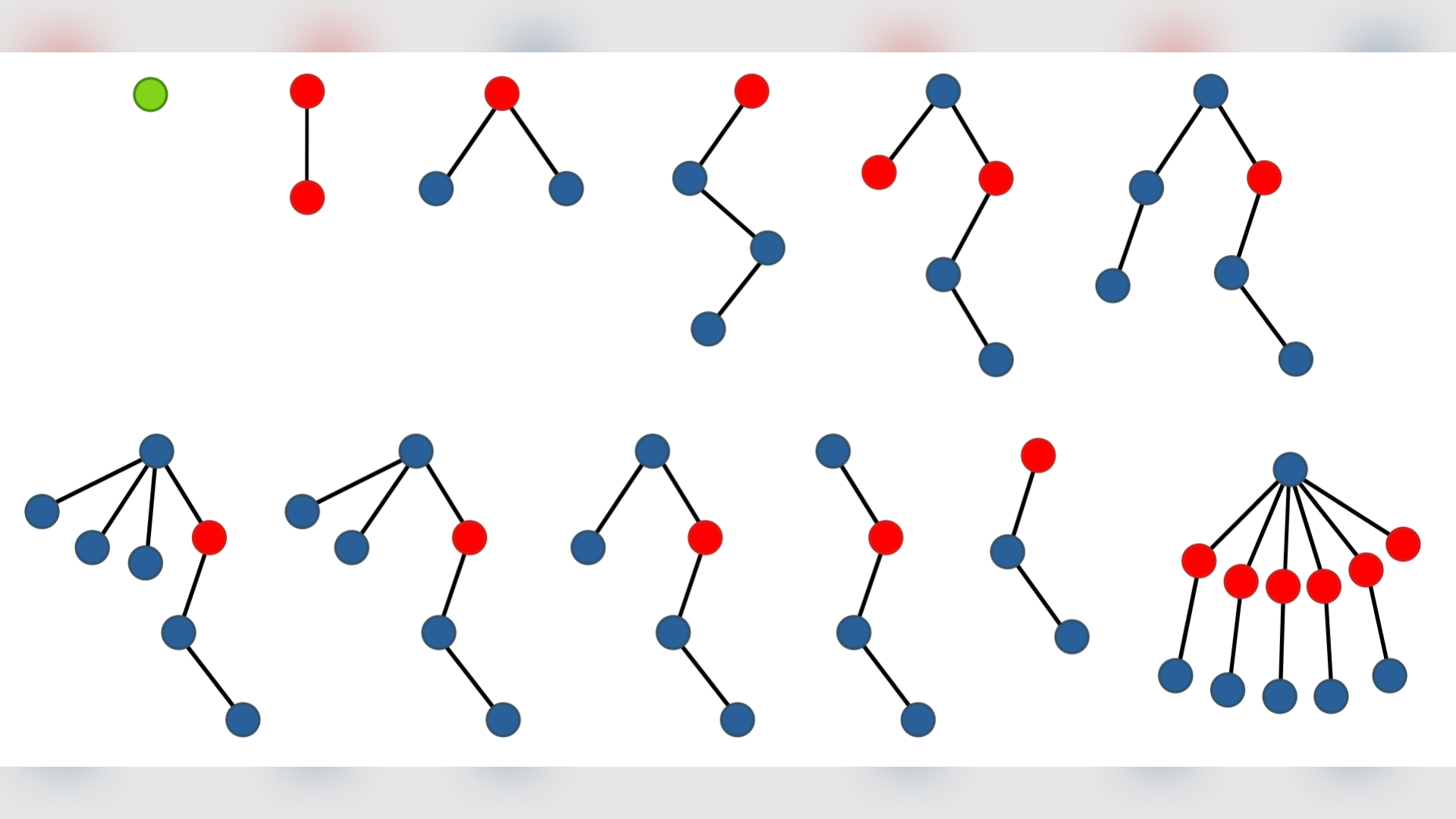
尽管格雷厄姆(Graham)的数字是为特定数学证明的最大数字之一,但此后数学家的数字甚至更大。 1998年逻辑学家哈维·弗里德曼俄亥俄州立大学提出了一个谜语询问需要给重复字母伸展的某些参数需要多长时间。虽然答案不是无限的,但绝对是巨大的。
Friedman得出的数字是通过使用称为Ackerman函数的东西创建越来越大的两二塔来计算的。为了给人一种规模的感觉,第四个Ackerman功能涉及将两个功率提高到65,536二。但是树(3)大大,大于大 - 如此之大,以至于它使Graham的数字看起来像是最微小的灰尘。
弗里德曼在他的论文中写道:“这些较高水平的巨大模糊,一个人无法从另一个人那里感觉到一个层次。”
编者注:本文最初于2013年发表,并于2023年11月17日更新,以注意有关可观察到的宇宙中最大的原子和宇宙学常数的新信息。在发现了新的最大质量数字之后,该文章在2024年10月再次更新。