做了一个团队数学家只是朝回答160年历史的数百万美元的数学问题迈出了一大步?
或许。机组人员确实解决了一个称为数字理论的领域中的许多其他较小的问题。这样一来,他们重新开放了一条旧的途径,最终可能会导致对旧问题的答案:是Riemann假设正确的?
雷曼假设是一种基本的数学猜想,对其余数学具有巨大的影响。它构成了许多其他数学思想的基础 - 但没人知道它是否为真。它的有效性已成为最著名的公开问题在数学中。这是七个”千年问题“在2000年布置,并承诺谁解决了他们将赢得100万美元。 (此后仅解决了其中一个问题。)[5认真令人难以置信的数学事实这是给出的
这个想法从何而来?
早在1859年,一位名叫Bernhard Riemann的德国数学家提出了一个特别棘手的数学方程式的答案。他的假设是这样的:riemann zeta函数的每个非平凡零的实际部分是1/2。那很漂亮抽象数学语句,必须与可以将哪些数字放入特定的数学函数中,以使该函数等于零。但事实证明,关于您遇到的频率的问题,最重要的是素数当您朝着无限统计时。
稍后,我们将回到假设的细节。但是现在要知道的重要一件事是,如果Riemann假设是正确的,它将回答许多数学问题。
“在数量理论中,最终发生的事情通常是,如果您假设Riemann假设(是真的),那么您就可以证明各种其他结果,”俄亥俄州Oberlin College的一位理论家Lola Thompson不参与这项最新研究,他说。
她经常告诉现场科学,数字理论家首先会证明,如果Riemann假设是真的,则是真的。然后,他们将使用该证明作为一种垫脚石迈向更复杂的证据,这表明他们的最初结论是正确的,无论Riemann假设是否为真。
事实这个技巧她说,著作说服了许多数学家,黎曼假设必须是真实的。
但事实是没有人确定。
朝着证明的一小步?
那么,这个小型数学家团队似乎是如何使我们更加靠近解决方案的呢?
埃默里大学(Emory University)的众多理论家,新证明的合着者肯·奥诺(Ken Ono)说:“我们在论文中所做的事情是,我们重新审视了一个非常技术性的标准,该标准等同于Riemann假设……我们证明了其中的很大一部分。我们证明了这一标准的很大一部分。”
在这种情况下,“等同于Riemann假设的标准”是指数学上等同于Riemann假设的单独陈述。
乍一看,这两个陈述是如此连接,这并不明显。 (标准与所谓的“詹森多项式的双曲线”有关。)但是在1920年代,匈牙利数学家乔治·波利亚(GeorgePólya)证明,如果这个标准是真的,那么Riemann假设是真实的 - 反之亦然。这是证明假设的一条古老的建议,但在很大程度上被放弃了。
Ono和他的同事在5月21日在《杂志》上发表的一篇论文中自然科学院论文集(PNA)证明,在许多情况下,标准是正确的。
但是在数学中,许多人不足以算作证明。在某些情况下,他们不知道标准是对还是错。
奥诺说:“这就像打一百万个电球球。” “而且您知道所有数字,但最后20个数字。如果最后20个数字中的一个是错误的,那么您就输了。…它仍然可能崩溃。”
在所有情况下,研究人员都需要提出更高级的证明,以证明该标准都是正确的,从而证明了Riemann假设。 Ono说,目前尚不清楚这样的证据有多远。
那么,这篇论文有多大的交易?
就Riemann假设而言,很难说这有多大。很大程度上取决于接下来会发生什么。
汤普森说:“这个[标准]只是里曼假设的许多等效表述之一。”
换句话说,还有许多其他想法,例如这个标准,如果他们自己自己被证明了。
汤普森说:“因此,很难知道这是多少进展,因为一方面它在这个方向上取得了进展。但是,有很多等效的表述,也许这个方向不会产生Riemann假设。
如果证明沿着这条轨道出现,那么这可能意味着Ono和他的同事开发了一个重要的基础框架来解决Riemann假设。但是,如果它出现在其他地方,那么本文将变得不太重要。
尽管如此,数学家仍然留下了深刻的印象。
“尽管这与证明Riemann假设相去甚远,但这是一大步,”普林斯顿人数理论家Encrico Bombieri在5月23日的陪同下写道。PNAS文章。 “毫无疑问,本文将激发其他数量理论以及数学物理学领域的进一步基本工作。”
(Bombieri赢得了田野勋章- 数学上最负盛名的奖项 - 1974年,在很大程度上是与Riemann假设有关的工作。)
无论如何,Riemann假设是什么意思?
我保证我们会回到这一点。这再次是Riemann假设:Riemann Zeta函数的每个非平凡零的实际部分是1/2。
让我们根据汤普森(Thompson)和昂诺(Ono)解释它的方式将其分解。
首先,Riemann Zeta功能是什么?
在数学中,一个函数是不同数学数量之间的关系。一个简单的看起来可能是这样的:y = 2x。
Riemann Zeta函数遵循相同的基本原理。只有更复杂。这就是它的样子。
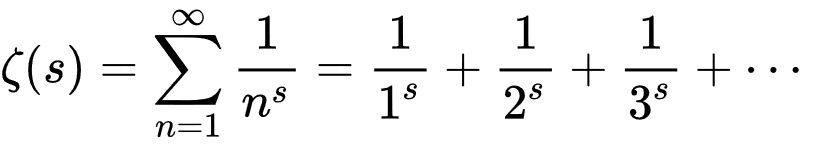
这是一个无限顺序,每个术语 - 前几个是1/1^s,1/2^s和1/3^s-添加到上一项中。这些椭圆形意味着该功能中的系列永远继续进行。
现在我们可以回答第二个问题:Riemann Zeta函数的零是什么?
这很容易。该函数的“零”是您可以为X放入任何数字,这会导致函数等于零。
下一个问题:其中一个零的“真实部分”是什么,它等于1/2是什么意思?
Riemann Zeta功能涉及数学家所说的”复杂数字。“一个复杂的数字看起来像这样:a+b*i。
在该方程式中,“ A”和“ B”代表任何实际数字。实际数字可以是从负3到零到4.9234的任何东西,pi,约10亿。但是还有另一种数字:假想的数字。当您取下负数的平方根时,会出现虚构数字,并且在各种数学环境中出现。 [关于PI的10个令人惊讶的事实这是给出的
最简单的假想数是-1的平方根,其写为“ i”。一个复杂的数字是一个实数(“ a”)加上另一个实数(“ b”)次i。复杂数字的“实际部分”是“ a”。
Riemann Zeta函数的一些零,即-10至0之间的负整数,不计入Reimann假设。这些被认为是“微不足道”的零,因为它们是实数,而不是复数。所有其他零是“非平凡”和复数。
Riemann假设指出,当Riemann Zeta函数交叉零(除-10和0之间的零以外)时,复数的实际部分必须等于1/2。
这个少的主张听起来可能不是很重要。但这是。而且我们可能只是更接近解决它的十几岁。
最初出版现场科学。