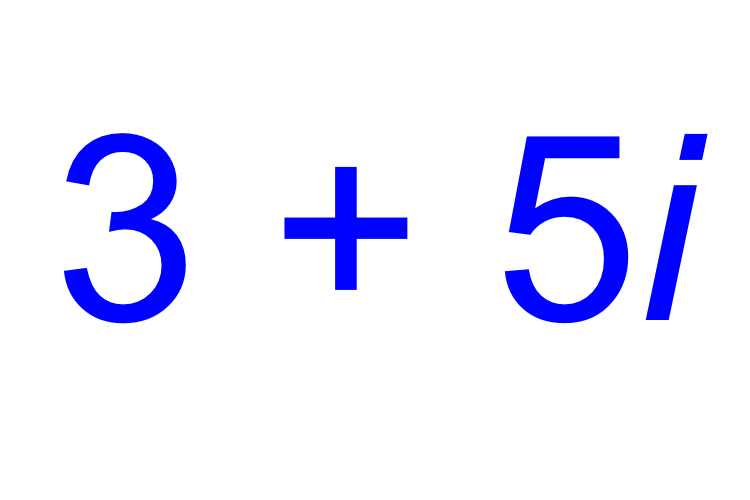
复数数字是由两个部分组成的数字 - 一个实际数字和一个想象的数字。复数是更复杂的数学的基础,例如代数。它们可以应用于现实生活的许多方面,尤其是在电子和电磁主义中。
复数的标准格式是和 + bi,首先具有实数,而虚构的数字持续。因为任何一部分都可以是0,从技术上讲任何部分真实数字或者假想的数字可以认为是一个复杂的数字。复杂并不意味着复杂;这意味着两种类型的数字结合在一起形成一个复杂的建筑,例如住房建筑群 - 一组建筑物融合在一起。
实数是可以在水平数字线上绘制的有形值,例如分数,整数或您可以想到的任何可计数数字。假想数是当您需要负数的平方根时使用的抽象概念。
添加和乘以复数
因为一个复杂的数字是二项式(具有两个术语的数值表达式),通常以与任何二项式相同的方式进行算术,通过结合类似项和简化。例如:
(3 + 2i) +(4-4i)
(3 + 4)= 7
(2i -4i)= -2i
结果就是7-2i。
对于乘法,您采用箔方法进行多项式乘法:乘以第一个,将外部乘以内部乘以内部,乘以最后一个,然后添加。例如:
(3-2i)(5 + 3i)=
(3)(5) +(3)(3i) +(-2i)(5)(5) +(-2i)(3i)=
15 + 9i + -10i + -6i2=
15 -i -6(-1)=
21- i
原因i2简化为(-1)是因为我是-1的平方根。
划分复数
但是,分裂变得更加复杂,需要使用缀合物。复杂的缀合物是一对具有不同符号的复数成对,例如(a + bi)和(a -b)。乘以复杂的偶联物会导致中间术语取消。例如:
(a + bi)(a -b)= a2-ABI + ABI-(BI)2
这简化为2- b2(我2)= a2- b2(-1)
最终结果是2+ b2
在划分复数时,请确定分母的偶联物,然后将分子和分母乘以结合物。例如,
(5 + 2i)÷(7 + 4i)
7 + 4i的共轭为7-4i。因此,将分子和分母乘以结合:
(5 + 2i)(7-4i)÷(7 + 4i)(7-4i)=
(35 + 14i - 20i - 8i2)÷(49-28i + 28i -16i2)=
(35-6i + 8)÷(49 + 16)=
(43-6i)÷65
复数的绝对值
一个数字的绝对值被认为是其与数字线上零的距离。由于复数数字包含假想数字,因此无法将它们绘制在实际数字行上。但是,它们可以从复数平面上的零来测量,该平面包括一个X轴(用于实际数字)和Y轴(对于假想数)。
复数的用途
复数可用于求解零的二次。二次配方解决AX2 + BX + C = 0对于x的值。如果公式在平方根中提供负,则可以使用复数来简化零。
复数用于电子和电磁作用。一个复杂的数字将两个实际数量汇总在一起,从而使数字更易于使用。例如,在电子设备中,电路元件的状态由电压(v)和电流(i)定义。电路元件也可以具有电容(C)和电感(L),该电路元素描述了电路抵抗V和I的变化的趋势。而不是通过V和I描述电路元件的状态,可以描述为Z = V + II。然后,可以使用复杂umbers的添加和乘法来表示电力定律。
如前所述,这也可以应用于电磁学。您可以在电场强度和磁场强度上被描述为电场强度和磁场强度,而是可以创建一个复杂的数字,其中电气和磁性组件是真实和虚构的数字。