三角学是数学的一个分支,研究了三角形的侧面和角度之间的关系。在整个几何形状中都发现了三角学,因为每个直侧形状都可以作为三角形的集合分解成。此外,三角学与数学的其他分支,特别是复数,无限序列,对数和计算具有惊人的复杂关系。
三角学一词是从三角形的希腊语单词中的16世纪拉丁衍生物(Trigōnon)和衡量(地铁)。尽管该领域在公元前三世纪出现在希腊,但一些最重要的贡献(例如正弦功能)来自公元五世纪的印度,因为古希腊的早期三角学作品已经丢失,但尚不知道印度学者是独立或在希腊人的影响之后开发的三角晶。根据维克多·卡茨(Victor Katz)的说法数学史(第三版)”(Pearson,2008),三角学主要源于希腊和印度天文学家的需求。
一个例子:帆船桅杆的高度
假设您需要知道帆船桅杆的高度,但无法爬上测量。如果桅杆垂直于甲板和桅杆的顶部,则将桅杆固定在甲板上,则桅杆,甲板和索具绳形成右三角形。如果我们知道绳索离桅杆有多远,以及绳索与甲板相遇的倾斜,那么确定桅杆的高度就是三角学。
为此,我们需要研究几种描述“倾斜”的方法。首先是坡,这是一个比较比较一条线垂直增加多少单位的比率(其上升)与水平增加多少单位相比跑步)。因此,将斜率计算为“上升”除以运行。假设我们将索具的索具距离为30英尺(9.1米),距桅杆的底部(运行)。通过将运行乘以坡度,我们将获得上升 - 桅杆高度。不幸的是,我们不知道斜坡。但是,我们可以找到角度索具绳,并用它找到坡度。角度是一个完整圆的一部分,定义为具有360度。这很容易用量角器测量。让我们假设索具绳和甲板之间的角度为一个圆的71/360或71度。
我们想要坡度,但我们只有角度。我们需要的是与两者相关的关系。这种关系被称为“切线函数,写为tan(x)。一个角度的切线给出了斜率。对于我们的演示,方程为:tan(71°)= 2.90。
这意味着我们的索具绳的坡度为2.90。由于索具距离桅杆的底部30英尺,因此桅杆必须为2.90×30英尺或87英尺。 (它在公制系统中的工作相同:2.90 x 9.1米= 26.4米。)
正弦,余弦和切线
根据对右三角形的各个侧长和角度的了解,还有另外两个三角函数可能更有用:“正弦函数”以罪(x)和“余弦函数为cos(x)。在解释这些功能之前,需要一些其他术语。触摸的侧面和角度被描述为邻近的。每一侧都有两个相邻的角度。不触摸的侧面和角度被描述为对面的。对于右三角形,与直角相反的一侧称为斜边(来自希腊语“伸展下”)。剩下的两个侧被称为腿。
通常,我们(如上所述)以除正确角度以外的角度感兴趣。我们所谓的“上升”在上面的示例中被视为与感兴趣角度相反的腿的长度。同样,“运行”也被视为相邻腿的长度。当应用到角度度量时,三个三角函数会产生侧长比的各种组合。
换句话说:
- 角度的切线a =相对侧的长度除以相邻侧的长度
- 角的正弦a =相对侧的长度除以斜边的长度
- 角度a =相邻侧的长度除以斜边的长度
从我们之前的船上示例中,可以从其图中确定一个角度与切线之间的关系,如下所示。还包括正弦和余弦的图。
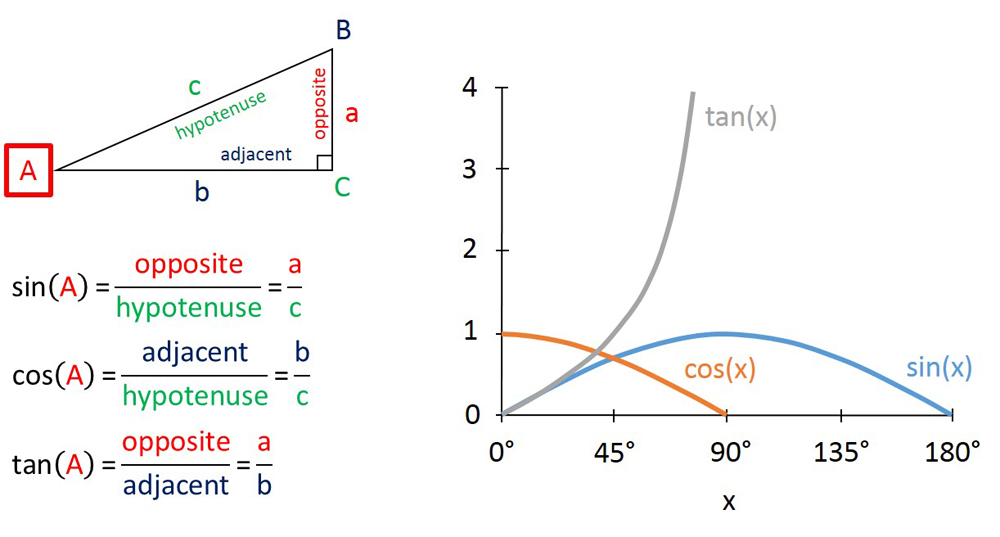
值得一提的是,尽管本文的范围超出了本文的范围,但这些功能通过称为复杂的方程式相互关联身份,始终是真实的方程式。
每个三角函数还具有一个逆,可用于从边比的角度找到一个角度。 SIN(X),COS(X)和TAN(X)的倒置分别为Arcsin(X),Arccos(X)和Arctan(X)。
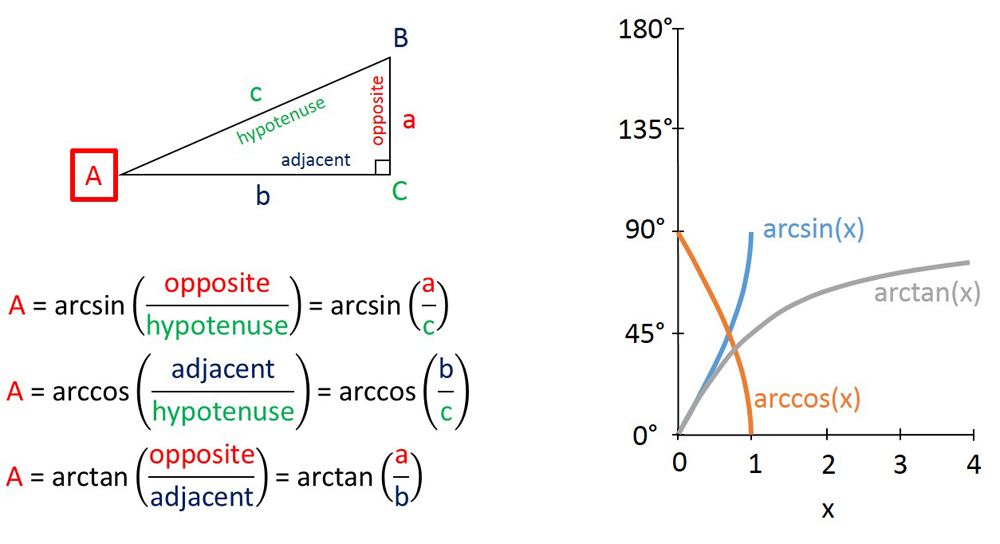
除右三角形以外的其他形状
三角学不仅限于正确的三角形。它可以与所有三角形和所有形状的直边一起使用,这些形状被视为三角形的集合。对于任何三角形,在六个侧面和角度的度量中,如果至少知道三个,则通常可以确定其他三个。在三个已知侧面和角度的六个配置中,只有两种配置不能用于确定三角形的所有内容:三个已知角度(AAA),以及已知角度相邻的已知角度(已知侧面)(屁股)。使用以下工具确定未知的侧面长度和角度:
- 这罪法,这说明,如果已知三个相对角/侧对之一的两个度量,则可以仅根据一个已知的确定:sin(a)/a = sin(b)/b = sin(c)/c
- 这余弦定律,这说明可以从两个已知的侧面和它们之间的角度找到一个未知的侧面。本质上是毕达哥拉斯定理,其角度的校正因子不是90度:C2 = a2 + b2 - 2ab cos(c)
- 一个事实是三角形必须加起来180度:A + B + C = 180°
三角学的历史
三角学遵循类似的路径代数:它是在古代中东开发的,通过贸易和移民迁至希腊,印度,中世纪阿拉伯和欧洲(因此,殖民主义使它成为当今大多数人的版本)。三角发现的时间表使印度和阿拉伯在跨文化边界的知识传递之后继续在研究中脱颖而出,这一事实变得复杂。例如,Madhava的1400发现无限系列正弦通过艾萨克·牛顿(Isaac Newton)在1670年的独立发现而不知所措。由于这些并发症,我们将仅关注正弦,余弦和切线的发现和通过。
从中东开始,新巴比尼的七世纪BC学者确定了一种计算十二生肖固定恒星的上升时间的技术。在黎明之前,一个不同的固定恒星大约需要10天,而12个十二生则迹象中的每个恒星都有三个固定的恒星。 10×12×3 = 360。数字360足够接近一年中的365.24天,但可以使用更方便。在其他古代文明的文本中发现了几乎相同的分歧,例如埃及和印度河谷。根据UTA Merzbach的说法数学史”(Wiley,2011年),希腊学者炒作对这种巴比伦技术的适应大约150 bc,这可能是NICEA(190至120 bc)的灵感,开始将圆切成360度的趋势,即使用几何形状,不再使用360度。Th一个圆)。亚历山大的托勒密(公元90年至168年),在他的公元148年“Almagest”,通过确定增量为0.5度的三角值通过确定河马的工作(720Th一个圆)从0到180度。
正弦功能的最古老记录来自Aryabhata(476至550)的第五世纪印度。第1.12节Aryabhatiya”(499),而不是以程度表示角度,而是包含罪恶的顺序差异列表二十四分之一角(增量为3.75度)。这是几个世纪以来大部分三角学的发射点。
继承三角学的下一批伟大的学者是伊斯兰的黄金时代。 Abbasid Caliphate的第七位哈里发和巴格达智慧之家的创造者Al-Ma'mun(813至833)赞助了托勒密的“ Almagest”和Aryabhata的“ Aryabhatiya”的翻译。不久,al-khwarism(780至850)在“Zījal-Sindhind”(820)中产生了准确的正弦和余弦表。正是通过这项工作,三角学的知识首先出现在欧洲。根据Gerald Toomer的说法科学传记词典7,”虽然原始的阿拉伯版本丢失了,但它的编辑大约为1000。Al-MajritiAl-Andalus(现代西班牙),他们可能添加了切线表巴斯的阿德拉德(在南英格兰)将其翻译成拉丁文,于1126年将其翻译成拉丁文。
其他资源