拓扑是数学的一个分支,它描述了数学空间,尤其是源于空间形状的属性。许多形状拓扑师都非常奇怪,以至于几乎所有日常物品(例如碗,宠物和树木)构成了少数群体。 “拓扑”一词源自希腊语的地方(拓扑)和研究(- 学)。
拓扑是在多个研究领域的指导中很重要的:
- 理论物理学(特别是量子力学例如量子场理论和弦理论)
- 宇宙学(用于确定宇宙的形状)
- 生物学(用于DNA的缠结并预测器官和其他身体部位的生长)
- 计算机科学(用于确定数据集的大规模结构)
- 机器人技术(在机器人臂的运动基础上根据空间的形状进行了多个维度等于臂接头数的形状)
连续变形
拓扑学家研究形状的特性,尤其是在形状扭曲,拉伸或变形后保留的拓扑特性。此允许更改的列表在数学概念下都被称为连续变形,这大致意味着“伸展,但不撕裂或合并”。例如,可以将一个圆圈拉到椭圆形或诸如手印轮廓之类的复合物中。撕裂和合并是因为所谓的不连续,所以他们不允许。
两个可以伸展到同一形状的物体被描述为同型,来自拉丁语希腊语的“类似”(同源)和希腊语“形式,形状或图形”(Morphe)。通过这个镜头,几乎所有日常物体都是同质的,带有球(一个球)或各种圆环(甜甜圈)。
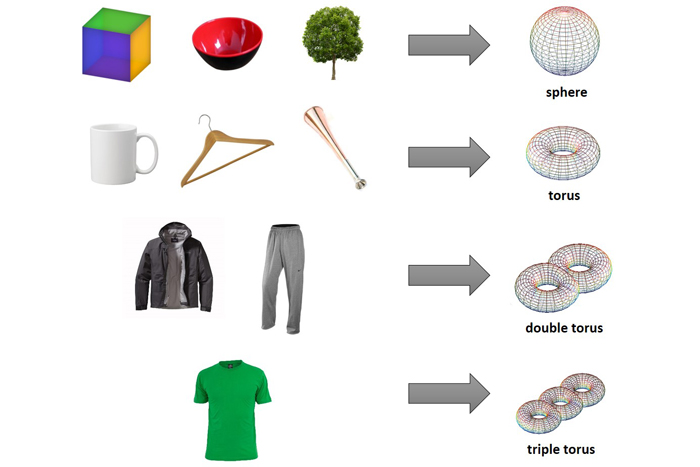
拓扑的某些分支使对象在伸展时可以通过自身;其他人没有。考虑表面能通过自身,重要的是不要无限紧绷,因为这也增加了不连续性。通常,当表面重新向后翻倍时,例如试图将球体向外旋转时(这很困难,但可能)。
欧拉的特征
在连续变形下不变的属性的一个示例是对象的欧拉的特征,以18岁的Leonhard Euler的名字命名Th- 世纪德国数学家。
为了展示物体的欧拉特征,首先,我们取下一个球(或带有球体的物体同构物体,例如人头),然后用多边形在表面上瓷砖。然后,我们计算面部(侧面),边缘(两个侧面相遇的地方)和顶点(三个或三个侧面相遇的地方)的数量。现在,添加面(F)和顶点(V)的数量,并减去边缘(E):F + V - E的数量。答案总是一样:两个。由于五个柏拉图固体(由一种常规多边形制成的3-D形状都是同态的,因此它们也具有两个欧拉的特征。
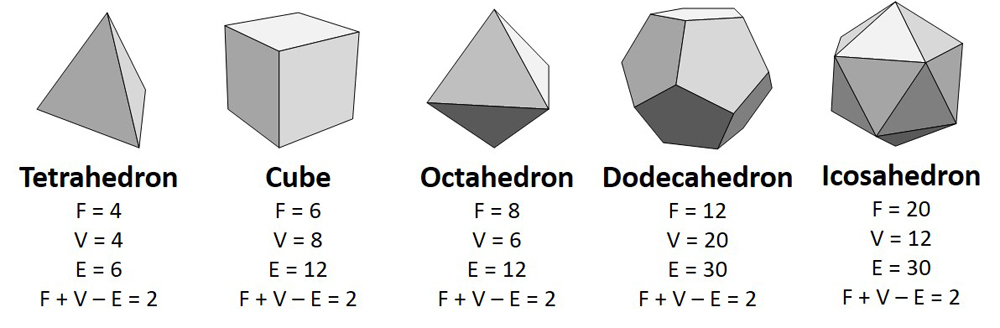
如果我们考虑添加边缘或顶点的含义,那么我们就可以理解为什么欧拉的特征得到保存。在两个顶点之间添加一个边缘将一张脸分成两面:边缘增加一个,脸部增加一个,顶点保持不变。同样,沿边缘添加一个顶点将边缘分为两个:边缘增加一个,顶点增加一个,并且面保持相同。
现在,曲线的表面,count f,v和e的表面,您将获得零的特征。这是一个例子:
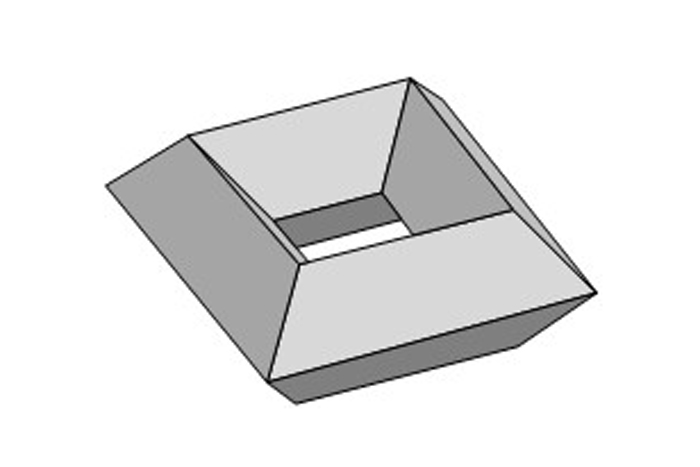
用双带,欧拉的特征为负两个。对于三重圆环,负四。每个额外的孔可将欧拉的特性减少两个。
不可定向的表面
到目前为止,我们谈论的所有形状的一件事是,据说它们是可调节的。这意味着在外表面上行走的错误将始终留在外面。内部也是如此。也有不稳定表面,这意味着表面上流浪的错误最终都可以在两侧。最著名的例子是Mobius Strip(其具有零的EULER特性,EC = 0)。

尽管“莫比乌斯脱带的双方”之类的语言对于介绍该概念很有用,但它与拓扑学家的思想背道而驰,他说任何表面都是2-d,而居住的人也是如此。通过这种镜头,想到生活在表面本身中的2D错误更有用。对于可定向的表面,有右手错误和左手错误,但是对于不可定向的表面,右手和左手的错误是无法区分的。这强调了Mobius带代表一个空间,我们对源于该空间形状的特性感兴趣。
基本多边形
以这种表面为2-D的观点,可以方便地表示拓扑空间基本多边形。要将基本多边形的2-D表面变成3-D对象,请拉伸表面,以便相应的侧面与箭头指示的方向相连。可以看出,连接平行的边是一个圆柱体(EC = 0),并且连接反行线使Mobius带(EC = 0)。
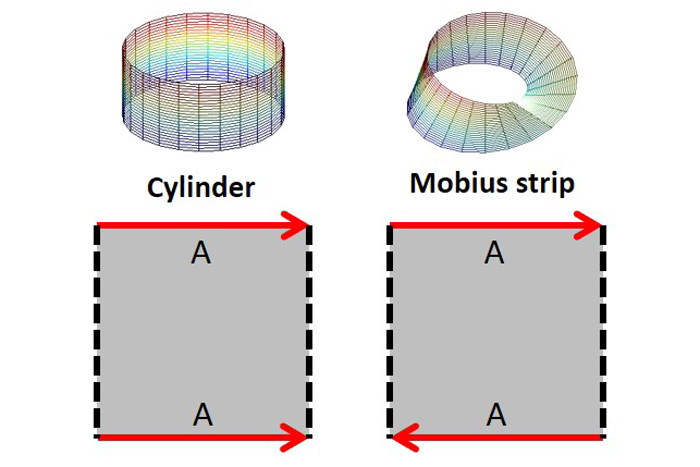
一个基本多边形的箭头和箭头边界的二维错误被运输到另一个边界,与箭头方向相比,以相同的方式定向。该错误是否保持相同或翻转表示表面是可定向还是不可定向。不允许二维错误越过虚线边界。
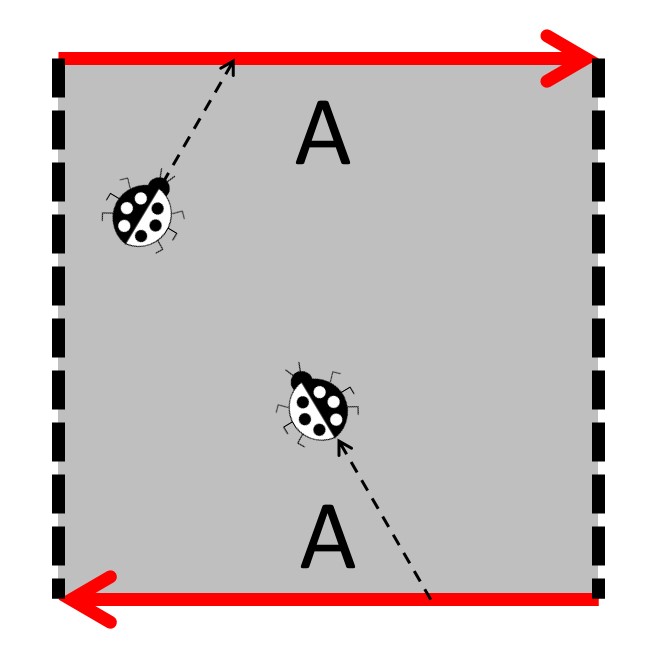
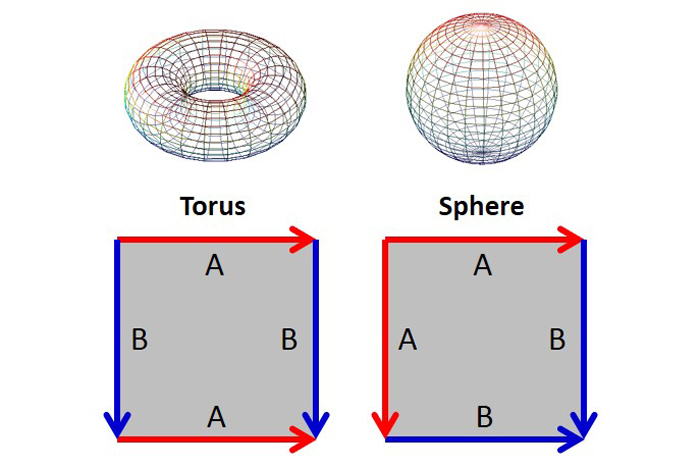
我们谈论的最初形状也具有基本的多边形。要制作圆环,首先制作一个圆柱体,然后伸展圆柱的末端,直到它们相遇为止。要制作一个球体,请从角落到角落折叠纸张以制作一个三角形的信封,然后将其充气直至球形。
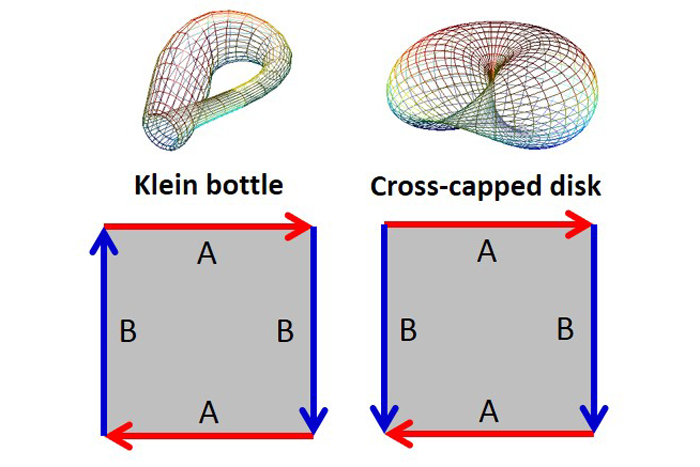
可以通过两种不同的方式组合莫比乌斯带的虚线边缘,以产生两个不可方向的表面:可以将klein瓶(EC = 0)视为莫比乌斯带和圆柱之间的交叉,并且可以将一个交叉式磁盘(EC = 1)视为两个Mobius Strips之间的交叉。与Mobius带一样,如果有第三个维度可以包含这张地图,我们可以从空间的整体“形状”中获得一些视角。两种结构都要求允许表面通过自身。二维错误不会注意到这样的交叉点;只有在二维空间中走某些路径后,世界才“翻转”。
拓扑中的著名问题
拓扑已经存在了几个世纪,但已经有一个有自己的故事的问题和子领域的悠久历史。
- 科尼格斯伯格的七个桥梁:经常被认为是拓扑中的第一个问题。古老的普鲁士小镇科尼格斯伯格(Königsberg)曾经有七座桥梁,其人民想知道是否可以走一条只越过每座桥的小路。 1735年,欧拉(Euler)证明这样的道路是不可能的。
- 手掌和指纹的图案:指纹都具有常见的特征,例如循环和triradii(三线汇聚在一起)。 1965年,英国医学遗传学家莱昂内尔·彭罗斯(Lionel Penrose)指出,指纹和棕榈印花遵守普遍的规则:每个人出生的五个手指的人总是比循环多四个。
- 毛茸茸的球定理:对于被头发覆盖的球(或球形),不可能将所有头发梳理。必须至少有一个地方伸直头发。
- 球体势头:对于允许通过自身的球形表面,是否有可能在不捏任何区域无限紧身的情况下将球体完全转动?这很棘手,但是是的。
- 结理论:结理论是拓扑内的一门学科,只涉及无法通过自己或他人的托里(复数)。结理论的主要重点是确定两个外观的结是否是同态。
- 庞加莱的猜想:在本文中,我们只检查了2D空间,但是还有一些以奇怪方式连接的3D空间。这庞加莱的猜想,最初于1904年首次摆姿势,是关于这些3D空间的,指出“每个简单连接的,封闭的3个manifold都是同型3-Sphere。”近一个世纪后,2000年粘土数学学院选择了七个未解决的“千年奖”问题,其中100万美元将被授予任何找到解决方案的人。庞加莱的猜想是第一个要解决的问题。俄罗斯数学家格里戈里·佩雷尔曼(Grigori Perelman)于2002年找到了解决方案,他拒绝了千年现金奖和田野奖章(许多人认为等同于诺贝尔的数学奖)。
其他资源