ในที่สุดนักคณิตศาสตร์ก็สามารถแก้ปัญหาโซฟาเคลื่อนที่แบบโบราณได้ในที่สุด

นักคณิตศาสตร์มักจะไม่ใช่ประเด็นแรกในวันย้าย และจริงๆ แล้วทำไมพวกเขาถึงควรเป็นเช่นนั้น? เป็นเวลาเกือบ 60 ปีแล้วที่พวกเขาไม่สามารถบอกคุณได้ว่าโซฟาสามที่นั่งสุดเก๋ตัวใหม่ของคุณจะเข้ามาอยู่ในอพาร์ตเมนต์ของคุณหรือไม่

Jineon Baek อาจจะเปลี่ยนใจเราในเรื่องนั้น ผู้ชื่นชอบการผสมผสานและเรขาคณิตจากมหาวิทยาลัยยอนเซในประเทศเกาหลีเพิ่งลดลงหลักฐาน 100 หน้าในปัญหานี้ การแก้ปัญหาเร่งด่วนที่สุดประการหนึ่งของจักรวาลเพื่อให้เราทุกคนสามารถเลือกเฟอร์นิเจอร์ได้ดีขึ้นก่อนที่จะติดอยู่บนปล่องบันไดชั้นสาม

ในปี 1966ลีโอ โมเซอร์ นักคณิตศาสตร์ชาวออสเตรีย-แคนาดา ได้สร้างปัญหาที่คุกคามมนุษยชาตินับตั้งแต่ที่เหนื่อยล้าออสเตรโลพิทิคัสตอนแรกยืนอยู่ในถ้ำอันไกลโพ้นพร้อมกับซากละมั่งที่ดูสบายตัวซึ่งจะไม่ขยับเขยื่อนอีกต่อไป

ภายนอกดูเหมือนตรงไปตรงมา วัตถุสองมิติที่ใหญ่ที่สุดที่สามารถหมุนรอบมุมรูปตัว L ได้สำเร็จคืออะไร

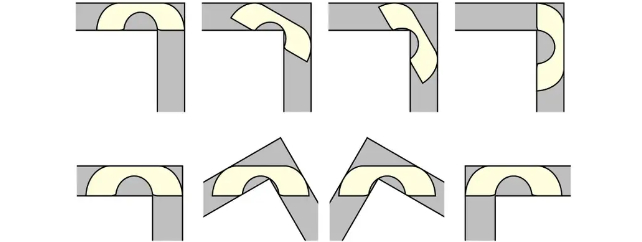
สำหรับทางเดินที่มีพื้นที่ 1 ยูนิต เก้าอี้ที่มีขนาด 1 ตร.ม. ก็เหมือนกับการเดินเล่นในสวนสาธารณะ ในทางกลับกัน หน่วยสองสี่เหลี่ยมจัตุรัสที่สมบูรณ์แบบจะติดค้างอย่างเห็นได้ชัด ลืมอะไรไปได้เลย ตอนนี้มันอาศัยอยู่บนทางเดินแล้ว

แต่จะเป็นอย่างไรหากสิ่งของของ IKEA มีเอกลักษณ์เฉพาะตัวที่มีชื่อเหมือนตัวละครใน Lord of the Rings และมีรูปร่างเหมือนเครื่องรับโทรศัพท์รุ่นเก่าล่ะ?

แค่สองปี.หลังจากที่โมเซอร์โยนถุงมือลง นักคณิตศาสตร์ชาวอังกฤษ จอห์น แฮมเมอร์สลีย์ก็พบโซฟาที่ประกอบด้วยครึ่งวงกลมที่ผ่าออก คั่นด้วยสี่เหลี่ยมจัตุรัสโดยเอาส่วนที่กัดออกครึ่งวงกลมออก (โดยที่เพื่อนสามคนอาจแตะเข่าอย่างงุ่มง่ามขณะที่พวกเขาพูดคณิตศาสตร์) อาจเป็น 2.2074 หน่วยในพื้นที่และยังคงเป็นเพียง ทำให้มันอยู่ตรงหัวมุม

แฮมเมอร์สลี่ย์ก็ตั้งเป้าเช่นกันขีดจำกัดบนสำหรับการออกแบบ – ไม่มีอะไรใหญ่กว่า 2.8284 ที่จะผ่านไปได้

เกือบหนึ่งในสี่ของศตวรรษผ่านไปก่อนที่นักวิชาการจากมหาวิทยาลัย Rutgers ชื่อ Joseph Gerver ได้เสนอแนะให้มีการออกแบบใหม่อันละเอียดอ่อนบนโซฟาของ Hammersly โดยปัดขอบบางส่วนออกด้วยส่วนโค้งพิเศษ และค้นหารูปทรงที่บวกเศษส่วนเข้ากับขีดจำกัดล่างก่อนหน้านี้เพื่ออ้างว่าขนาดโซฟาสูงสุดคือเศษส่วนมากกว่า 2.2195 ยูนิต-

Gerver ประสบความสำเร็จในการแสดงโซลูชันของเขาให้เหมาะสมที่สุดในท้องถิ่น โดยกำหนดขอบเขตล่างใหม่สำหรับพื้นที่สูงสุด กล่าวอีกนัยหนึ่ง วิธีแก้ปัญหาของเขาดีที่สุดภายใต้เงื่อนไขที่จำกัดซึ่งกำหนดโดยรูปร่างนั้น

หากไม่มีสูตรสากลสำหรับรูปทรงโซฟาที่อธิบายขนาดเฟอร์นิเจอร์ที่เป็นไปได้ทั้งหมด ก็เป็นเรื่องยากที่จะพิสูจน์ว่าโซฟาที่มีขนาดใหญ่กว่าเล็กน้อยและมีเส้นโค้งที่แตกต่างกันเล็กน้อยอาจไม่สามารถทำได้

ในปี 2561Yoav Kallus นักคณิตศาสตร์จากสถาบันซานตาเฟ่ และ Dan Romik จากมหาวิทยาลัยแคลิฟอร์เนีย Davis ใช้ระบบคอมพิวเตอร์ช่วยเพื่อแสดงโซฟาที่อาจสูงถึง 2.37 ยูนิต

สำหรับการพิสูจน์ครั้งล่าสุดนี้ Baek ได้ใช้เวทมนตร์ทางคณิตศาสตร์เล็กน้อยที่เรียกว่า aฟังก์ชั่นการฉีดเพื่อจัดวางรูปทรงโซฟาของ Gerver ที่ประสบความสำเร็จล็อคคุณสมบัติที่สำคัญก่อนที่จะขยายผ่านมิติที่ใหญ่ขึ้นเพื่อพิสูจน์ครั้งแล้วครั้งเล่าว่าโซฟาที่มีลักษณะคล้าย Gerver จะมีขนาดใหญ่เพียงใด

แน่นอนว่า 2.2195 ยูนิตคือราชาแห่งโซฟาสำหรับทางเดินกว้าง 1 ยูนิตและมุมรูปตัว L ดังที่ Gerver เสนอในปี 1992

แม้ว่าจะยังไม่ได้รับการตรวจสอบจากผู้ทรงคุณวุฒิ แต่วิธีแก้ปัญหาของ Baek ก็อาจเป็นคำตอบสุดท้ายเกี่ยวกับปัญหาโซฟา อย่างน้อยก็ในสภาพแวดล้อมนี้ หากคุณมีมุมที่สองให้หันไปในทิศทางตรงกันข้าม เราขอแนะนำรูปทรงที่เรียกว่าโซฟาสำหรับคนถนัดสองมือของ Romik

มีวางจำหน่ายแล้วที่ทางเดิน 13 ที่ IKEA ถัดจากโต๊ะในครัวของ Gimli

งานวิจัยนี้มีอยู่ในเซิร์ฟเวอร์ก่อนเผยแพร่อาร์เอ็กซ์-