ความงามเชิงตัวเลข

สมการทางคณิตศาสตร์ไม่ได้มีประโยชน์เพียงอย่างเดียว - หลายคนค่อนข้างสวยงาม และนักวิทยาศาสตร์หลายคนยอมรับว่าพวกเขามักจะชื่นชอบสูตรเฉพาะไม่เพียง แต่สำหรับการทำงานของพวกเขา แต่สำหรับรูปแบบของพวกเขาและความจริงที่เรียบง่ายและบทกวีที่พวกเขามี
ในขณะที่สมการที่มีชื่อเสียงบางอย่างเช่น E = Mc^2 ของ Albert Einstein แต่ Hog ของความรุ่งโรจน์สาธารณะส่วนใหญ่สูตรที่คุ้นเคยน้อยกว่ามีแชมป์เปี้ยนของพวกเขาในหมู่นักวิทยาศาสตร์ Livescience ถามนักฟิสิกส์นักดาราศาสตร์และนักคณิตศาสตร์สำหรับสมการที่พวกเขาชื่นชอบ นี่คือสิ่งที่เราพบ:
สัมพัทธภาพทั่วไป
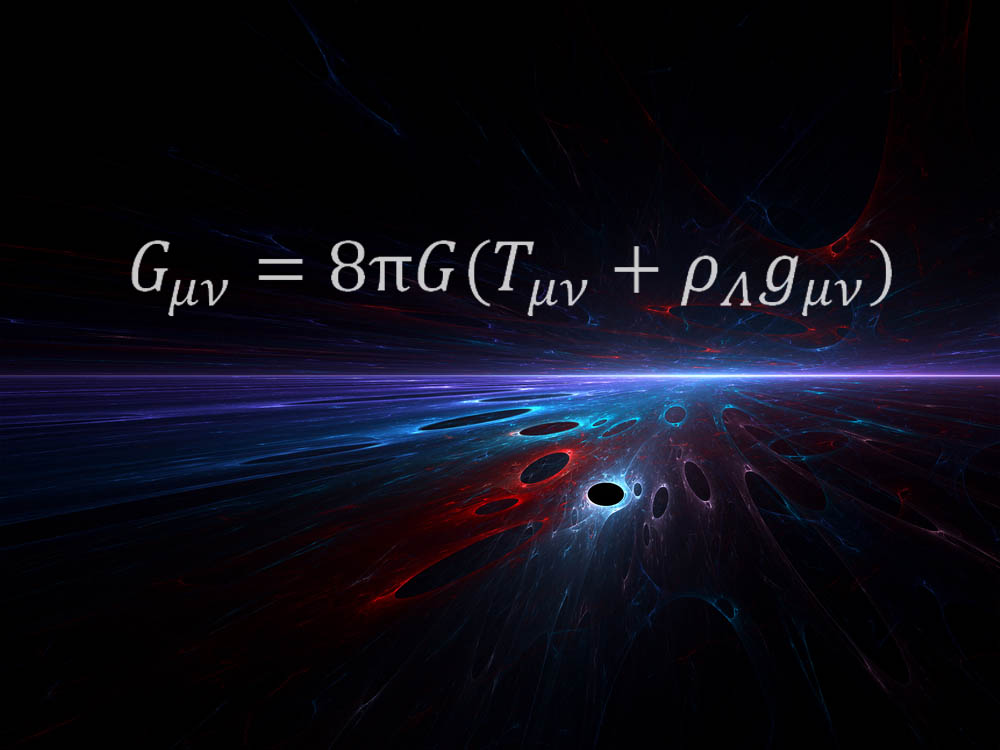
สมการข้างต้นถูกกำหนดโดยไอน์สไตน์เป็นส่วนหนึ่งของเขาที่ก้าวล้ำทฤษฎีสัมพัทธภาพทั่วไปในปี 1915 ทฤษฎีปฏิวัติวิธีที่นักวิทยาศาสตร์เข้าใจแรงโน้มถ่วงโดยการอธิบายถึงพลังในการแปรปรวนของผ้าของอวกาศและเวลา
“ มันยังคงน่าอัศจรรย์สำหรับฉันที่สมการทางคณิตศาสตร์อย่างหนึ่งสามารถอธิบายได้ว่าอวกาศเวลาเกี่ยวกับอะไร” สถาบันวิทยาศาสตร์กล้องโทรทรรศน์อวกาศมาริโอลิโอลิโอนักดาราศาสตร์ฟิสิกส์อวกาศ "อัจฉริยะที่แท้จริงของไอน์สไตน์ทั้งหมดเป็นตัวเป็นตนในสมการนี้" -Einstein Quiz: ทดสอบความรู้เกี่ยวกับอัจฉริยะของคุณ-
"ด้านขวามือของสมการนี้อธิบายถึงเนื้อหาพลังงานของจักรวาลของเรา (รวมถึง 'พลังงานมืด' ที่ขับเคลื่อนการเร่งความเร็วของจักรวาลในปัจจุบัน)" Livio อธิบาย "ด้านซ้ายมืออธิบายรูปทรงเรขาคณิตของอวกาศ-เวลาความเท่าเทียมกันสะท้อนถึงความจริงที่ว่าในสัมพัทธภาพทั่วไปของไอน์สไตน์มวลและพลังงานจะกำหนดรูปทรงเรขาคณิตและความโค้งซึ่งเป็นการรวมตัวกันของสิ่งที่เราเรียกว่าแรงโน้มถ่วง" -6 ข้อเท็จจริงแปลก ๆ เกี่ยวกับแรงโน้มถ่วง-
“ มันเป็นสมการที่สง่างามมาก” ไคล์แครนเมอร์นักฟิสิกส์ของมหาวิทยาลัยนิวยอร์กกล่าวเสริมว่าสมการเผยให้เห็นความสัมพันธ์ระหว่างเวลาอวกาศกับสสารและพลังงาน "สมการนี้จะบอกคุณว่าพวกเขาเกี่ยวข้องกันอย่างไร-การปรากฏตัวของอวกาศของดวงอาทิตย์วิปริตเพื่อให้โลกเคลื่อนที่ไปรอบ ๆ ในวงโคจร ฯลฯ มันยังบอกคุณว่าจักรวาลวิวัฒนาการมาอย่างไรตั้งแต่บิ๊กแบงและคาดการณ์ว่าควรมีหลุมดำ "
รุ่นมาตรฐาน

ทฤษฎีการปกครองของฟิสิกส์อีกประการหนึ่งรุ่นมาตรฐานอธิบายการรวบรวมอนุภาคพื้นฐานที่คิดว่าเป็นเอกภพของเรา
ทฤษฎีสามารถห่อหุ้มได้ในสมการหลักที่เรียกว่าแบบจำลองมาตรฐานลากรองจ์ (ตั้งชื่อตามนักคณิตศาสตร์และนักดาราศาสตร์ชาวฝรั่งเศสในศตวรรษที่ 18 โจเซฟหลุยส์ลากรองจ์) ซึ่งได้รับเลือกจากนักฟิสิกส์นักฟิสิกส์ Lance Dixon ของห้องปฏิบัติการเร่งความเร็วแห่งชาติ SLAC ในแคลิฟอร์เนีย
“ มันประสบความสำเร็จในการอธิบายอนุภาคและกองกำลังระดับประถมศึกษาทั้งหมดที่เราสังเกตเห็นในห้องปฏิบัติการจนถึงปัจจุบัน - ยกเว้นแรงโน้มถ่วง” Dixon บอกกับ Livescience "นั่นรวมถึงแน่นอนว่า Higgs (เช่น) Boson, PHI ในสูตรที่เพิ่งค้นพบเมื่อเร็ว ๆ นี้มีความสอดคล้องกันอย่างเต็มที่กับกลไกควอนตัมและสัมพัทธภาพพิเศษ"
อย่างไรก็ตามทฤษฎีโมเดลมาตรฐานยังไม่ได้รวมกันด้วยสัมพัทธภาพทั่วไปซึ่งเป็นเหตุผลว่าทำไมจึงไม่สามารถอธิบายแรงโน้มถ่วงได้ -Infographic: โมเดลมาตรฐานอธิบาย-
แคลคูลัส
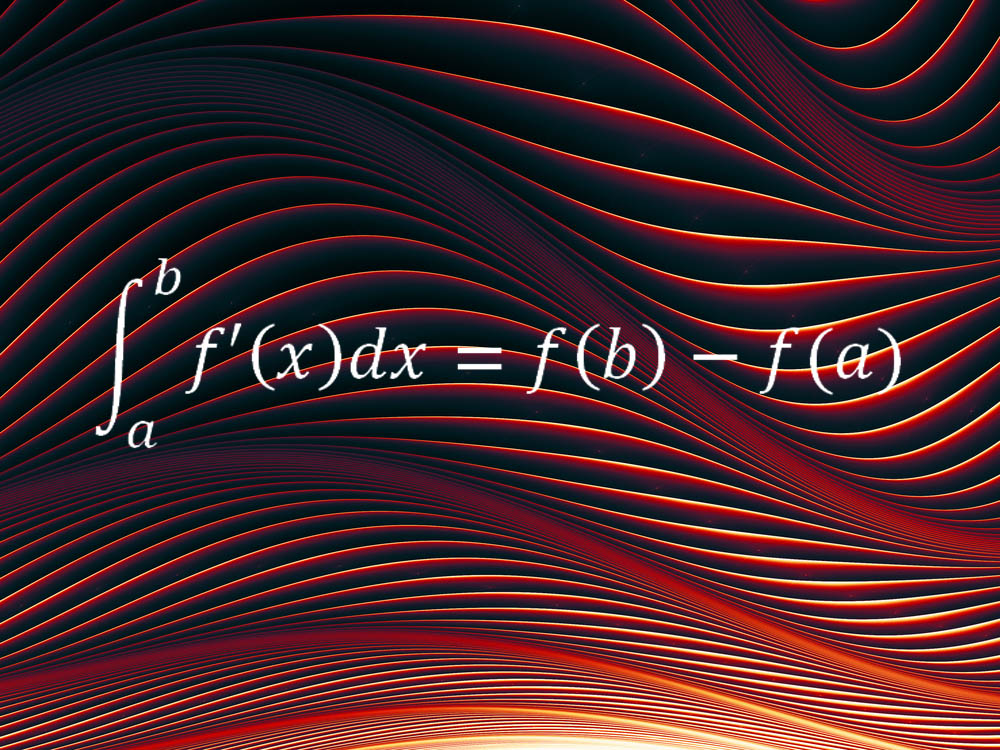
ในขณะที่สมการสองตัวแรกอธิบายแง่มุมเฉพาะของจักรวาลของเราสมการที่ชื่นชอบอีกอย่างสามารถนำไปใช้กับสถานการณ์ทุกรูปแบบ ทฤษฎีบทพื้นฐานของแคลคูลัสเป็นกระดูกสันหลังของวิธีการทางคณิตศาสตร์ที่เรียกว่าแคลคูลัสและเชื่อมโยงแนวคิดหลักสองประการแนวคิดของอินทิกรัลและแนวคิดของอนุพันธ์
"ในคำพูดง่ายๆ [มัน] บอกว่าการเปลี่ยนแปลงสุทธิของปริมาณที่ราบรื่นและต่อเนื่องเช่นระยะทางที่เดินทางในช่วงเวลาที่กำหนด (เช่นความแตกต่างในค่าของปริมาณในจุดสิ้นสุดของช่วงเวลา) เท่ากับค่ารวมของการเปลี่ยนแปลงของปริมาณการเลือก เป็นรายการโปรดของเธอ "ทฤษฎีบทพื้นฐานของแคลคูลัส (FTC) ช่วยให้เราสามารถกำหนดการเปลี่ยนแปลงสุทธิในช่วงเวลาตามอัตราการเปลี่ยนแปลงตลอดช่วงเวลา"
เมล็ดของแคลคูลัสเริ่มต้นขึ้นในสมัยโบราณ แต่ส่วนใหญ่ก็รวมตัวกันในศตวรรษที่ 17 โดยIsaac Newtonผู้ใช้แคลคูลัสเพื่ออธิบายการเคลื่อนไหวของดาวเคราะห์รอบดวงอาทิตย์
ทฤษฎีบทพีทาโกรัส

สมการ "Oldie But Goodie" เป็นทฤษฎีบทพีทาโกรัสที่มีชื่อเสียงซึ่งนักเรียนเรขาคณิตเริ่มต้นทุกคนเรียนรู้
สูตรนี้อธิบายถึงวิธีการสามเหลี่ยมที่มีมุมฉากสี่เหลี่ยมจัตุรัสของความยาวของ hypotenuse (ด้านที่ยาวที่สุดของสามเหลี่ยมด้านขวา) เท่ากับผลรวมของสี่เหลี่ยมของความยาวของอีกสองด้าน
"ความจริงทางคณิตศาสตร์ครั้งแรกที่ทำให้ฉันประหลาดใจคือทฤษฎีบทพีทาโกรัส" นักคณิตศาสตร์ Daina Taimina จากมหาวิทยาลัยคอร์เนลล์กล่าว "ตอนนั้นฉันเป็นเด็กและมันก็ดูน่าทึ่งมากที่มันใช้งานได้ในรูปทรงเรขาคณิตและใช้งานได้กับตัวเลข!" -5 ข้อเท็จจริงทางคณิตศาสตร์ที่เหลือเชื่ออย่างจริงจัง-
สมการของออยเลอร์
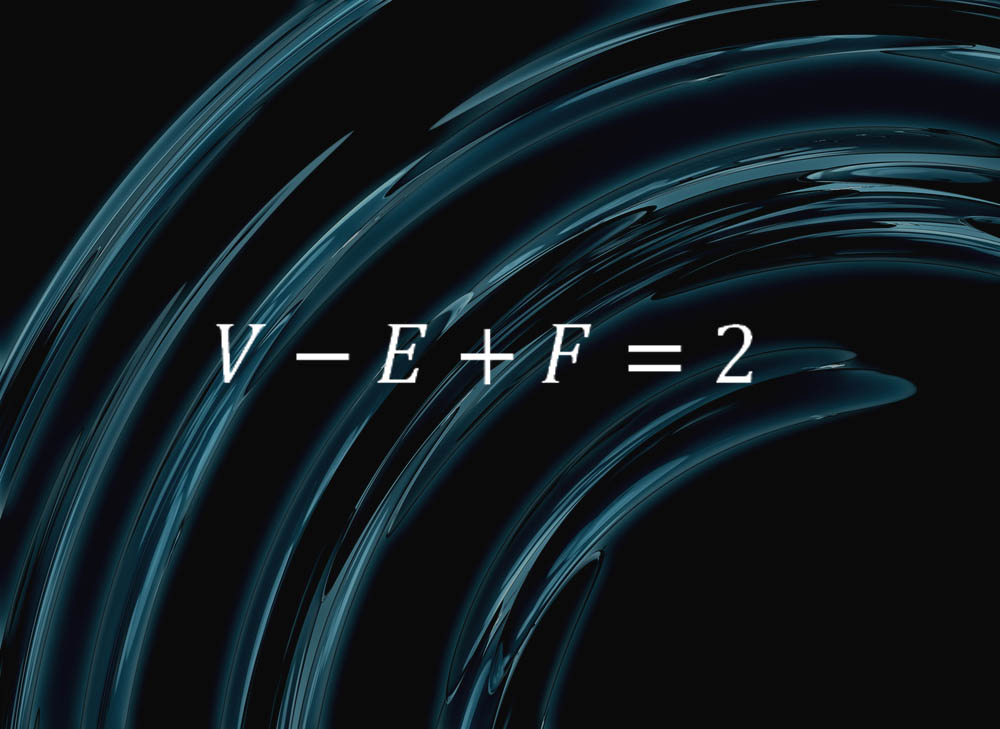
สูตรง่ายๆนี้ห่อหุ้มสิ่งที่บริสุทธิ์เกี่ยวกับธรรมชาติของทรงกลม:
“ มันบอกว่าถ้าคุณตัดพื้นผิวของทรงกลมขึ้นเป็นใบหน้าขอบและจุดยอดและปล่อยให้เป็นจำนวนใบหน้า e จำนวนของขอบและ v จำนวนจุดยอดคุณจะได้รับ V - E + F = 2 เสมอ” Colin Adams นักคณิตศาสตร์ที่วิทยาลัยวิลเลียมส์ในรัฐแมสซาชูเซตส์กล่าว
“ ยกตัวอย่างเช่นใช้จัตุรมุขประกอบด้วยสามเหลี่ยมสี่สามขอบหกขอบและสี่จุดยอด” อดัมส์อธิบาย "ถ้าคุณเป่าอย่างหนักเข้าไปใน tetrahedron ด้วยใบหน้าที่ยืดหยุ่นคุณสามารถปัดเศษเป็นทรงกลมดังนั้นในแง่นั้นทรงกลมสามารถตัดเป็นสี่ใบหน้าสี่ขอบและสี่จุดยอดและเราเห็นว่า V - E + F = 2
“ ความจริงที่ยอดเยี่ยมมาก! combinatorics ของจุดยอดขอบและใบหน้าคือการจับสิ่งที่พื้นฐานมากเกี่ยวกับรูปร่างของทรงกลม” อดัมส์กล่าว
สัมพัทธภาพพิเศษ
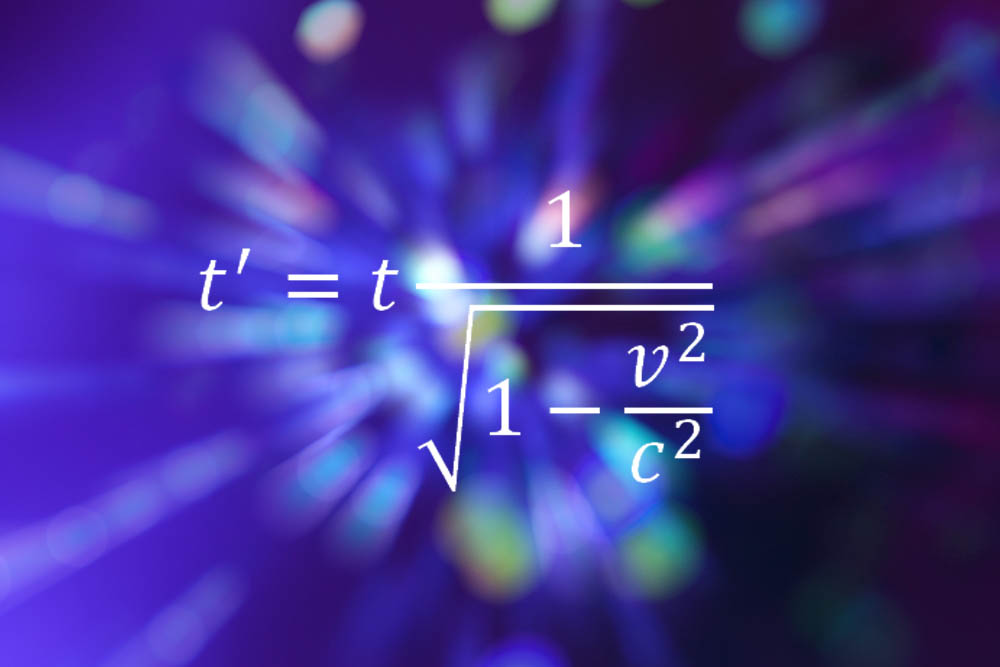
ไอน์สไตน์ทำรายการอีกครั้งด้วยสูตรของเขาสำหรับสัมพัทธภาพพิเศษซึ่งอธิบายว่าเวลาและพื้นที่ไม่ได้เป็นแนวคิดที่แน่นอน แต่เป็นความสัมพันธ์ขึ้นอยู่กับความเร็วของผู้สังเกตการณ์ สมการด้านบนแสดงให้เห็นว่าเวลาขยายตัวหรือช้าลงยิ่งคนเร็วขึ้นในทิศทางใด ๆ
“ ประเด็นก็คือมันง่ายมากจริงๆ” บิลเมอร์เรย์นักฟิสิกส์อนุภาคที่ห้องปฏิบัติการ CERN ในเจนีวากล่าว "ไม่มีอะไรที่นักเรียนระดับ A ไม่สามารถทำได้ไม่มีอนุพันธ์ที่ซับซ้อนและการติดตามพีชคณิต แต่สิ่งที่มันเป็นสิ่งที่รวบรวมคือวิธีใหม่ทั้งหมดในการมองโลกทัศนคติทั้งหมดต่อความเป็นจริงและความสัมพันธ์ของเรากับมันทันใดนั้นคุณจะไม่ได้อยู่ในโลก จับโดยใครก็ตามที่ต้องการ "
เมอร์เรย์กล่าวว่าเขาต้องการสมการสัมพัทธภาพพิเศษกับสูตรที่ซับซ้อนมากขึ้นในทฤษฎีของไอน์สไตน์ในภายหลัง “ ฉันไม่สามารถทำตามคณิตศาสตร์ของสัมพัทธภาพทั่วไปได้” เขากล่าว
1 = 0.999999999 ….

สมการง่าย ๆ นี้ซึ่งระบุว่าปริมาณ 0.999 ตามด้วยสายนินส์ที่ไม่มีที่สิ้นสุดนั้นเทียบเท่ากับหนึ่งเป็นที่ชื่นชอบของนักคณิตศาสตร์ Steven Strogatz แห่งมหาวิทยาลัยคอร์เนลล์
“ ฉันชอบความเรียบง่าย - ทุกคนเข้าใจในสิ่งที่พูด - แต่มันเป็นวิธีที่เร้าใจ” Strogatz กล่าว “ หลายคนไม่เชื่อว่ามันอาจเป็นจริงนอกจากนี้ยังมีความสมดุลอย่างสวยงามด้านซ้ายแสดงถึงจุดเริ่มต้นของคณิตศาสตร์ทางด้านขวาแสดงถึงความลึกลับของอินฟินิตี้”
ออยเลอร์ - สมการใบพัดและทฤษฎีบทของ Noether
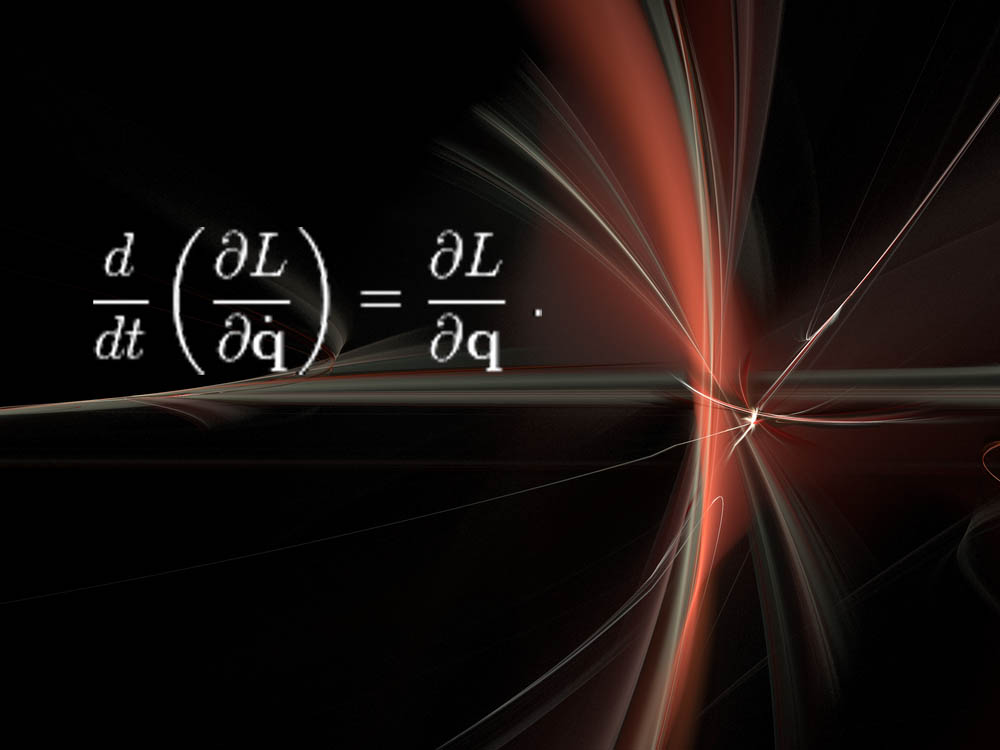
“ สิ่งเหล่านี้เป็นนามธรรม แต่ทรงพลังอย่างน่าอัศจรรย์” แครนเมอร์ของ Nyu กล่าว "สิ่งที่ยอดเยี่ยมคือวิธีคิดเกี่ยวกับฟิสิกส์นี้ได้รอดชีวิตจากการปฏิวัติครั้งใหญ่ในฟิสิกส์เช่นกลศาสตร์ควอนตัมสัมพัทธภาพ ฯลฯ "
ที่นี่ L ย่อมาจาก Lagrangian ซึ่งเป็นการวัดพลังงานในระบบทางกายภาพเช่นสปริงหรือคันโยกหรืออนุภาคพื้นฐาน “ การแก้สมการนี้จะบอกคุณว่าระบบจะพัฒนาไปตามกาลเวลาได้อย่างไร” แครนเมอร์กล่าว
สปินออฟของสมการลากรองจ์เรียกว่าทฤษฎีบทของ Noether หลังจากนักคณิตศาสตร์ชาวเยอรมันในศตวรรษที่ 20 “ ทฤษฎีบทนี้เป็นพื้นฐานของฟิสิกส์และบทบาทของความสมมาตร” แครนเมอร์กล่าว "อย่างไม่เป็นทางการทฤษฎีบทคือถ้าระบบของคุณมีสมมาตรจากนั้นก็มีกฎหมายการอนุรักษ์ที่สอดคล้องกัน ตัวอย่างเช่นความคิดที่ว่ากฎพื้นฐานของฟิสิกส์นั้นเหมือนกันในวันนี้ในวันพรุ่งนี้ (เวลาสมมาตร) หมายถึงพลังงานที่ได้รับการอนุรักษ์ ความคิดที่ว่ากฎของฟิสิกส์นั้นเหมือนกันกับที่อยู่ในอวกาศด้านนอกหมายความว่าโมเมนตัมได้รับการอนุรักษ์ Symmetry อาจเป็นแนวคิดการขับขี่ในฟิสิกส์พื้นฐานส่วนใหญ่เกิดจากการมีส่วนร่วมของ [Noether's] "
สมการ Callan-Symanzik
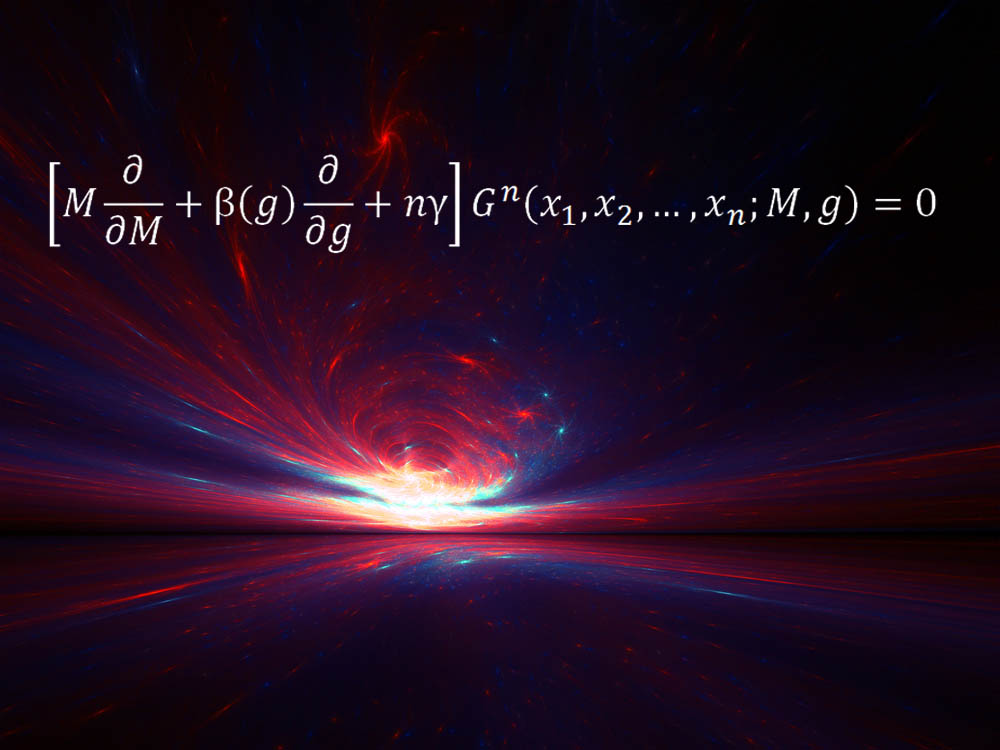
"สมการ Callan-Symanzik เป็นสมการหลักการแรกที่สำคัญจากปี 1970 สิ่งจำเป็นสำหรับการอธิบายว่าความคาดหวังที่ไร้เดียงสาจะล้มเหลวในกโลกควอนตัม"นักฟิสิกส์ทฤษฎี Matt Strassler จาก Rutgers University กล่าว
สมการมีการใช้งานมากมายรวมถึงการอนุญาตให้นักฟิสิกส์ประเมินมวลและขนาดของโปรตอนและนิวตรอนซึ่งประกอบขึ้นเป็นนิวเคลียสของอะตอม
ฟิสิกส์พื้นฐานบอกเราว่าแรงโน้มถ่วงและแรงไฟฟ้าระหว่างวัตถุสองชิ้นนั้นเป็นสัดส่วนกับการผกผันของระยะห่างระหว่างพวกเขากำลังสอง ในระดับที่เรียบง่ายนั้นเป็นจริงสำหรับแรงนิวเคลียร์ที่แข็งแกร่งที่ผูกโปรตอนและนิวตรอนเข้าด้วยกันเพื่อสร้างนิวเคลียสของอะตอมและผูกควาร์กเข้าด้วยกันเพื่อสร้างโปรตอนและนิวตรอน อย่างไรก็ตามความผันผวนของควอนตัมเล็ก ๆ สามารถเปลี่ยนการพึ่งพาของแรงเล็กน้อยในระยะทางซึ่งมีผลกระทบอย่างมากสำหรับแรงนิวเคลียร์ที่แข็งแกร่ง
“ มันป้องกันไม่ให้แรงนี้ลดลงในระยะทางไกลและทำให้มันกับดักควาร์กและรวมเข้าด้วยกันเพื่อสร้างโปรตอนและนิวตรอนในโลกของเรา” สแตสเลอร์กล่าว "สิ่งที่สมการ Callan-Symanzik มีความสัมพันธ์กับเอฟเฟกต์ที่น่าทึ่งและยากต่อการคำนวณสิ่งสำคัญเมื่อ [ระยะทาง] มีขนาดประมาณของโปรตอนไปจนถึงเอฟเฟกต์ที่ละเอียดอ่อนกว่า แต่ง่ายกว่าที่จะคำนวณได้
สมการพื้นผิวน้อยที่สุด
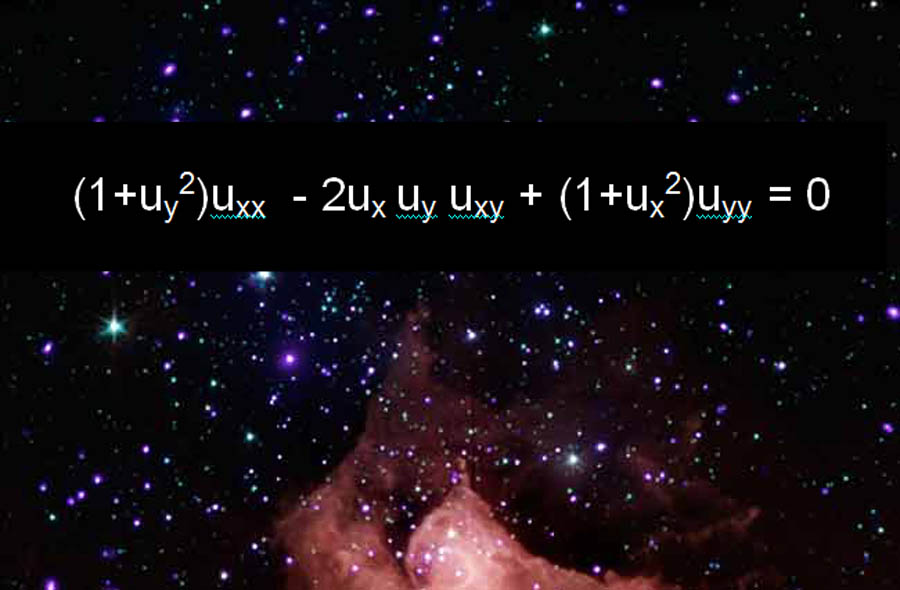
"สมการพื้นผิวที่น้อยที่สุดอย่างใดภาพยนตร์สบู่ที่สวยงามรูปแบบนั้นบนขอบเขตของสายไฟเมื่อคุณจุ่มลงในน้ำสบู่ "นักคณิตศาสตร์แฟรงค์มอร์แกนแห่งวิทยาลัยวิลเลียมส์กล่าว" ความจริงที่ว่าสมการนี้เป็น 'ไม่เชิงเส้น' ที่เกี่ยวข้องกับอำนาจและผลิตภัณฑ์ของอนุพันธ์คือคำใบ้ทางคณิตศาสตร์ที่น่าประหลาดใจสำหรับพฤติกรรมที่น่าประหลาดใจของภาพยนตร์สบู่ สิ่งนี้ตรงกันข้ามกับสมการเชิงเส้นเชิงเส้นบางส่วนที่คุ้นเคยเช่นสมการความร้อนสมการคลื่นและสมการSchrödingerของฟิสิกส์ควอนตัม "
เพิ่มเติมเกี่ยวกับคณิตศาสตร์




