รูปสามเหลี่ยมของ Pascal เป็นสามเหลี่ยมด้านเท่าที่ไม่มีที่สิ้นสุดของตัวเลขที่เป็นไปตามกฎของการเพิ่มตัวเลขสองตัวด้านบนเพื่อรับหมายเลขด้านล่าง สองด้านคือ“ ทั้งหมด 1” และเนื่องจากสามเหลี่ยมไม่มีที่สิ้นสุดจึงไม่มี“ ด้านล่าง”
มันมีชื่อสำหรับBlaise Pascalนักคณิตศาสตร์ชาวฝรั่งเศสในศตวรรษที่ 17 ที่ใช้สามเหลี่ยมในการศึกษาของเขาในทฤษฎีความน่าจะเป็น อย่างไรก็ตามมีการศึกษาทั่วโลกมาหลายพันปีโดยเฉพาะอย่างยิ่งในโบราณอินเดียและยุคกลางจีนและในระหว่างยุคทองของศาสนาอิสลามและยุคฟื้นฟูศิลปวิทยาซึ่งเริ่มขึ้นอิตาลีก่อนที่จะแพร่กระจายไปทั่วยุโรป
ง่ายเหมือนรูปแบบนี้มันมีการเชื่อมต่อที่น่าประหลาดใจตลอดหลายพื้นที่ของคณิตศาสตร์รวมถึงพีชคณิต, ทฤษฎีจำนวน, ความน่าจะเป็น, combinatorics (คณิตศาสตร์ของการกำหนดค่าที่นับได้) และเศษส่วน ในคอลัมน์ "ผู้เชี่ยวชาญ Voices" สำหรับวิทยาศาสตร์การแสดงสดปี 2013 Michael Rose นักคณิตศาสตร์ที่เรียนที่ University of Newcastle ได้อธิบายถึงหลาย ๆรูปแบบที่ซ่อนอยู่ในสามเหลี่ยมของ Pascal- ในบทความนี้เราจะเจาะลึกลงไปในคุณสมบัติที่พบในคณิตศาสตร์ที่สูงขึ้น
การรวมกัน
สามเหลี่ยมของ Pascal เกิดขึ้นตามธรรมชาติผ่านการศึกษาของ combinatorics ตัวอย่างเช่นลองนึกภาพการเลือกสามสีจากเครื่องหมายห้าสี ลำดับที่เลือกสีนั้นไม่สำคัญว่าจะเลือกใช้กับโปสเตอร์ แต่ใช้สำหรับการเลือกสีเดียวสำหรับอลิซบ๊อบและแครอล จำนวนการกำหนดค่าที่เป็นไปได้จะถูกแสดงและคำนวณดังนี้:
- สีเดียวสำหรับอลิซบ๊อบและแครอล: กรณีเช่นนี้ที่สั่งซื้อทำเรื่องเรียกว่ากการเปลี่ยนแปลง- สำหรับกรณีที่มีห้าตัวเลือกที่สามจะถูกเลือกและสั่งซื้อจำนวนการเรียงสับเปลี่ยนที่เป็นไปได้นี้จะแสดงเป็น 5p3 และคำนวณเป็น 5!/(5-3)! ผู้ประกอบการ“!” เรียกว่าแฟคทอเรียลซึ่งหมายถึงการคูณจำนวนทั้งหมดที่น้อยลงทั้งหมดผ่านหนึ่ง (เช่น 5! = 5 × 4 × 3 × 2 × 1) นิพจน์สำหรับ 5p3 ง่ายขึ้นถึง 5!/2! = 5 × 4 × 3 = 60
- สามสีสำหรับโปสเตอร์เดียว: กรณีเช่นนี้ที่สั่งซื้อไม่เรื่องเรียกว่ากการผสมผสาน- จำนวนชุดค่าผสมที่เป็นไปได้จะเป็นเพียงส่วนหนึ่งของจำนวนการเรียงสับเปลี่ยนที่เป็นไปได้ สำหรับกรณีที่มีห้าตัวเลือกที่จะเลือกสามตัวจะแสดงเป็น 5C3 และคำนวณเป็น 5!/[3! (5-3)!] = 5! / (3! × 2!) = 5 × 4 × 3 / (3 × 2 × 1) = 10
กรณีที่สองนี้มีความสำคัญต่อสามเหลี่ยมของ Pascal เนื่องจากสามารถคำนวณค่าได้ดังนี้:
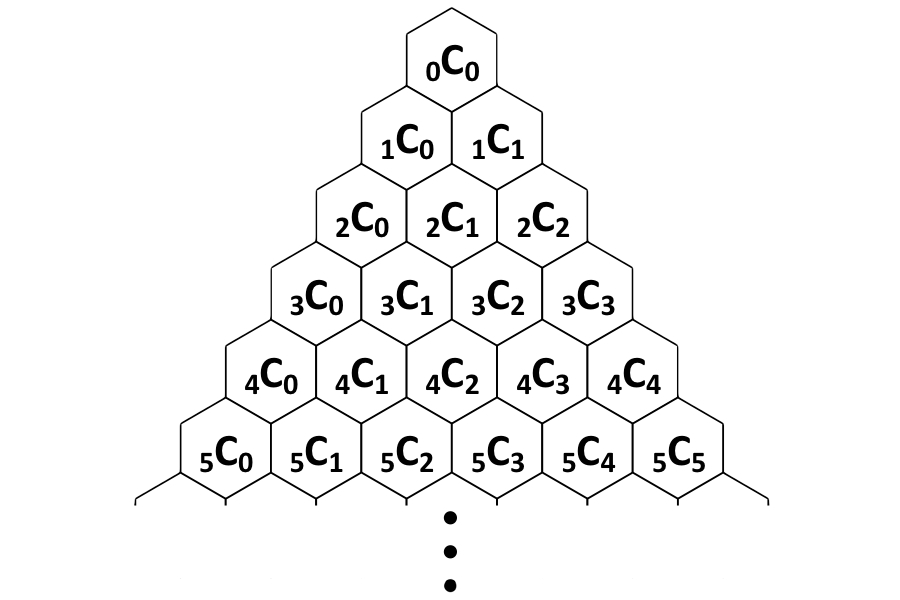
จากกระบวนการสร้างรูปสามเหลี่ยมของ Pascal เราจะเห็นหมายเลขใด ๆ สามารถสร้างได้โดยการเพิ่มตัวเลขสองตัวด้านบน ในทางคณิตศาสตร์นี้แสดงเป็นnCR-N-1CR-1-N-1CR- ความสัมพันธ์นี้ได้รับการบันทึกโดยนักวิชาการหลายคนของคณิตศาสตร์ตลอดประวัติศาสตร์
ทฤษฎีบททวินาม
ทวินามเป็นคำที่ใช้ในพีชคณิตที่หมายถึง“ สองสิ่งที่รวมเข้าด้วยกัน” ที่ทฤษฎีบททวินามหมายถึงรูปแบบของค่าสัมประสิทธิ์ (ตัวเลขที่ปรากฏต่อหน้าตัวแปร) ที่ปรากฏขึ้นเมื่อมีการคูณทวินามด้วยตัวเองหลายครั้ง ในทางคณิตศาสตร์นี้เขียนเป็น (x + y)n- สามเหลี่ยมของ Pascal สามารถใช้เพื่อกำหนดรูปแบบการขยายของค่าสัมประสิทธิ์ พหุนามที่ขยายตัวสองสามตัวแรกได้รับด้านล่าง
โดยใช้สัญลักษณ์รวมทฤษฎีบททวินามอาจเขียนได้อย่างชัดเจนว่า:
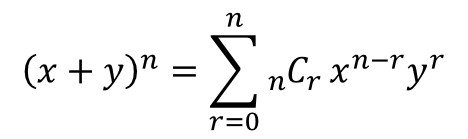
การกระจายแบบทวินาม
สำหรับกระบวนการที่น่าจะเป็นที่มีผลลัพธ์สองประการ (เช่นการพลิกเหรียญ) ลำดับของผลลัพธ์จะถูกควบคุมโดยสิ่งที่นักคณิตศาสตร์และนักสถิติเรียกว่าการกระจายแบบทวินาม- สิ่งนี้ยังเกี่ยวข้องกับสามเหลี่ยมของ Pascal
ตัวอย่างเช่นสำหรับการพลิกเหรียญสามใบมี 2 × 2 × 2 = 8 ลำดับหัว/หางที่เป็นไปได้ เมื่อจัดเรียงเป็นกลุ่มของ“ กี่หัว (3, 2, 1 หรือ 0)” แต่ละกลุ่มจะถูกเติมด้วยลำดับ 1, 3, 3 และ 1 ตามลำดับ สังเกตว่าสิ่งนี้ตรงกับแถวที่สามของสามเหลี่ยมของ Pascal มันเป็นพิสูจน์แล้วเทรนด์นี้มีไว้สำหรับการพลิกเหรียญทั้งหมดและแถวของสามเหลี่ยมทั้งหมด
ตาม George EP Box ใน "สถิติสำหรับผู้ทดลอง"(Wiley, 1978) สำหรับการพลิกเหรียญจำนวนมาก (สูงกว่า 20) การกระจายแบบทวินามเป็นการประมาณที่สมเหตุสมผลของการกระจายปกติการกระจาย“ เส้นโค้งระฆัง” พื้นฐานใช้เป็นรากฐานในการวิเคราะห์ทางสถิติ การประมาณนี้ช่วยลดความซับซ้อนของการวิเคราะห์ทางสถิติของปรากฏการณ์อย่างมาก
ตัวอย่างทางกายภาพของการประมาณนี้สามารถเห็นได้ในไฟล์เครื่องถั่วอุปกรณ์ที่สุ่มเรียงกันเป็นถังขยะตามวิธีที่พวกเขาตกอยู่ในการจัดเรียงสามเหลี่ยมของหมุด เนื่องจากลูกบอลชนหมุดมีความน่าจะเป็นเท่ากันที่จะตกลงไปทางซ้ายหรือขวาความเป็นไปได้ของลูกบอลลงจอดไปทางซ้าย (หรือขวา) หลังจากผ่านหมุดจำนวนหนึ่งแถวตรงกับความเป็นไปได้ที่จะได้รับหัวทั้งหมด (หรือหาง) จากจำนวนเงินที่เท่ากัน หลังจากมีลูกบอลจำนวนมากพอที่จะรวบรวมสามเหลี่ยมด้วยnแถวของหมุดอัตราส่วนของจำนวนลูกในแต่ละถังnไทยแถวของสามเหลี่ยมของ Pascal
ลำดับ Fibonacci
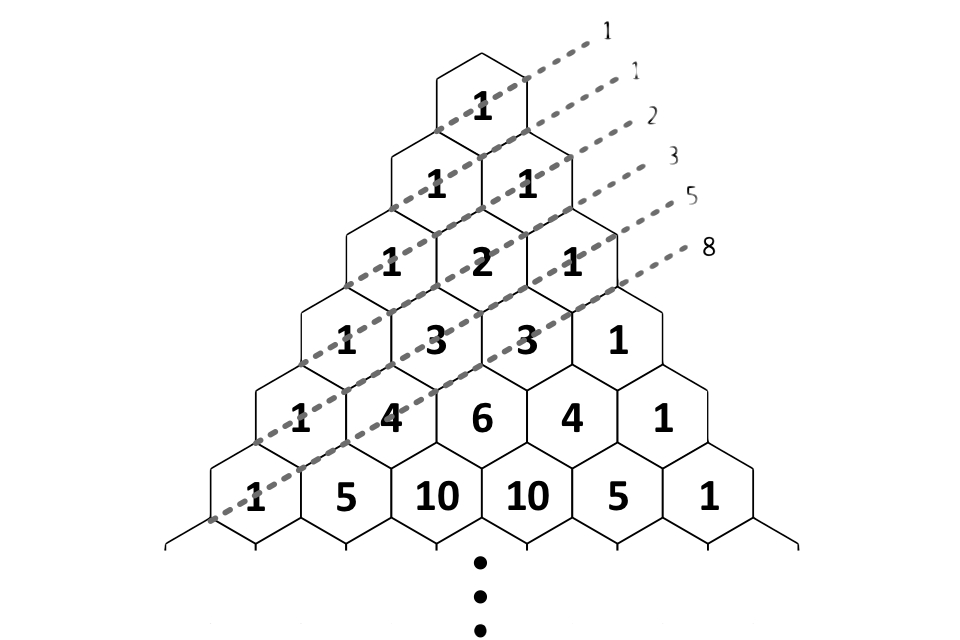
สามเหลี่ยมของ Pascal ยังมีความสัมพันธ์ที่สำคัญกับทฤษฎีจำนวน การเชื่อมต่อที่ชัดเจนที่สุดคือลำดับ Fibonacci- การเพิ่มจำนวนสามเหลี่ยมของ Pascal ในแนวทแยงบางอย่างจะสร้างจำนวนลำดับ
เศษส่วน
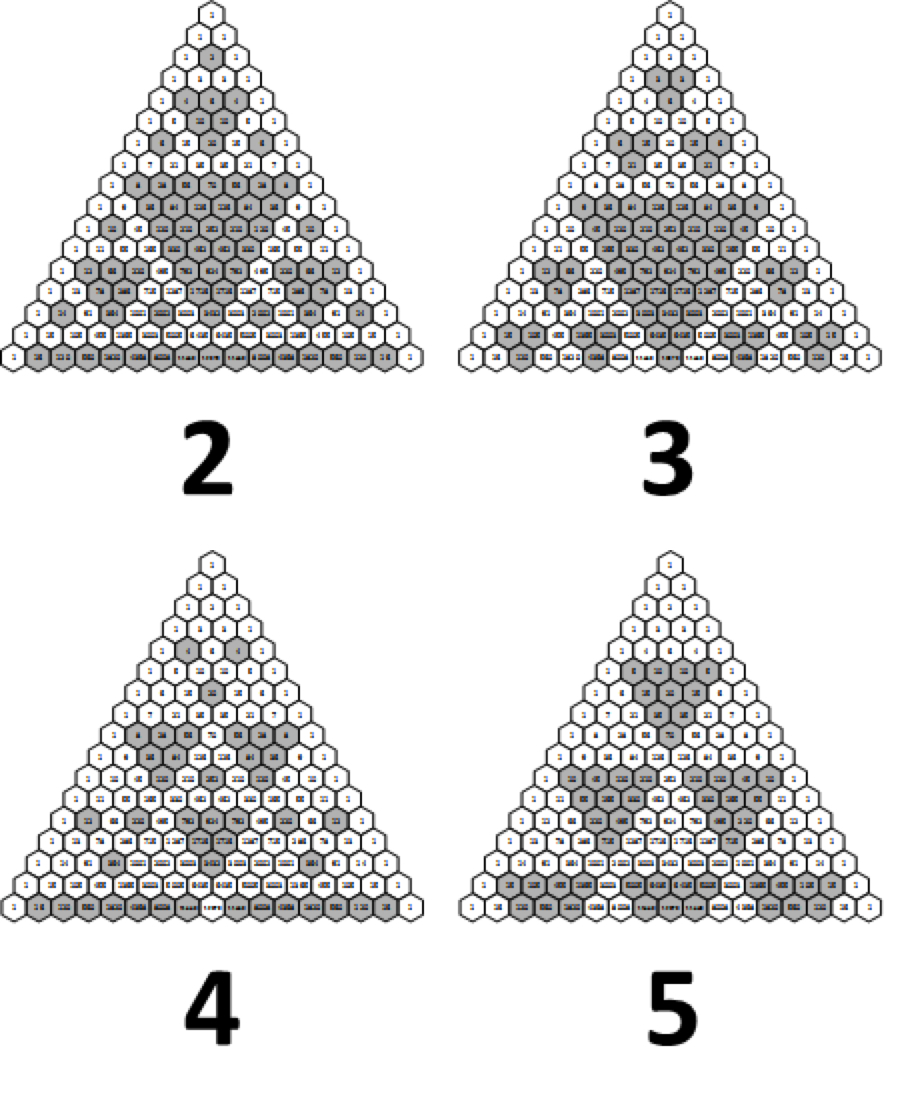
การระบายสีตัวเลขสามเหลี่ยมของ Pascal โดยการแบ่งแยกของพวกเขาทำให้เกิดความหลากหลายที่น่าสนใจเศษส่วน- โดยเฉพาะอย่างยิ่งการระบายสีตัวเลขทั้งหมดที่หารด้วยสอง (หมายเลขสม่ำเสมอทั้งหมด) สร้างสามเหลี่ยม Sierpin- รูปแบบเหล่านี้ปรากฏในศิลปะอิตาลีตั้งแต่ศตวรรษที่ 13 ตาม Wolfram Mathworld
ทรัพยากรเพิ่มเติม
สำหรับการอภิปรายเพิ่มเติมเกี่ยวกับสามเหลี่ยมของ Pascal ไปที่:





