ในโลกของคณิตศาสตร์ สองสิ่งที่ถือเป็นจริงเสมอ ประการแรก ปัญหาที่ดื้อรั้นและซับซ้อนที่สุดบางปัญหามักจะนำไปประยุกต์ใช้ในชีวิตจริงได้อย่างน่าประหลาดใจ และประการที่สอง สำหรับผู้ที่ใช้เวลาทั้งหมดจริงๆในโลกแห่งความเป็นจริง ปัญหาเหล่านั้นอาจดูเหมือน... เอาล่ะ-
ตัวอย่างเช่น “ปัญหาโซฟา”: ปริศนาที่ทำให้นักคณิตศาสตร์นิ่งงันมานานหลายทศวรรษ และยังได้รับการ “แก้ไข” โดยใครก็ตามที่เคยย้ายบ้านมาในชีวิต มันคือคำถามว่าจะขยับโซฟาโค้งเป็นมุม 90 องศาได้อย่างไร ใช่แล้ว เหมือนอย่างตอนหนึ่งของเรื่องเพื่อนตอนนี้คุณทุกคนกำลังพูดถึง
คณิตศาสตร์ของการย้าย
ในทางเทคนิคแล้วปัญหาเกี่ยวกับโซฟาคือสิ่งนี้: พื้นที่ของพื้นที่ที่ใหญ่ที่สุดซึ่งสามารถเคลื่อนตัวเป็นมุมฉากในทางเดินกว้างหนึ่งได้คือข้อใด มีการระบุอย่างเป็นทางการครั้งแรกในปี 1966โดยนักคณิตศาสตร์ชาวออสเตรีย-แคนาดา ลีโอ โมเซอร์ แม้ว่าจะเคยเป็นหัวข้อสนทนาเกี่ยวกับเครื่องทำน้ำเย็นทางคณิตศาสตร์มาหลายปีก่อนหน้านั้นแล้ว และจนถึงขณะนี้ก็ยังไม่มีข้อสรุปที่ชัดเจน
ตอนนี้ คุณจะสังเกตได้ว่าไม่มีการเอ่ยถึงเก้าอี้นวมที่มีชื่อเดียวกันในสูตรนี้ และจริงๆ แล้ว "เฟอร์นิเจอร์" ชิ้นแรกที่แนะนำในการแก้ปัญหาคือ "เปียโน" จริงๆ อย่างไรก็ตาม คำศัพท์เกี่ยวกับ “โซฟา” ก็เริ่มหมดไปในไม่ช้า ส่วนใหญ่เป็นเพราะ – เอาล่ะ ลองดูสิ:
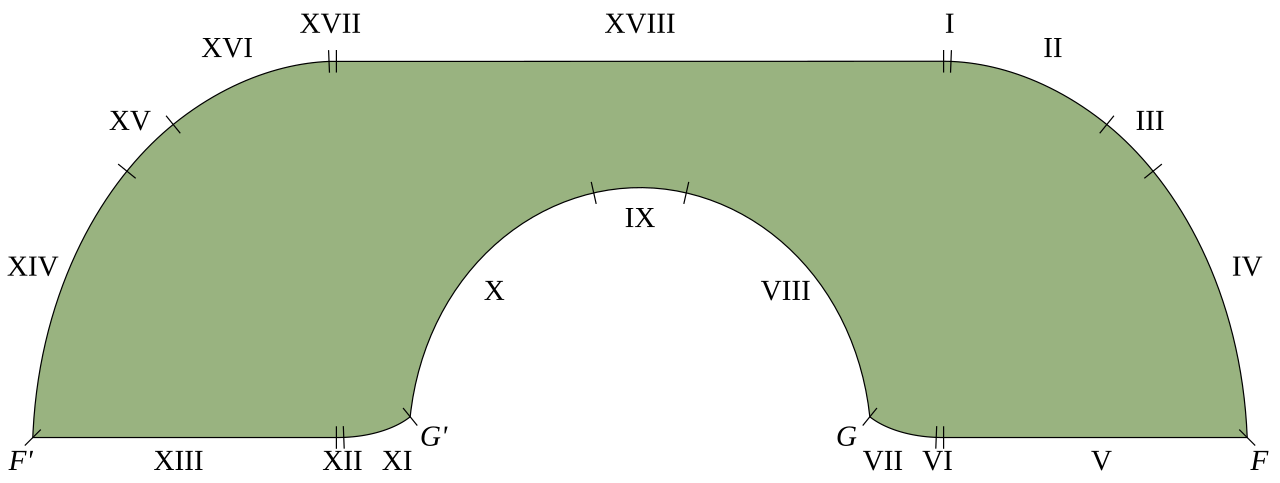
โซฟา Gerver แสดงแต่ละส่วนจากทั้งหมด 18 ส่วนประกอบกันเป็นขอบเขต
มันเป็นความมุ่งมั่นของขอบเขตล่างที่ทำให้เกิดรูปทรงโซฟาอันเป็นเอกลักษณ์: ในบทความปี 1968 ชื่อ เราล้อเล่นนะเกี่ยวกับการด้อยค่าของทักษะทางคณิตศาสตร์โดย 'คณิตศาสตร์สมัยใหม่' และโดยขยะทางปัญญาที่คล้ายคลึงกันในโรงเรียนและมหาวิทยาลัยจอห์น แฮมเมอร์สลีย์แสดงด้วยแคลคูลัสที่ค่อนข้างง่ายว่ารูปร่างนี้ให้พื้นที่ (π/2) + (2/π) – ประมาณ 2.2074
ที่จริงแล้วเขาไปไกลกว่านั้น ในรายงานฉบับเดียวกัน เขาพิสูจน์ว่าขอบเขตบนของพื้นที่กำหนดไว้ที่ 2√2 – ประมาณ 2.8284 เวลาผ่านไปเพียงไม่กี่ปี แต่ปัญหาโซฟากำลังมาถึงทางแก้ไขแล้ว ตัวเลขที่แน่นอนยังไม่ได้รับการแก้ไข แต่นักคณิตศาสตร์รู้ว่ามันต้องอยู่ระหว่างค่าสองค่านี้ แน่นอนว่าจะไม่ต้องใช้เวลาทำงานมากไปกว่านี้เพื่อค้นหาคำตอบที่แท้จริงใช่หรือไม่
ก้าวไปข้างหน้าอย่างรวดเร็ว 25 ปี ขอบเขตของแฮมเมอร์สลีย์ยังคงเป็นสิ่งที่ดีที่สุดที่เรามี จนกระทั่งนักคณิตศาสตร์ของ Rutgers Joseph Gerver ก้าวขึ้นไปบนจานโดยเสนอโซฟาที่สร้างขึ้นจากปี 18ส่วนโค้งที่เชื่อมต่อกัน ตามที่ทราบกันดีว่า “โซฟา Gerver” ได้เพิ่มขอบเขตล่างเป็น 2.2195
มันจะเป็นอีกสี่ศตวรรษอีกครั้งก่อนที่แนวทางแก้ไขที่เป็นไปได้ต่างๆ จะถูกลดทอนลงไปอีก:ในปี 2561นักคณิตศาสตร์ Yoav Kallus และ Dan Romik ใช้การพิสูจน์โดยใช้คอมพิวเตอร์ช่วยเพื่อโกนขอบเขตบนลงเหลือ 2.37
มันเป็นการปรับปรุงครั้งใหญ่จากขอบเขตเดิมของแฮมเมอร์สลีย์ – แต่วิธีแก้ปัญหาที่แน่นอนนั้นยังคงหลบเลี่ยงการจับกุม
แบคอยู่ในเกม.
คงจะเป็นเวลาประมาณเดียวกันกับที่ Kallus และ Romik กำลังหาวิธีแก้ปัญหา โดยที่ Jineon Baek นักวิจัยหลังปริญญาเอกที่มหาวิทยาลัย Yonsei ในกรุงโซล ประเทศเกาหลี เริ่มคิดถึงปัญหาโซฟาเป็นครั้งแรก เจ็ดปีต่อมา เขาคิดว่าเขาได้ถอดรหัสมันแล้วด้วยหลักฐานที่ยังไม่ได้รับการตรวจสอบจากผู้ทรงคุณวุฒิ
“ผมทุ่มเทเวลาให้กับเรื่องนี้มาก โดยยังไม่มีการตีพิมพ์ใดๆ เลย” เขากล่าวนักวิทยาศาสตร์รุ่นใหม่- “ความจริงที่ว่าตอนนี้ฉันสามารถบอกกับโลกได้ว่าฉันได้ทำบางสิ่งที่มีคุณค่าต่อปัญหานี้ก็เป็นสิ่งที่ถูกต้อง”
สำหรับคำถามที่อธิบายและจินตนาการได้ง่ายมาก หลักฐานของ Baek ไม่ใช่การดำเนินการเล็กๆ น้อยๆ ด้วยความยาวมากกว่า 100 หน้า มันทำได้มากกว่าการใช้กำลังกับปัญหาหรือกำจัดพื้นที่ที่เล็กลงอย่างต่อเนื่อง Romik บอกกับ New Scientist ว่าเป็น "การพัฒนาที่ยอดเยี่ยม"
“ฉันรู้ว่าฉันไม่เคยทำแบบนี้ได้” Romik กล่าว “ฉันไม่รู้สึกเสียใจ หรือประมาณว่า ฉันจะพลาดสิ่งนี้ไปได้อย่างไร เพราะมันชัดเจนว่ามันไม่ใช่ความคิดแบบที่ฉันคิดว่าจะทำได้ [Baek] เพิ่งเข้ามาจากทิศทางที่แตกต่างไปจากเดิมอย่างสิ้นเชิง”
ข้อพิสูจน์เป็นดังนี้ ประการแรก Baek กล่าวว่าโซฟาที่เหมาะสมที่สุด ไม่ว่ามันจะเป็นอะไรก็ตาม จะต้องมีคุณสมบัติเฉพาะ 3 ประการ ต้องเป็นสีเดียว สมดุล และมีมุมการหมุน พาย/2. ขอย้ำอีกครั้งว่าสิ่งเหล่านี้ค่อนข้างเป็นเทคนิคในการให้คำนิยาม แต่โดยพื้นฐานแล้ว ต้องสรุปดังนี้: “โซฟา” ที่เราใช้มาจนถึงตอนนี้มีรูปทรงที่ใช่อยู่แล้ว
ประการที่สอง แบคเริ่มพิสูจน์เงื่อนไขว่าโซฟาตัวนี้จะเคลื่อนตัวเข้ามุมได้อย่างไร ซึ่งเป็นสิ่งเล็กๆ แต่สำคัญสำหรับการทำขั้นตอนสุดท้ายให้เสร็จสิ้น นั่นคือการกำหนดขอบเขตบนสำหรับพื้นที่ของโซฟาตัวนี้ จากนั้นแสดงให้เห็นว่ามันเท่ากับของเกอร์เวอร์ ขอบเขตล่าง
ถูกต้อง หลังจากผ่านไป 32 ปี ปรากฎว่าเกอร์เวอร์พูดถูกมาตลอด
“แน่นอนว่าฉันมีความสุขมากกับเรื่องทั้งหมดนี้” Gerver บอกกับ New Scientist “ฉันอายุ 75 ปี และแบคมีอายุไม่เกิน 30 ปี เขามีพลังงาน ความแข็งแกร่ง และเซลล์สมองที่รอดชีวิตมากกว่าฉันมาก และฉันดีใจที่เขาหยิบกระบองขึ้นมา ฉันมีความสุขมากเช่นกันที่ฉันมีชีวิตอยู่นานพอที่จะเห็นเขาทำสิ่งที่ฉันเริ่มต้นให้เสร็จ”
วางเท้าของคุณขึ้น
แล้วปัญหาโซฟาตอนนี้จบหรือยัง? ในทางเทคนิคแล้วก็ยังต้องรอดูกันต่อไป เช่นเดียวกับการพิสูจน์ทางคณิตศาสตร์ทั้งหมด จะต้องได้รับการตรวจสอบโดยผู้ทรงคุณวุฒิเพื่อความถูกต้อง ซึ่งเป็นกระบวนการที่ Baek หวังอย่างเงียบๆ
“ฉันไม่สามารถพูดได้ว่าฉันมั่นใจ 100 เปอร์เซ็นต์ เพราะเราเป็นมนุษย์ เราทำผิดพลาดได้” เขาบอกกับ New Scientist “แต่ถึงกระนั้นฉันก็พยายามอย่างเต็มที่เพื่อให้มั่นใจเท่าที่จะทำได้”
แต่หากคุณหวังที่จะแก้ปัญหาโซฟาด้วยตัวเองต้องผิดหวังกับข่าวนี้ จงจำไว้ว่า เนื่องจาก Baek นิยามโซฟาของเขาไว้อย่างเคร่งครัด คุณจึงสามารถเลือกรูปทรงที่แตกต่างออกไปสำหรับตัวคุณเองได้เสมอ
มันอาจจะไม่ดีเท่าโซฟาสำหรับห้องนั่งเล่นของคุณแน่นอน แต่ไม่มีอะไรหยุดคุณจากการไป... คุณอาจจะพูดว่า Baek ไปที่กระดานวาดภาพ
สามารถตรวจสอบหลักฐานได้บนเซิร์ฟเวอร์การพิมพ์ล่วงหน้า ArXiv-









