一个3700年历史的粘土平板电脑透露了古老的巴比伦人在希腊哲学家毕达哥拉斯(Pythagoras)诞生之前,了解了毕达哥拉斯定理(Pythagorean Therorem),他与这个想法广泛相关。
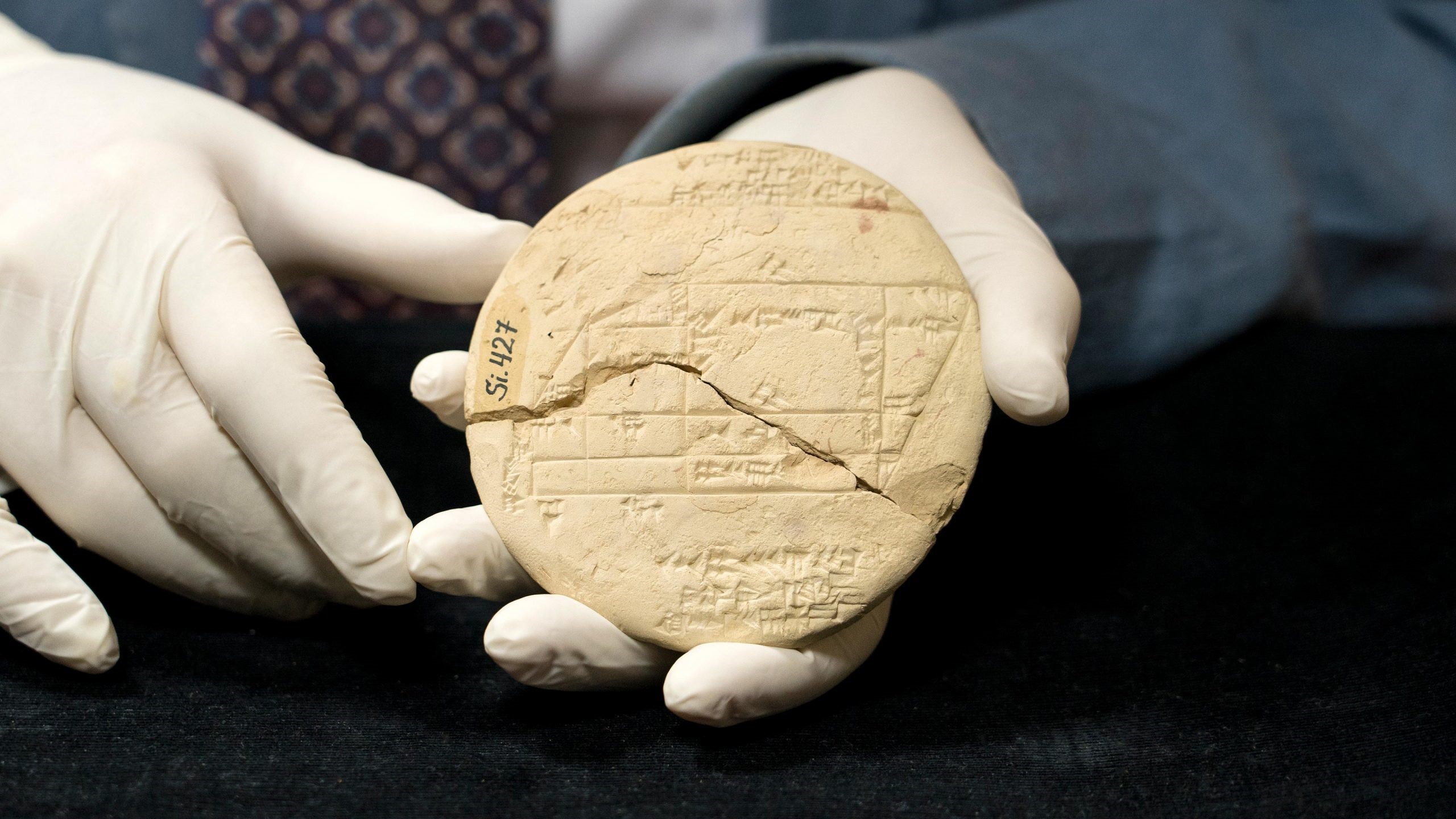
古老的土地测量师使用了称为SI.427的平板电脑来绘制准确的边界,并用楔形尺寸刻有数学表,该表构成了数学表,指示读者如何制作准确的右三角形。平板电脑是应用几何形状的最早的例子。
一场法国考古探险首先挖掘了平板电脑,该平板电脑的历史可追溯到1900年至1600年,现在在1894年的伊拉克,目前位于伊斯坦布尔考古博物馆。
但是直到现在,研究人员才发现了其古老标记的意义。
有关的:11个最美丽的数学方程式
“人们普遍认为,三角学 - 与三角研究有关的数学分支 - 由古希腊人研究夜空开发。”在一份声明中说。 “但是巴比伦人开发了自己的选择'proto-Trigonometry'来解决与测量地面有关的问题,而不是天空。”
根据曼斯菲尔德(Mansfield)的说法,SI.427是旧的巴比伦时期的唯一已知例子,或者是用于定义土地边界的计划测量师。曼斯菲尔德说:“在这种情况下,它告诉我们有关在其中一些领域被卖掉后分裂的法律和几何细节。”
平板电脑详细介绍了一个带有各种建筑物的沼泽地,包括塔楼。平板电脑上刻有三组毕达哥拉斯的三元组:三个全数字,前两个平方的总和等于第三个正方形。 SI.427上刻有三元组为3、4、5; 8、15、17; 5、12、13。这些可能被用来帮助确定土地的边界。

尽管平板电脑并未以当今表达的熟悉代数形式表达毕达哥拉斯定理,但提出这些三元组将需要理解支配双方长度与斜边之间关系的一般原则。
2017年,曼斯菲尔德(Mansfield)从同一时期发现了一张名为Plimpton 322的平板电脑,他确定为包含另一个三角桌。但是直到他看到SI.427上的三元组合,他才能够拼凑出来,古老的巴比伦人正在使用基本的三角理论来拆分土地。
曼斯菲尔德说,SI.427被认为是Plimpton 322之前的预期 - 甚至可能启发了它。
曼斯菲尔德说:“有一个整体的右三角形动物园,具有不同的形状。但是,巴比伦测量师只能使用很小的少数动物园。Plimpton322是对这个动物园发现有用形状的系统研究。” “这是从一段开始成为私人的时期 - 人们开始以'我的土地和您的土地'的方式思考土地,希望建立一个适当的边界以建立积极的邻居关系。这是这片平板电脑立即说的。这是一个领域。
尽管计算平板电脑上的土地边界的原因尚不完全清楚,但SI.427确实提到了一个质疑,即在一个名为Sin-Bel-Apli的著名人物和富有的女性土地所有者之间的约会境界。他说:“很容易看出准确性对于解决如此强大的人之间的争议有多么重要。”
即使在公元前570年的平板电脑的创建与萨莫斯毕达哥拉斯的诞生之间进行了1000年的发展 - 导致今天在学校教授正式的毕达哥拉斯统治学生 - 专家们早就知道,希腊人已经知道,希腊人从埃及人那里继承了数学教义,从埃及人和埃及人那里继承了埃及人。
然而,对于曼斯菲尔德来说,令人惊讶的是平板电脑的理论复杂水平揭示了古老的巴比伦人在人类历史的早期阶段所拥有的。
他说:“没有人期望巴比伦人以这种方式使用毕达哥拉斯的三倍。” “这更像是纯粹的数学,灵感来自当时的实际问题。”
最初发表在现场科学上。