二十五年来帮助罗斯把他的新沙发搬进他的公寓已经太晚了“朋友们,”一位数学家终于解决了恼人的“沙发问题”。
数学问题描绘了可以容纳给定宽度的角落的最大尺寸的沙发 - 这正是 1999 年播出的《老友记》一集中的角色所面临的问题。罗斯请求“旋转!”事实证明,如果他只考虑采用具有 18 个曲线部分且最大面积为 2.2195 单位的 Gerver 沙发,这种情况本来是可以避免的。 (好吧,也许它不会那么有帮助。)
现在,白真言韩国延世大学数学博士后研究员得出了答案。 Baek 于 12 月 2 日在预印本网站上发布了他的解决方案ArXiv。在 100 多页的数学证明中,Baek 发现,对于宽度为 1 个单位的走廊,想象中的沙发的最大面积可以是 2.2195 个单位——将答案从之前已知的 2.2195 到 2.37 个单位之间的范围精确缩小。该证明尚未在同行评审的期刊上发表,需要其他数学家进行研究以确定它确实是最佳的。
有关的:
格弗沙发上的“格弗”是数学家约瑟夫·格弗(Joseph Gerver),他是罗格斯大学的名誉教授,1992 年。但对于沙发是否可以更大一直存在争议,一个团队在 2018 年使用计算机辅助证明表明:2.37 实际上是上限。
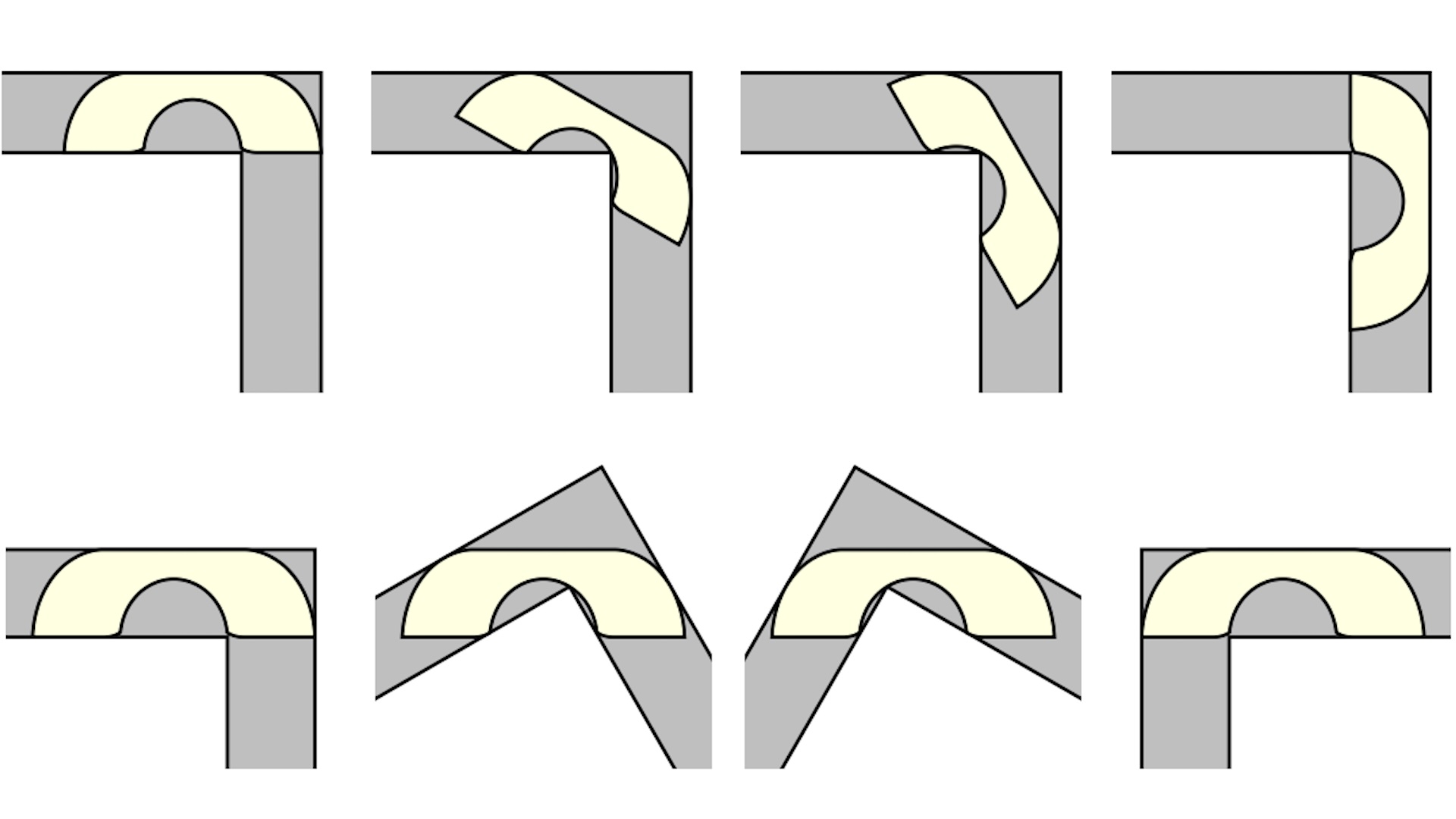
Gerver 的沙发是一张宽大的 U 形沙发,带有一个弯曲的“座椅”,可以挤在拐角处而不会被挂住。问题在于,这款精心设计的沙发(由 18 条独立的曲线组合而成)是否真的是能够实现转弯的最大、最优化的形状。 Baek 研究了形状的几何形状及其运动,发现 Gerver 的解决方案实际上是正确的。
该证据在社交媒体上引起了轩然大波。
“这是最佳的沙发,”用户@道德法律内12月6日,他在社交平台X上写道,贴出了一张相当宽臂沙发造型的照片。 “你可能不喜欢它,但这就是峰值优化的样子。”