研究人员利用模拟解决有限球体填充问题和“香肠灾难”

您是否曾经想过将有限数量的相同球体装入可变形的柔性容器（如凸包）的最佳方法？

特温特大学主动软物质实验室的研究人员由特温特大学 TNW 学院的 Hanumantha Rao Vutukuri 博士领导，并与乌得勒支大学合作，通过结合实验和. 他们的研究已经发布在自然通讯。

关于如何最好地包装一组球体，这是一个直观简单的问题，其研究历史可以追溯到 17 世纪。例如，英国水手雷利在试图找到一种在船上堆放炮弹的有效方法时，就考虑过这个问题。

后来，开普勒推测，无限数量的球体最密集的堆积方式是面心立方（FCC），类似于超市里看到的橙子和苹果的六边形排列。值得注意的是，这一假设直到 21 世纪才得到证实。

“香肠灾难”

当球体数量有限时，一切都会变得更加复杂；令人惊讶的是，将“有限”的球体包装成紧凑的簇并不总能产生最密集的包装。几十年前，数学家们就已经推测，线性、香肠状的排列可以提供最好的包装，但并不是所有数量的球体都是如此。

有一个奇怪的现象：香肠形排列是最有效的包装方式，但球体数量最多只能达到 55 个。超过这个数字，簇状排列就成为最佳包装方式。这种突然的转变被称为“香肠灾难”。

在三维空间中，最多 55 个球体线性排列会形成一个比任何簇排列都更密集的“香肠”。然而，在四维空间中，这种情况发生了巨大变化。大约需要 30 万个球体，“香肠”才能变成球形簇。

Rao 很好奇，这个有趣的问题是否可以在实验室中观察和解决，使用。这个系统包括微米级的球形颗粒（胶体）和巨型单层囊泡（GUV），它们作为柔性容器，是Vutukuri实验室的主要成分。

“这种好奇心促使我们通过 3D 实验探索有限球体填充问题，具体来说是在 GUV 中使用胶体。通过改变粒子的数量和囊泡的体积，我们能够使用共聚焦显微镜检查这些囊泡内的不同粒子排列。

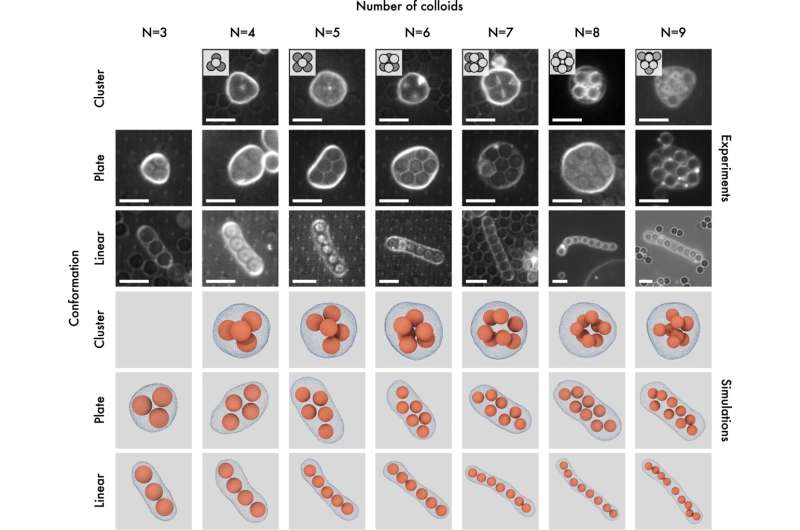
“我们确定了特定组合的稳定安排体积和粒子数：1D（香肠）、2D（板，粒子在一个平面上）和 3D（簇）。值得注意的是，我们还观察到了双稳态；配置在 1D 和 2D 排列之间或在 2D 和 3D 结构之间交替。然而，我们的实验仅限于观察最多 9 个粒子，因为填充大量粒子会导致囊泡破裂。”

Vutukuri 说，他们随后联系了乌得勒支大学的 Dijkstra 实验室，利用模拟深入研究了这个问题。令人惊讶的是，模拟预测，以香肠结构包装球体对于最多 55 个球体是最有效的。然而，当他们试图将 56 个球体装入囊泡时，他们发现紧凑的三维是更有效的安排。

值得注意的是，对于 57 个球体，堆积又恢复为香肠状。虽然数学家此前已确定香肠状结构对于 58 个和 64 个球体是最有效的，但他们的研究却与此相反，表明紧凑的簇更有效。

研究结果表明，数学家先前描述的现象“香肠灾难”不仅仅是一种理论上的场景，而且也可以通过实验观察到。