根據美國遺產詞典,流體動力學是“應用科學的分支,與液體和氣體的運動有關”。流體動力學是流體力學的兩個分支之一,即流體的研究以及力如何影響它們。 (另一個分支是流體靜態,它處理靜止的流體。)
多個領域的科學家研究流體動力學。流體動力學提供了研究的方法星星的演變,,,,洋流,天氣模式,板塊構造甚至血液循環。流體動力學的一些重要技術應用包括火箭發動機,風力渦輪機,石油管道和空調系統。
什麼是流?
液體和氣體的運動通常被稱為“流”,一個概念描述了流體的行為以及它們與周圍環境的相互作用,例如,水通過通道或管道移動或表面上。流量可以穩定或不穩定。在他的講義中,”基礎流體動力學的講座“(肯塔基大學,2009年)肯塔基大學工程學教授JM McDonough寫道:“如果流動的所有屬性都獨立於時間,那麼流程是穩定的;否則,它是不穩定的。 “也就是說,穩定的流不會隨著時間的推移而變化。穩定流動的一個例子是以恆定的速度流經管道。另一方面,從老式的手動泵中倒入的洪水或水是不穩定流量的示例。
流也可以是層流或湍流。層流流更光滑,而動蕩的流則更加混亂。確定流體流量狀態的一個重要因素是其粘度或厚度,其中較高的粘度會增加流量為層流的趨勢。猶他大學的工程學教授帕特里克·麥克默里(Patrick McMurtry)描述了他的在線課堂筆記的不同,”關於湍流的觀察“(猶他大學,2000年),說:“通過層流,我們通常指的是光滑,穩定的流體運動,在這種運動中,由於相對較強的粘性力,任何誘導的擾動都會受到抑制。在動蕩的流動中,其他力量可能會表現出粘度的作用。 ”
在許多情況下,例如在排水系統或飛機機翼中,層流是可取的,因為它效率更高,能量更少。湍流對於導致不同的流體混合或均衡溫度很有用。根據麥克唐納(McDonough)的說法,大多數感興趣的流動都是動蕩的。但是,這樣的流程可能很難詳細預測,並且區分這兩種類型的流程在很大程度上是直觀的。
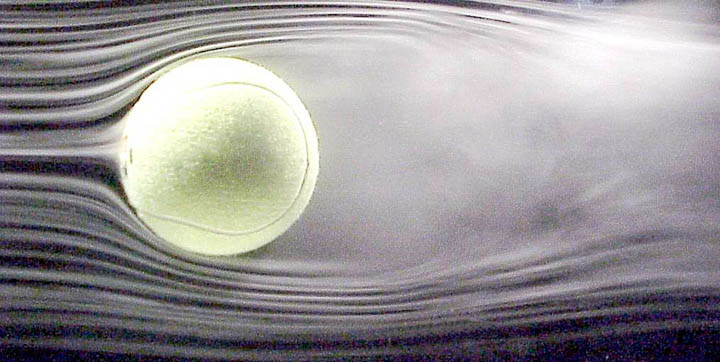
流體流動的重要因素是流體的雷諾數(關於),以19世紀的科學家奧斯本·雷諾茲(Osborne Reynolds)的名字命名,儘管該物理學家於1851年首次描述喬治·加布里埃爾·斯托克斯。麥克唐納給出了關於AS,“慣性與粘性力的比率”。慣性力是液體對運動變化的抗性,粘性力是由於流體的粘度或厚度而引起的摩擦量。注意關於不僅是流體的特性;它還包括其流量的條件,例如速度以及導管的大小和形狀或任何障礙物。
低關於,流動往往是光滑的或層流的,而在高處關於,流動往往是湍流的,形成渦流和渦流。關於可以用來預測氣體或液體如何在溪流中的障礙物周圍流動,例如橋樑堆積或飛機翼上的風。該數字也可以用於預測從層流到湍流的流動過渡的速度。
液體流
液體流量的研究稱為流體動力學。儘管液體包括各種物質,例如石油和化學溶液,到目前為止,最常見的液體是水,大多數用於流體動力學的應用都涉及管理該液體的流動。這包括防洪,城市水和下水道系統的運行以及可通航水道的管理。 [畫廊:夢幻圖像揭示了物理的美麗這是給出的
流體動力學主要涉及管道或開放通道中的水流。地質教授約翰·索斯德(John Southard)的講座從在線課程中註明,”流體運動簡介“(馬薩諸塞州技術研究院,2006年),概述了管道流量和開放通道流之間的主要區別:“在封閉的導管或頻道中流動(如管道或空氣導管)完全與剛性邊界接觸,而“在另一方面,“敞開的渠道流動”是那些在固定的範圍,是固體和泥濘的物質,他是一個固定的物質,他是一個重要的東西。雨後,水流,灌溉運河或水床單在地面上奔跑。”
由於這些邊界的差異,不同的力會影響兩種類型的流。根據斯科特(Scott)在他的書中的說法,”應用和計算流體力學,“(Jones&Bartlett,2009年),雖然封閉管道中的流動可能是由壓力或重力驅動的,但在開放通道中的流動僅由重力驅動。使用機械泵的壓力。

氣流
氣體的流量與液體流動有許多相似之處,但也有一些重要的差異。首先,氣體是可壓縮的,而通常認為液體不可壓縮。在 ”可壓縮流體動力學的基本原理“(Prentice-Hall,2006年),作者P. Balachandran描述了可壓縮的流體,說:“如果流體的密度在整個流場中明顯變化,則流動可能被視為可壓縮流動。 ”否則,流體被認為是不可壓縮的。第二,氣流很難受膜的影響。
日常生活中最常見的氣體是空氣。因此,科學家們非常關注其流量條件。風會導致空氣在建築物和其他結構周圍移動,也可以使泵和風扇移動。
特別感興趣的領域是物體通過大氣的運動。根據美國遺產詞典的說法,流體動力學的這個分支稱為空氣動力學,它是“相對於氣體移動的身體動力學,尤其是運動物體與大氣的相互作用”。該領域的問題涉及減少對汽車車身的阻力,設計更有效的飛機和風力渦輪機,並研究鳥類和昆蟲的飛行方式。
伯努利的原則
通常,以較高的速度移動的流體比以較低速度移動的流體更低。這種現象首先是由丹尼爾·伯諾利(Daniel Bernoulli)1738年在他的書中流體動力學,“通常被稱為伯努利的原理。它可以應用於在管道或通道或表面上移動的液體或氣體的速度。
該原理還負責飛機機翼上的升降機,這就是飛機可以飛行的原因。由於機翼在底部平坦並在頂部彎曲,因此空氣必須沿頂部表面的距離要比沿底部行駛更大的距離。為此,它必須更快地越過頂部,從而導致壓力減小。這使得機翼上的底部升降機上的高壓空氣。
流體動力學問題
科學家經常嘗試使用稱為流線,條紋線和途徑的數字來可視化流動。麥克唐納將流線定義為“流體中的連續線,使每個點的切線是該點速度向量的方向”。換句話說,流線顯示流動中任何特定點的流動方向。根據麥克唐納(McDonough)的說法,條紋線是“以前通過給定點的所有流體元素的位置[位置]”。他寫道,途徑(或粒子路徑)是“流體單個元素的軌跡”。如果流動不會隨時間變化,則該途徑將與流線相同。但是,在湍流或不穩定流動的情況下,這些線可能會大不相同。
流體動力學中的大多數問題太複雜了,無法通過直接計算來解決。在這些情況下,必須使用計算機模擬來通過數字方法解決問題。該研究領域稱為數值或計算流體動力學(CFD),該動力學(CFD)將其定義為“基於計算機的科學的分支,提供了流體流量的數值預測”。但是,因為湍流往往是非線性的,並且混亂在設置這些模擬的規則和初始條件時,必須特別注意。首先,小小的變化可能會導致結果差異很大。
可以通過將音量分為較小的區域並使用較小的時間步驟來提高模擬的準確性,但這會增加計算時間。因此,CFD應隨著計算能力的增加而提高。
吉姆·盧卡斯(Jim Lucas)是一位自由作家和編輯,專門研究物理,天文學和工程。他是盧卡斯技術。









