在數學中,二次的問題是一種處理可變本身的問題 - 一種稱為平方的操作。該語言源自正方形的區域,其側長本身乘以。 “二次”一詞來自正方形,拉丁語的正方形。
二次方程式是現實世界中大量現象的特徵,例如火箭船將在哪裡降落,對產品充電多少或一個人在河上上下划船的時間。由於它們的應用多種多樣,二次學具有深遠的歷史重要性,並且是基礎的代數的歷史。

拋物線
四邊形的數學與稱為拋物線的U形曲線本質上相關。也許最熟悉的例子是從飲水噴泉中射出的水流。還有許多其他例子,例如衛星盤的橫截面或懸架橋上的電纜。
對於許多古希臘的數學家來說,拋物線是一個重要的形狀,例如亞歷山大的歐幾里得(〜300 bc),錫拉丘茲的阿基米德(公元前287-212 BC),佩爾加的阿波羅尼烏斯(262-190 bc)和亞歷山大(Ad 290-350)和帕普斯。這些學者指出了許多數學特性固有的拋物線:
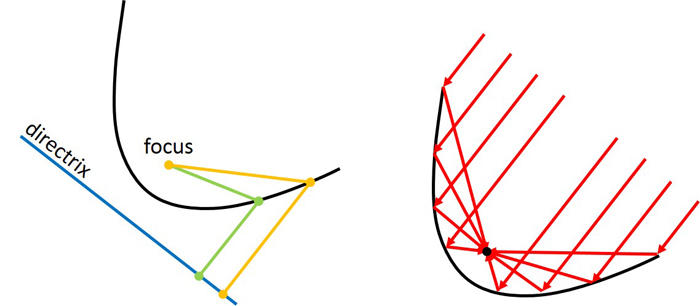
1。拋物線是遠離點的一組點(a重點)和一行(aDirectrix)。適當命名的焦點在許多現代工程應用中很重要,因為這是拋物線盤中反映傳入波的重點,無論是無線電波(如衛星盤中),光線(如濃縮太陽陣列中)還是聲音(如在拋物線片中)。
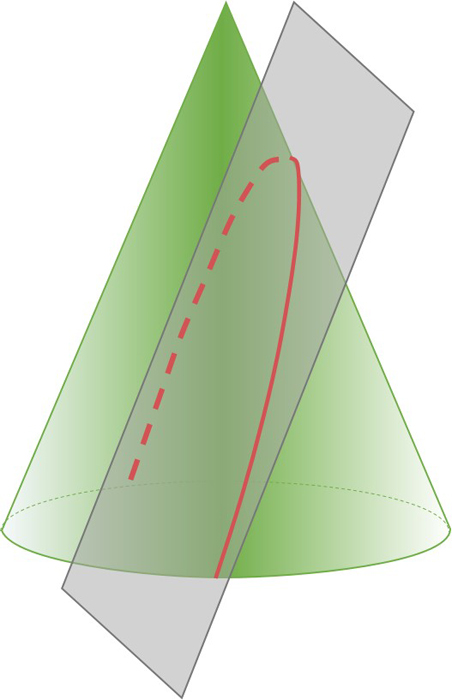
2。拋物線也通過與錐側斜坡平行的錐體切割來產生。因此,拋物線在一組數學曲線中稱為圓錐部分。在這一發現後將近2000年可以吸引拋物線的指南針。
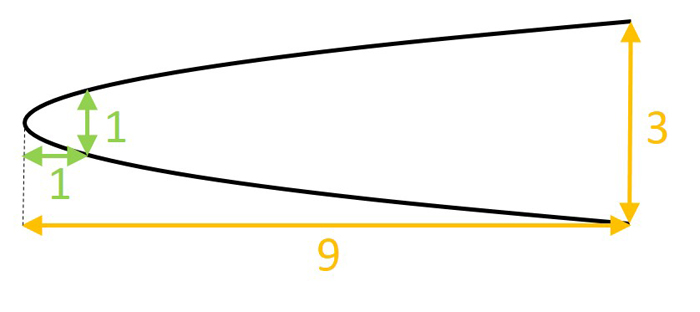
3。拋物線的高度變化與該拋物線寬度的正方形變化成正比。例如,如果拋物線是一個單位寬的一個單位,則在三個單元寬的地方將是九(三個平方)的單位。正是由於這個屬性,Apollonius從寓言,在“應用”的意義上,希臘語“應用”的詞正在“應用於”(乘以)本身。這是將拋物線的形狀與二次數學概念聯繫起來的屬性。
儘管拋物線無處不在,但重要的是要注意,它們與其他U形曲線不同,例如懸掛鍊(catenary),孩子在鞦韆(圓形弧線)上的路徑,弧光燈從直立的手電筒上閃閃發光的牆壁(純曲(A骨)或彈簧側視圖(Sinusoid)的側視圖)。這些其他曲線沒有前面提到的拋物線屬性。
彈丸運動
在16世紀,拋物線與四次數學之間的聯繫至關重要,當時歐洲文藝復興時期的學者註意到,諸如砲彈和迫擊砲等彈丸以拋物線軌跡旅行。那個時代的許多著名科學家,包括萊昂納多·達·芬奇和伽利略·伽利略(1564-1642)彈丸運動。根據紐約市城市大學歷史教授約瑟夫·道本(Joseph W. Dauben)(CUNY),因為文藝復興時期的藝術家痴迷於準確的現實在藝術中,伽利略類似地迷戀著準確的現實使用 數學。 1638年,伽利略出版第一個證明地球重力的均勻加速會導致彈丸移動拋物線軌跡。數學可以用來描述運動是科學革命進步的關鍵。
四邊形的圖
大約與伽利略,法國哲學家和數學家雷內·笛卡爾(RenéDescartes)(1596-1650)發表了“laGéométrie”(1637年),該領域描述了一個稱為分析幾何學領域的圖形代數方程技術。今天仍然使用了他的方法的變體。如下所示,二次方程的圖是拋物線。
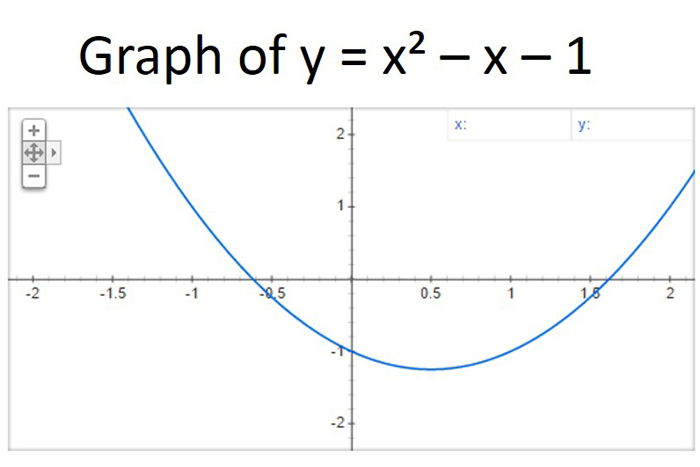
古老的二次:黃金比率
要了解數學家,科學家和工程師今天使用的二次解決方法,讓我們探索一個古老的數學問題:黃金比率。順便說一句關於黃金比率的誤解“(1992年),緬因州大學的數學教授喬治·馬爾科夫斯基(George Markowsky)指出,黃金比率的歷史意義和美學吸引力通常被誇大了,儘管實際上該比率通常與&&&&&&&&斐波那契序列),幾何(例如二十面體)和生物學(例如植物葉之間的角度)。
因此,確定了一種確定黃金比率的方法:
找到具有長度和寬度的矩形,使得在矩形的一端切開正方形時,其餘的廢矩形將具有與原始矩形相同的形狀或“縱橫比”(但以直角旋轉)。
而古希臘人解決了這個問題使用幾何形狀,我們使用代數正如今天所教的。
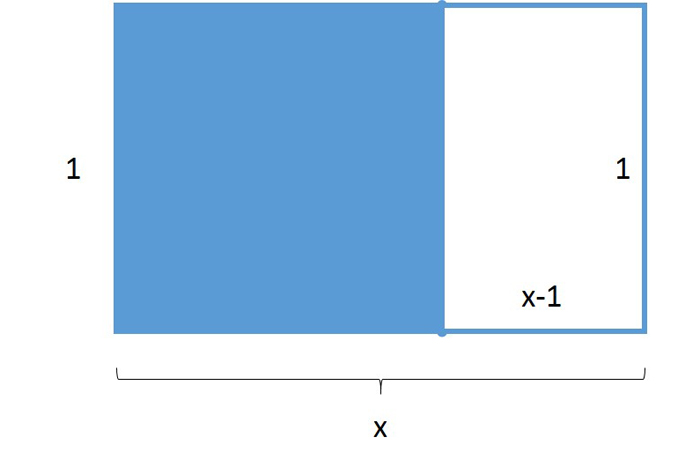
為了確定長度和寬度將產生黃金比例,我們給短側的長度為1,而長側則x長度為x。因為將縱橫比定義為長側除以短邊,所以該矩形的縱橫比為x/1,或簡單地x。如果我們從該矩形上切斷一個正方形,則其餘的廢料的長度長度為1,而短長的長度為x - 1。因此,縱橫比為1/(x - 1)。了解總矩形和較小的廢矩形的縱橫比應該相同,我們的方程式為x = 1/(x - 1)。
二次公式
這是指示學生今天解決此方程式的方式。從等式開始:
x = 1/(x - 1)
將方程的每一側乘以表達式x - 1:
x·(x - 1)= 1
在表達式x - 1::分佈x。
X·X - X·1 = 1
變量x乘以本身為x²。這種平方使等式成為二次:
x² - x = 1
現在,我們從等式的每一側減去1,以實現二次方程的標準形式:
X² - X - 1 = 0
同等地,這可以寫為:
(1)·x² +(-1)·x +(-1)= 0
將其與方程式A·x² + b·x + c = 0進行比較時,它給出了a = 1,b = -1和c = -1的值。這些值在二次公式中使用為
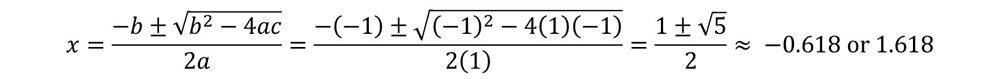
符號“±”的意思是“ plus或sinus”。因此,二次公式總是提供兩個解決方案。將這些值中的任何一個替換為等式x = 1/(x - 1),以測試這是否使方程式的兩側都相同。它確實如此,這意味著該方法有效。請注意,這些值也是方程式(y =x² - x - 1)的標準形式圖的位置,橫穿x軸,x軸是y = 0的位置(請參見上圖)。在這種情況下,正值具有更大的物理意義,因為矩形不應具有負寬度。
古代巴比倫的起源
為了了解二次配方的來源以及為什麼起作用的洞察BM 13901,大英博物館)。根據雅克·塞西亞諾(Jacques Sesiano)的說法代數史介紹”(AMS,2009)該平板電腦的第一個問題大約轉化為:
我添加了正方形的區域和側面以獲得¾。廣場的一側是什麼?
該問題用現代符號寫為:
x² + x =¾
以下是Sesiano所述的巴比倫和阿拉伯方法的重述。首先,我們將翻譯巴比倫人使用的步驟,但也將其轉化為我們今天在代數中使用的象徵性語言。完全象徵性的語言在17世紀首次出現在歐洲。因為巴比倫人不知道負數,所以有必要以x的形式編寫方程式2+ px = q,其中p = 1和q =¾。將其與現代標準形式斧頭進行比較時2& + bx + c = 0,它表明p = b/a和q = -c/a。
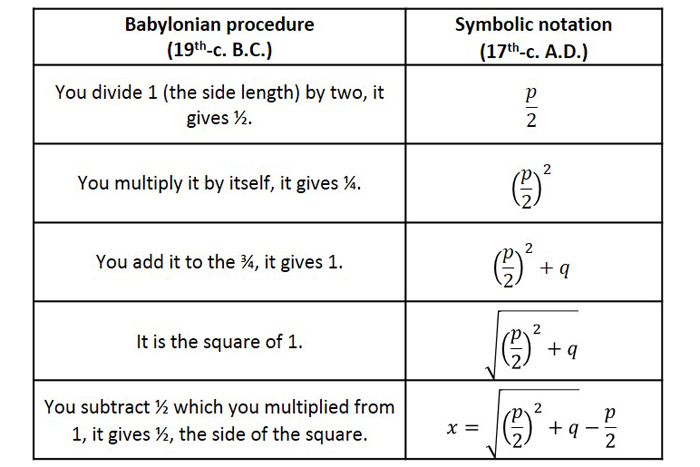
現在讓我們得出證明該過程是正確使用幾何方法的正確方法是正確的,就像阿拉伯數學家在第九世紀的公元中所做的那樣,以下是一個證明的變化,在波斯數學家al-khwārizmī出版的出版《通過完成和平衡的錄音》和《貶低》的記錄中,關於“完成和平衡”的撰寫效果。伊斯蘭的黃金時代是從七世紀中葉到13世紀中葉的時期,當時穆斯林統治了一個從中亞到北非和伊比利亞的帝國。
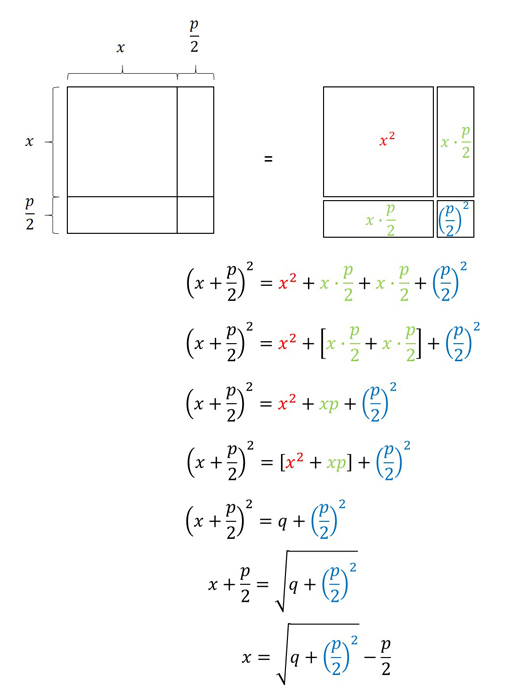
如果我們“插入” p = b/a和q = -c/a,則該公式確實可以簡化為二次方程的現代形式,如今天所教的。
各個年齡段的二次配方在非洲裔歐亞氏菌中使用了各種形式。巴比倫人和埃及人在公元前19世紀左右使用了程序版本,即公元前七世紀的迦勒底人,公元前四世紀的希臘人和公元五世紀的印第安人在公元五世紀的言辭和同步形式是由阿拉伯人在九世紀二手和歐洲的進步中開發的,以及在歐洲的範圍內,以及在11世紀的融資中,以及11世紀的方法,以及11世紀的方法,以及11世紀的方法,以及11世紀的方法關於負,非理性,虛構和復數。
其他資源