拓撲是數學的一個分支,它描述了數學空間,尤其是源於空間形狀的屬性。許多形狀拓撲師都非常奇怪,以至於幾乎所有日常物品(例如碗,寵物和樹木)構成了少數群體。 “拓撲”一詞源自希臘語的地方(拓撲)和研究(- 學)。
拓撲是在多個研究領域的指導中很重要的:
- 理論物理學(特別是量子力學例如量子場理論和弦理論)
- 宇宙學(用於確定宇宙的形狀)
- 生物學(用於DNA的纏結並預測器官和其他身體部位的生長)
- 計算機科學(用於確定數據集的大規模結構)
- 機器人技術(在機器人臂的運動基礎上根據空間的形狀進行了多個維度等於臂接頭數的形狀)
連續變形
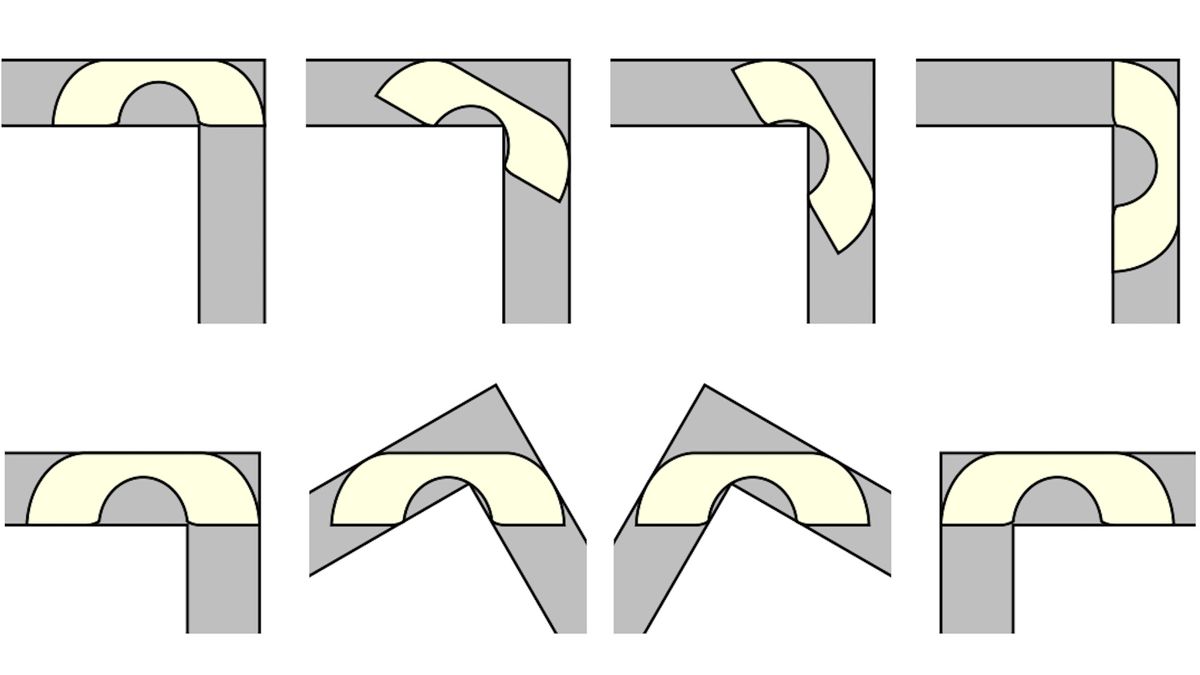
拓撲學家研究形狀的特性,尤其是在形狀扭曲,拉伸或變形後保留的拓撲特性。此允許更改的列表在數學概念下都被稱為連續變形,這大致意味著“伸展,但不撕裂或合併”。例如,可以將一個圓圈拉到橢圓形或諸如手印輪廓之類的複合物中。撕裂和合併是因為所謂的不連續,所以他們不允許。
兩個可以伸展到同一形狀的物體被描述為同型,來自拉丁語希臘語的“類似”(同源)和希臘語“形式,形狀或圖形”(Morphe)。通過這個鏡頭,幾乎所有日常物體都是同質的,帶有球(一個球)或各種圓環(甜甜圈)。
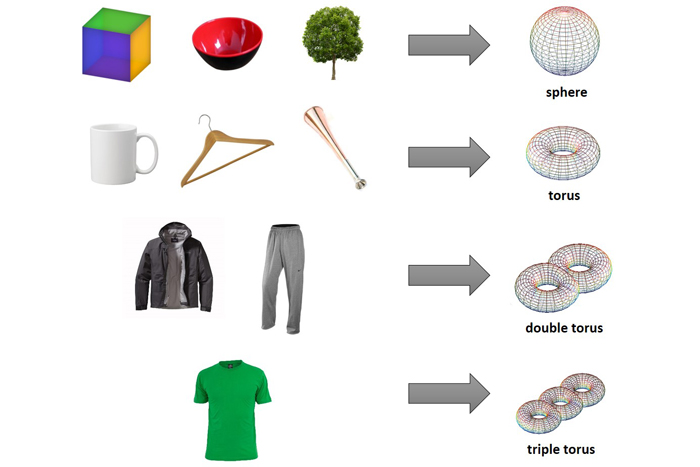
拓撲的某些分支使對像在伸展時可以通過自身;其他人沒有。考慮表面能通過自身,重要的是不要無限緊繃,因為這也增加了不連續性。通常,當表面重新向後翻倍時,例如試圖將球體向外旋轉時(這很困難,但可能)。
歐拉的特徵
在連續變形下不變的屬性的一個示例是對象的歐拉的特徵,以18歲的Leonhard Euler的名字命名Th- 世紀德國數學家。
為了展示物體的歐拉特徵,首先,我們取下一個球(或帶有球體的物體同構物體,例如人頭),然後用多邊形在表面上瓷磚。然後,我們計算面部(側面),邊緣(兩個側面相遇的地方)和頂點(三個或三個側面相遇的地方)的數量。現在,添加面(F)和頂點(V)的數量,並減去邊緣(E):F + V - E的數量。答案總是一樣:兩個。由於五個柏拉圖固體(由一種常規多邊形製成的3-D形狀都是同態的,因此它們也具有兩個歐拉的特徵。
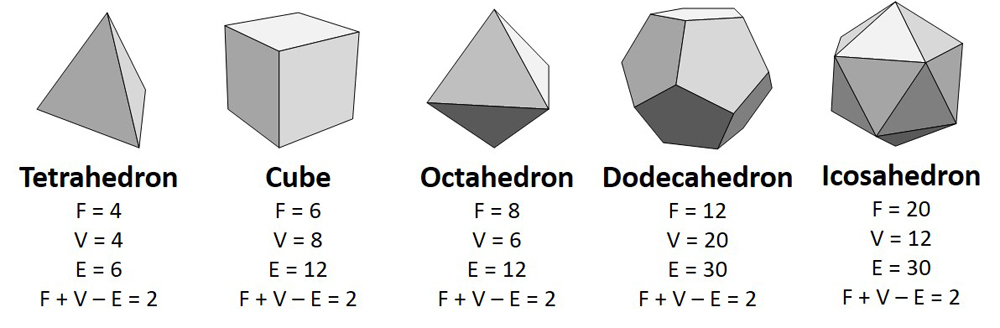
如果我們考慮添加邊緣或頂點的含義,那麼我們就可以理解為什麼歐拉的特徵得到保存。在兩個頂點之間添加一個邊緣將一張臉分成兩面:邊緣增加一個,臉部增加一個,頂點保持不變。同樣,沿邊緣添加一個頂點將邊緣分為兩個:邊緣增加一個,頂點增加一個,並且面保持相同。
現在,曲線的表面,count f,v和e的表面,您將獲得零的特徵。這是一個例子:
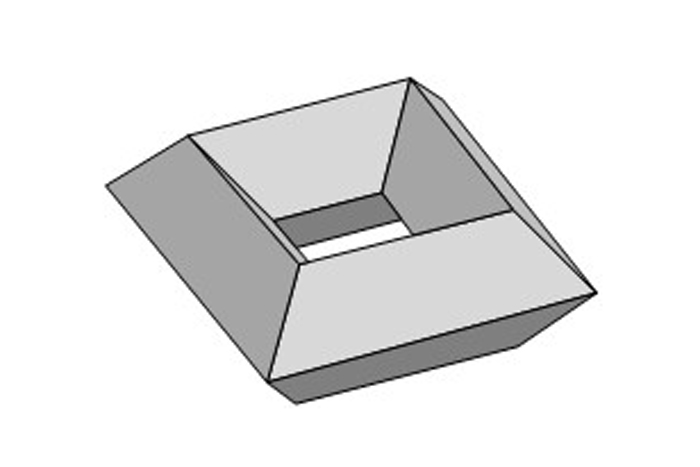
用雙帶,歐拉的特徵為負兩個。對於三重圓環,負四。每個額外的孔可將歐拉的特性減少兩個。
不可定向的表面
到目前為止,我們談論的所有形狀的一件事是,據說它們是可調節的。這意味著在外表面上行走的錯誤將始終留在外面。內部也是如此。也有不穩定表面,這意味著表面上流浪的錯誤最終都可以在兩側。最著名的例子是Mobius Strip(其具有零的EULER特性,EC = 0)。

儘管“莫比烏斯脫帶的雙方”之類的語言對於介紹該概念很有用,但它與拓撲學家的思想背道而馳,他說任何表面都是2-d,而居住的人也是如此。通過這種鏡頭,想到生活在表面本身中的2D錯誤更有用。對於可定向的表面,有右手錯誤和左手錯誤,但是對於不可定向的表面,右手和左手的錯誤是無法區分的。這強調了Mobius帶代表一個空間,我們對源於該空間形狀的特性感興趣。
基本多邊形
以這種表面為2-D的觀點,可以方便地表示拓撲空間基本多邊形。要將基本多邊形的2-D表面變成3-D對象,請拉伸表面,以便相應的側面與箭頭指示的方向相連。可以看出,連接平行的邊是一個圓柱體(EC = 0),並且連接反行線使Mobius帶(EC = 0)。
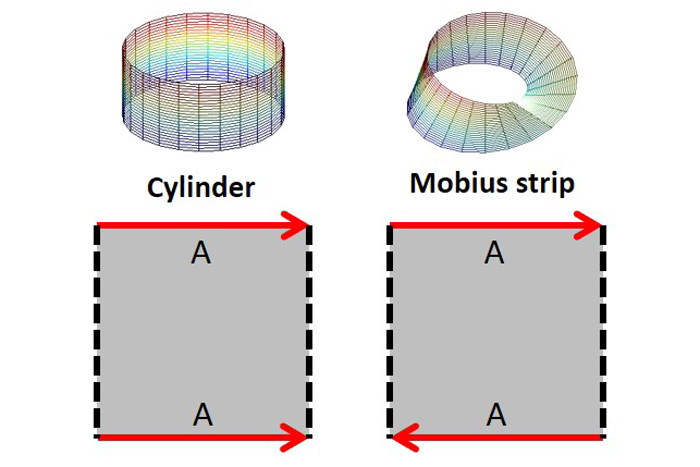
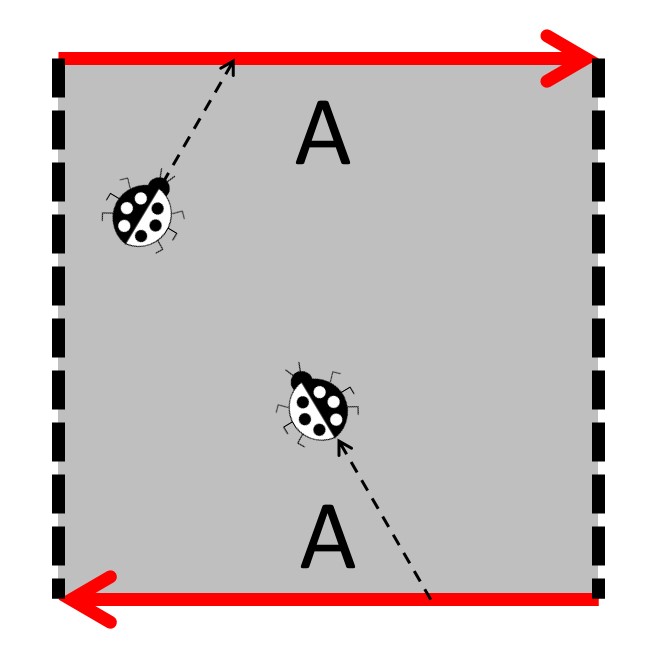
一個基本多邊形的箭頭和箭頭邊界的二維錯誤被運輸到另一個邊界,與箭頭方向相比,以相同的方式定向。該錯誤是否保持相同或翻轉表示表面是可定向還是不可定向。不允許二維錯誤越過虛線邊界。
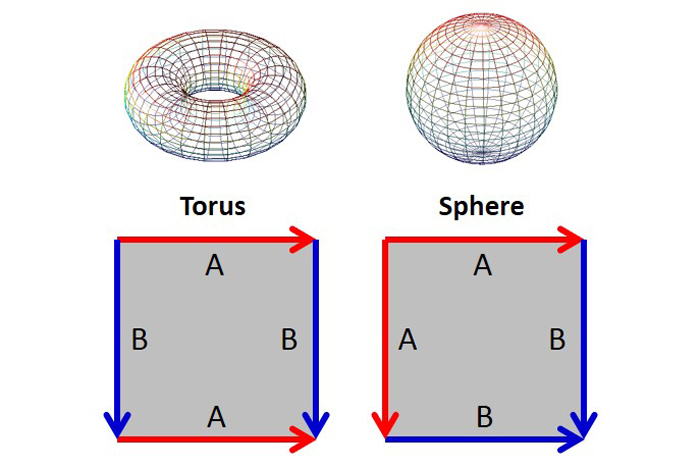
我們談論的最初形狀也具有基本的多邊形。要製作圓環,首先製作一個圓柱體,然後伸展圓柱的末端,直到它們相遇為止。要製作一個球體,請從角落到角落折疊紙張以製作一個三角形的信封,然後將其充氣直至球形。
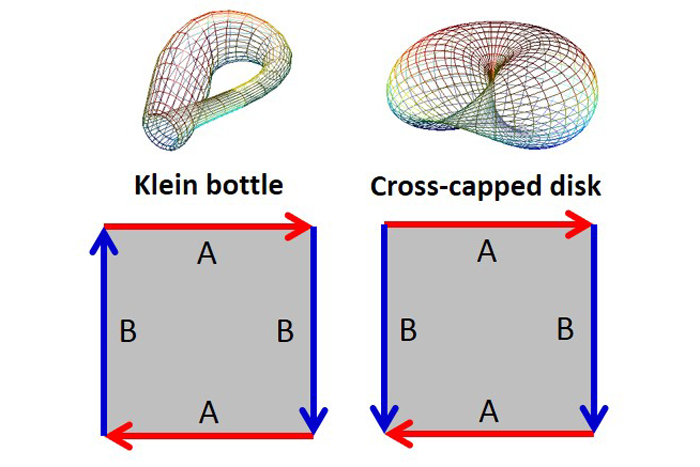
可以通過兩種不同的方式組合莫比烏斯帶的虛線邊緣,以產生兩個不可方向的表面:可以將klein瓶(EC = 0)視為莫比烏斯帶和圓柱之間的交叉,並且可以將一個交叉式磁盤(EC = 1)視為兩個Mobius Strips之間的交叉。與Mobius帶一樣,如果有第三個維度可以包含這張地圖,我們可以從空間的整體“形狀”中獲得一些視角。兩種結構都要求允許表面通過自身。二維錯誤不會注意到這樣的交叉點;只有在二維空間中走某些路徑後,世界才“翻轉”。
拓撲中的著名問題
拓撲已經存在了幾個世紀,但已經有一個有自己的故事的問題和子領域的悠久歷史。
- 科尼格斯伯格的七個橋樑:經常被認為是拓撲中的第一個問題。古老的普魯士小鎮科尼格斯伯格(Königsberg)曾經有七座橋樑,其人民想知道是否可以走一條只越過每座橋的小路。 1735年,歐拉(Euler)證明這樣的道路是不可能的。
- 手掌和指紋的圖案:指紋都具有常見的特徵,例如循環和triradii(三線匯聚在一起)。 1965年,英國醫學遺傳學家萊昂內爾·彭羅斯(Lionel Penrose)指出,指紋和棕櫚印花遵守普遍的規則:每個人出生的五個手指的人總是比循環多四個。
- 毛茸茸的球定理:對於被頭髮覆蓋的球(或球形),不可能將所有頭髮梳理。必須至少有一個地方伸直頭髮。
- 球體勢頭:對於允許通過自身的球形表面,是否有可能在不捏任何區域無限緊身的情況下將球體完全轉動?這很棘手,但是是的。
- 結理論:結理論是拓撲內的一門學科,只涉及無法通過自己或他人的托里(複數)。結理論的主要重點是確定兩個外觀的結是否是同態。
- 龐加萊的猜想:在本文中,我們只檢查了2D空間,但是還有一些以奇怪方式連接的3D空間。這龐加萊的猜想,最初於1904年首次擺姿勢,是關於這些3D空間的,指出“每個簡單連接的,封閉的3個manifold都是同型3-Sphere。”近一個世紀後,2000年粘土數學學院選擇了七個未解決的“千年獎”問題,其中100萬美元將被授予任何找到解決方案的人。龐加萊的猜想是第一個要解決的問題。俄羅斯數學家格里戈里·佩雷爾曼(Grigori Perelman)於2002年找到了解決方案,他拒絕了千年現金獎和田野獎章(許多人認為等同於諾貝爾的數學獎)。
其他資源