
當今,各地的數學書呆子都在挖掘一片餡餅,以慶祝其最具標誌性的非理性數字:pi。畢竟,3月14日或3/14是紀念基本數學常數的最佳時機,其第一位數為3.14。
pi或π是圓的圓周與直徑的比率。因為它是非理性的,所以不能將其寫成一小部分。相反,它是一個無限長的,不重複的數字。
但是,如何發現這個非理性的數字,經過數千年的研究,這個數字仍然有任何秘密嗎?從這個數字的古代起源到其模糊的未來,這裡是關於PI的一些最令人驚訝的事實。
有關的:存在9個最大數字
記住pi

印度韋洛爾的拉傑維爾·梅納(Rajveer Meena)屬於印度韋洛爾(Rajveer Meena)的記憶最多的記錄。根據吉尼斯世界紀錄。 (截至2024年3月,Meena仍然保留此記錄。)以前,Chao Lu,中國根據吉尼斯世界紀錄,他在2005年將PI從記憶中朗誦至67,890個位置。
非官方的唱片持有人是Akira Haraguchi,他在2005年錄製了他在100,000個小數位PI的朗誦錄像中,最近又超過了117,000個小數位數,監護人報告。
數字愛好者已經記住了許多PI數字。許多人使用記憶輔助,例如被稱為piphilology的助記解技術,以幫助他們記住。通常,他們使用用pilish寫的詩(每個單詞中的字母數量與PI的數字相對應)。說哪個...
有一個pi“語言”

文學書呆子發明了一種稱為皮里什(Pilish)的方言,其中連續單詞的字母數量與pi的數字匹配。例如,邁克·基思(Mike Keith)在皮里什(Pilish)中寫下了《不喚醒》(Vinculum Press,2010)的書:
現在,我跌倒了,一個疲倦的郊區液體在樹下,與歐洲暮色的森林旁邊漂流。
(“現在”有三個字母,“我”有一個字母,“秋天”有四個字母,依此類推。)
指數增加
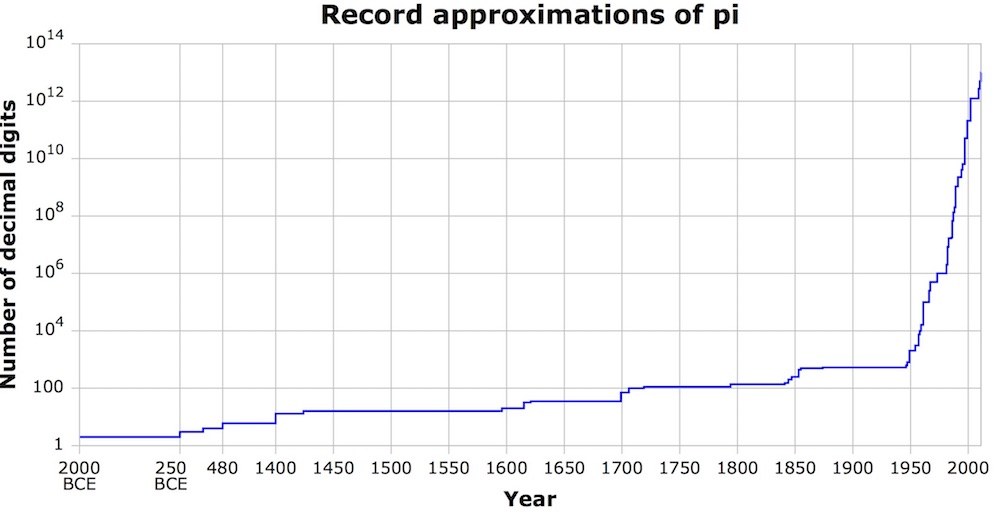
由於PI是一個無限的數字,因此,根據定義,人類將永遠不會確定PI的每個數字。但是,自PI首次使用以來,計算出的小數位數的數量已成倍增長。巴比倫人認為這是公元前2000年的3 1/8足夠好,而古代中國人和舊約的作家(國王7:23)似乎很高興使用整數3。但是到1665年,先生,先生艾薩克·牛頓已將PI計算為16個小數點。到1719年,法國數學家托馬斯·芬特·德拉格尼(Thomas Fantet de Lagny)計算了127個小數點,根據“ PI史”(St. Martin's Press,1976年)。
這計算機的出現從根本上提高了人類對PI的了解。根據“ PI的歷史”(St. Martin's Press,1976年),在1949年至1967年之間,PI的已知小數從Eniac計算機上的2,037飆升至巴黎CDC 6600的500,000。
當然,最新的計算將這些早期記錄從水中吹出。
PI有史以來最多的數字
2021年,瑞士的研究人員使用超級計算機粉碎了現有的計算PI記錄。
團隊連續運行超級訓練者108天計算為超過62.8萬億個小數的PI,將以前的計算記錄吹到十二萬億個小數位。那是很多pi。
這種PI精度是前所未有的。但是,它可能會浪費在世界頂級科學機構之一上。
NASA僅使用16位PI數字

Pi的數字有多少位NASA需要對宇宙進行高精度計算嗎?比您想像的要少。
據美國宇航局官員說,航天局很少需要使用超過16位PI(OR 3.141592653589793)對我們的太陽系及其宇宙社區進行準確的計算。根據NASA的數據,使用任何更長的PI版本都會顯著減少回報。
例如:地球的直徑約為7,900英里(12,700公里),這意味著其周長約為24,900英里(40,100公里)。根據NASA的說法,如果您要用PI的前16位數字和更準確的PI計算圓周,則具有數百個小數位的PI,這兩個答案之間的差異將比人毛的寬度少300倍。
該機構補充說,在查看整個宇宙的規模時,PI的較大版本可能很有用。但是,隨著我們太陽系中發生的大多數有趣的空間動作,NASA很少需要大於3.141592653589793。
手動ci

那些希望使用老式技術計算PI的人可以使用標尺,罐子和一根弦,量角器和鉛筆來完成任務。罐方法的缺點是它需要一個實際圓形的罐子,並且精度受到一個人可以在其周圍旋轉的旋轉狀態的限制。同樣,用量角器繪製一個圓,然後用尺子測量其直徑或半徑,涉及相當多的敏捷性和精度。
一個更精確的選擇是使用幾何形狀。將一個圓圈分成多個細分市場(例如八個或10個披薩片)。然後,計算一條直線的長度,該直線將將切片變成一個同等長度的兩個側面三角形。所有側面的加起來可產生PI的粗糙近似值。您創建的切片越多,PI的近似值就越準確。
發現Pi

這古老的巴比倫人知道Pi的存在將近4000年前。公元前1900年至公元前1680年的巴比倫平板電腦將PI計算為3.125,而著名的埃及數學文檔1650年的Rhind數學紙莎草紙列出了3.1605的價值。國王詹姆斯聖經(i Kings 7:23)給出了cubit的pi近似,一個長度的古老單位,對應於前臂的長度從肘部到中指的尖端(估計約為18英寸或46厘米),根據威斯康星大學綠色灣。希臘數學家阿基米德(BC 287-212)使用The Pi近似Pi畢達哥拉斯定理,三角形側面的長度與圓圈內外的多邊形區域之間的幾何關係。
Pi更名

在將符號PI與圓形常數的關聯之前,數學家不得不說一個人甚至可以描述數字。在舊數學書籍中發現的一個短語是拉丁語短語“ Quam cum Multiflicetur直徑,Progeniet carrferencia中的Quantitas”,大致翻譯為“當直徑乘以其乘以其圓周時的數量,而該數量,產生圓周,”根據今天的歷史。
當瑞士多頭性變化時,非理性的數字升起萊昂哈德·歐拉(Leonhard Euler)1737年,他對三角學的駁斥使用了它。但是它並沒有從歐拉(Euler)獲得其pithier,希臘符號的名字。第一次提到PI是在一本鮮為人知的數學家威廉·瓊斯(William Jones)的書中發生的,他在1706年在他的書《 Matholemiorum Matheseos》中使用了它。瓊斯可能會使用PI的符號來表示圈子的外圍,這是“ Pi的歷史”(St. Martin's Press,1976年)。
PI正常嗎?

PI絕對是奇怪的,但是正常嗎?儘管數學家已經掩蓋了這個非理性數字的許多奧秘,但仍然存在一些未解決的問題。
數學家仍然不知道PI是否屬於所謂的正常數字的俱樂部,或數字中所有數字中具有相同頻率的數字 - 這意味著每個時間為0到9,每次出現10%,根據Trueb的網站pi2e.ch。在2016年11月30日發表的論文中預印雜誌Arxiv,TrueB計算出,至少基於前2.24萬億位數字,數字0到9的頻率表明PI是正常的。當然,鑑於PI具有無限數量的數字,因此肯定會證明這一點的唯一方法是創建密封的數學證明。到目前為止,對這個最著名的非理性數字的證明已經避開了科學家,儘管他們在數字的屬性和分佈方面提出了一些範圍。
pi聽起來神聖

儘管科學家不知道PI是否正常,但他們對其其他特徵有更好的了解。十八世紀的數學家約翰·海因里希·蘭伯特(Johann Heinrich Lambert)通過使用持續的部分錶達X的切線,證明了PI的非理性。
後來,數學家表明PI也是超驗。在數學術語中,先驗意味著該數字不能是任何具有合理數量係數的多項式的解決方案。換句話說,沒有有限的根調格公式可以使用有理數來計算PI。
降級PI

儘管許多數學被PI迷上了,但仍有阻力運動。有人認為PI是一個派生的數量,而值TAU(等於PI的兩倍)是一個更直觀的非理性數字。
陶直接將圓周與半徑聯繫起來,這是一個更具數學上的價值,邁克爾·哈特(Michael Hartl)是“ tau宣言”的作者,以前告訴現場科學。 tau在三角計算中也更好地工作,因此tau/4弧度對應於一個掃圈的角度,例如。
PI喜歡聚會

並不總是有PI天(當然,充滿了餡餅)。 1988年,物理學家拉里·肖(Larry Shaw)在總部位於舊金山的探險家科學博物館(Exploratorium Science Museum)推出了PI派對日。每年3月14日(3/14)的工作人員和訪客每年走一場循環遊行(是的,圓形的直徑就像PI乘以其周長),每個人都擁有無限數量的PI。但是直到2009年,眾議院通過了第224號決議,PI Day才成為全國性活動,”支持PI Day的名稱“目標?對數學和科學的興趣增加。讓慶祝活動開始!
編者註:本文的較早版本於2024年3月14日更新,以包括新的更新和信息。現場科學撰稿人Tanya Lewis和編輯Brandon Specktor為本文做出了貢獻。









