9 จำนวนมากที่สุดที่มีอยู่

จำนวนมากมีอยู่ทั่วไปตั้งแต่เซลล์ในร่างกายมนุษย์ไปจนถึงขนาดของจักรวาล แต่เมื่อตัวเลขผ่านขอบเขตของร่างกายของร่างกายจิตใจมนุษย์สามารถดิ้นรนเพื่อเข้าใจถึงขนาดที่ยอดเยี่ยมของตัวเลขเหล่านี้ แม้แต่อินฟินิตี้ก็ดูง่ายกว่าที่จะเข้าใจในการเปรียบเทียบ - มันเพิ่งไปเรื่อย ๆ และเมื่อตัวเลขเริ่มมีขนาดใหญ่พอทุกอย่างก็เริ่มเบลอเข้าด้วยกันจอนบอร์เวนซึ่งเป็นนักคณิตศาสตร์ประยุกต์ที่ University of Newcastle ในออสเตรเลียบอกกับ Live Science ในปี 2013

“ เราไม่เข้าใจตัวเลขในระดับนี้” Borwein กล่าว

จากจำนวนล้านล้านที่ต่ำต้อยถึงหมายเลขของเกรแฮมนี่คือตัวเลขที่เหลือเชื่อที่สุดที่มีอยู่

ใหญ่เป็นญาติ

สิ่งนี้ยังคงมาจากแผนที่การบินผ่านภาพเคลื่อนไหวของแผนที่จักรวาลใหม่ที่สร้างขึ้นโดย Sloan Digital Sky Survey-III แสดงตำแหน่งของกาแลคซีที่แมปในพื้นที่ 3 มิติ(เครดิตภาพ: Miguel A. Aragón (มหาวิทยาลัย Johns Hopkins), Mark Subbarao (Adler Planetarium), Alex Szalay (มหาวิทยาลัย Johns Hopkins), Yushu Yao (Lawrence Berkeley National Laboratory, Nersc) และการร่วมมือ SDSS-III)

เมื่อคิดถึงงบประมาณส่วนบุคคลกเพดานหนี้ $ 31.4 ล้านล้านค่อนข้างนึกไม่ถึง แต่ในระดับของอะตอมในจักรวาลมันดูเล็กมากในการเปรียบเทียบ Scott Aaronson นักวิทยาศาสตร์คอมพิวเตอร์ก่อนหน้านี้ที่ MIT และตอนนี้ที่ University of Texas ที่ Austin บอกกับ Live Science ในปี 2013

ที่เกี่ยวข้อง:ในจักรวาลที่สังเกตได้มีกี่อะตอม?

เพื่อพยายามทำความเข้าใจกับจำนวนมากคนส่วนใหญ่พึ่งพาการเปรียบเทียบขนาด ตัวอย่างเช่น Carl Sagan มีชื่อเสียงในเรื่องอายุของจักรวาลกับปีปฏิทินโดยมนุษย์ปรากฏตัวขึ้นในช่วงสองสามชั่วโมงสุดท้ายของวันส่งท้ายปีเก่า

สมมติฐาน Riemann

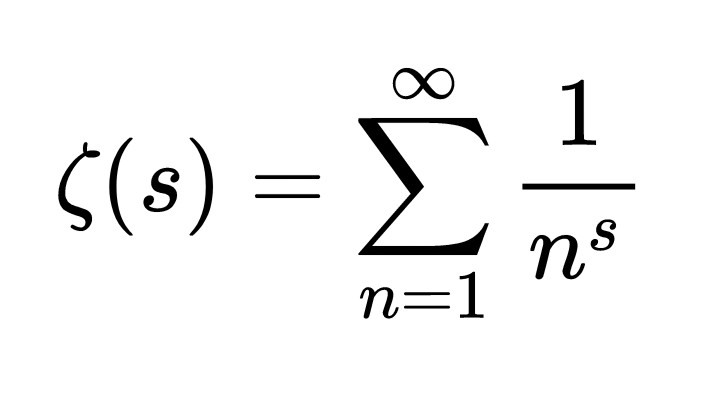
ระบุครั้งแรกในปี 1859สมมติฐานของ Riemannเป็นหนึ่งในการคาดเดาคณิตศาสตร์ที่ยังไม่ได้รับการแก้ไขมากที่สุดและใครก็ตามที่แก้ปัญหาจะได้รับรางวัล 1 ล้านเหรียญ สมมติฐานคือส่วนที่แท้จริงของทุกศูนย์ที่ไม่สำคัญของฟังก์ชั่นเฉพาะชื่อ aptly ชื่อฟังก์ชัน Riemann Zeta คือ 1/2-

“ นี่เป็นคำถามที่เปิดกว้างที่สุดในวิชาคณิตศาสตร์คำถามที่จะรับประกันชื่อของคุณเป็นที่รู้จักใน 10,000 ปี” Borwein กล่าว

สมมติฐานถ้าเป็นจริงมีความหมายที่สำคัญสำหรับการกระจายตัวของจำนวนนายกซึ่งไม่สามารถหารด้วยสิ่งอื่นนอกเหนือจากตัวเองหรือหนึ่ง เพื่อทดสอบสมมติฐานนักคณิตศาสตร์มองหาช่วงเวลาที่มีขนาดใหญ่มาก - ผู้ที่ใหญ่กว่าประมาณ 10 คนที่ยกระดับพลังของ 30 เขากล่าว นั่นอาจฟังดูเป็นนามธรรม แต่มีผลกระทบจากโลกแห่งความเป็นจริงมากมาย Borwein กล่าว “ ช่วงเวลาถูกฝังอยู่ในทุกสิ่งที่เราใช้สำหรับการเข้ารหัส” เขากล่าว "ทั้งหมดนั้นขึ้นอยู่กับสิ่งที่อัลกอริทึมได้รับการออกแบบโดยใช้คุณสมบัติของช่วงเวลาที่เราคิดว่าเป็นจริง แต่ไม่รู้"

จักรวาล

เท่าที่อาร์คิมีดีสนักปรัชญาสงสัยว่าอนุภาคเล็ก ๆ จำนวนเท่าใดจักรวาล- อาร์คิมีสคาดการณ์ว่าประมาณ 10 ถึงพลังของทราย 63 เม็ดสามารถเติมเต็มจักรวาลได้ เขาใช้ชุดของการประมาณที่หยาบมาก - เมล็ดงาดำที่ทำเม็ดทรายเม็ดทรายที่จะครอบคลุมความยาวของสนามกีฬาและความยาวของสตาเดียระหว่างโลกและดวงอาทิตย์กล่าวเฮนรี่เมนเดลนักประวัติศาสตร์คลาสสิกที่ California State University, Los Angeles

แม้จะมีมาตรการดิบเขาก็ไม่ได้อยู่ไกลเกินไป การประมาณการปัจจุบันทำให้จำนวนอะตอมทั้งหมดในจักรวาลอยู่ที่ประมาณ10 ถึง 82-

ปัจจัยด้านจักรวาลวิทยา

Galaxy Cluster Abell 1689 การศึกษาของ Abell 1689 เผยให้เห็นบางสิ่งบางอย่างเกี่ยวกับความมืดที่มีรูปร่างของจักรวาลซึ่งเป็นองค์ประกอบสำคัญของความคลาดเคลื่อนคงที่ทางจักรวาล(เครดิตภาพ: NASA, ESA, E. Jullo (JPL/LAM), P. Natarajan (Yale) และ JP. Kneib (LAM))

เมื่อไอน์สไตน์รู้สึกถึงสมการของเขาสัมพัทธภาพเขารวมค่าคงที่เล็ก ๆ ที่เรียกว่าค่าคงที่ของจักรวาลเพื่ออธิบายถึงความจริงที่ว่าจักรวาลอยู่นิ่ง แม้ว่าเขาจะทิ้งค่าคงที่เมื่อเขาเรียนรู้ว่าจักรวาลกำลังขยายตัว แต่กลับกลายเป็นอัจฉริยะที่อาจเกิดขึ้นกับบางสิ่งบางอย่าง: นักวิทยาศาสตร์เชื่อว่าค่าคงที่ของจักรวาลซึ่งมีเพียง 10 ที่ยกขึ้นสู่อำนาจลบ 122 เผยให้เห็นถึงพลังอันมืดมิด

ค่าคงที่ทางดาราศาสตร์เป็นอาการปวดหัวอย่างมากสำหรับนักวิทยาศาสตร์เนื่องจากการคาดการณ์แตกต่างจากการวัดค่าคงที่โดย 120 คำสั่งขนาดและในช่วงหลายปีที่ผ่านมานักฟิสิกส์ได้พยายามอธิบายความคลาดเคลื่อนนี้โดยการปรับแต่งองค์ประกอบอื่น ๆ เช่นการเปลี่ยนแปลงของมวลอนุภาคตลอดเวลาวิทยาศาสตร์สดรายงานก่อนหน้านี้-

Hercules และ Hydra

ภาพประกอบในศตวรรษที่ 19 ของ Hercules สังหารไฮดรา ตำนานนี้เป็นแรงบันดาลใจให้ปริศนาเกี่ยวกับจำนวนของหัวไฮดราที่จะเพิ่มขึ้นอย่างรวดเร็วหากมีหลายต้นกล้าทุกครั้งที่เฮอร์คิวลิสตัดออก(เครดิตภาพ: Getty Images)

บางครั้งสิ่งต่าง ๆ ต้องใหญ่ขึ้นก่อนที่พวกเขาจะเล็ก ในปี 1982 นักคณิตศาสตร์ Jeff Paris และ Laurie Kirbyวางปริศนาลองนึกภาพ Hercules ต่อสู้กับไฮดราที่เติบโตหัวเหมือนต้นไม้ หากเขาตัดหัวเดียวสัตว์ประหลาดในตำนานก็จะเติบโตขึ้นมาจำนวนหัวที่ถูกควบคุมโดยกฎสองสามข้อ น่าประหลาดใจที่เฮอร์คิวลิสจะเหนือกว่าไฮดราในที่สุดและตัดหัวของไฮดราทั้งหมด

แต่ถึงแม้ว่า Hercules จะฉลาดและเลือกกลยุทธ์ที่มีประสิทธิภาพมากที่สุดไฮดราจะเติบโตมากกว่า googolplex ของหัว (หรือ 10 ยกขึ้นสู่พลังของ 10 ที่เพิ่มขึ้นเป็น 100 พลังงาน)

Mersenne Primes

Marine Mersenne เป็นพระศตวรรษที่ 17 และ Polymath ซึ่งอาจเป็นที่รู้จักกันดีที่สุดในการอธิบายลำดับของจำนวนนายกตอนนี้ตั้งชื่อตามเขา(เครดิตภาพ: Ilbusca/Getty Images)

Mersenne Primes เป็นคลาสของตัวเลขที่ยิ่งใหญ่รีบร้อน ตัวเลขที่สำคัญเหล่านี้เท่ากับ 2 ที่เพิ่มขึ้นสู่พลังของจำนวนที่สำคัญลบด้วย 1 ในขณะที่ไม่กี่คนแรกที่เริ่มต้นเล็ก ๆ น้อย ๆ - 3, 7, 31 - พวกเขาระเบิดขึ้นเพื่อให้มีขนาดใหญ่อย่างไม่น่าเชื่ออย่างรวดเร็ว จนกระทั่งประมาณปี 1951 มีเพียง 12 ของช่วงเวลาเหล่านี้เท่านั้นที่รู้จักกันดี แต่ในปีนี้ (2024) เป็นที่รู้จัก 52

เพื่อเพิ่มพลังให้กับตัวเลขมหึมาเหล่านี้นักวิทยาศาสตร์ใช้การค้นหาอินเทอร์เน็ต Mersenne Primes (GIMPs) ที่ยอดเยี่ยมซึ่งใช้พลังการคำนวณของผู้ใช้อินเทอร์เน็ตหลายพันคนเพื่อค้นหาจำนวนนายกที่เข้าใจยาก ที่หมายเลขสำคัญที่รู้จักมากที่สุดถูกค้นพบในเดือนตุลาคม 2567 โดยนักวิจัยสมัครเล่นและอดีตพนักงานของ Nvidia Luke Durant หมายเลข 2^136,279,841- 1, มีตัวเลข 41,024,320 หลัก, มากกว่า 16 ล้านหลักมากกว่าเจ้าของสถิติก่อนหน้านี้ซึ่งถูกค้นพบโดย GIMPS เมื่อหกปีก่อน

สามล้านล้านสามเหลี่ยม

สามเหลี่ยมที่ถูกต้องซึ่งทั้งสองข้างเป็นจำนวนเต็มหรือเศษส่วนทั้งหมดเป็นที่รู้จักกันในชื่อสามเหลี่ยมที่สอดคล้องกันและพื้นที่ของสามเหลี่ยมดังกล่าวเป็นที่รู้จักกันในชื่อที่สอดคล้องกัน ตัวเลขเหล่านี้อาจมีขนาดใหญ่มากและรวดเร็วมาก(เครดิตภาพ: พื้นหลัง: Eskay Lim / Eyeem ผ่านภาพเก็ตตี้)

ประมาณ 1,000 ปีที่แล้วนักคณิตศาสตร์เปอร์เซียอัลคาราจิครั้งแรกที่ถามว่ามีตัวเลขที่สอดคล้องกันกี่ครั้ง แต่ตัวเลขที่สอดคล้องกันคืออะไร? ตัวเลขเป็นพื้นที่ของสามเหลี่ยมมุมขวาที่มีจำนวนเต็มหรือความยาวเศษส่วน ดังนั้นรูปสามเหลี่ยมที่มีความยาว 3,4 และ 5 จะมีพื้นที่½ * 3 * 4 = 6 ทำให้ 6 เป็นหมายเลขที่สอดคล้องกัน

ต้องใช้เวลานับพันปีก่อนที่จะค้นพบตัวเลขที่สอดคล้องกันร้อยครั้งแรก ภายในปี 2552 อย่างไรก็ตามซูเปอร์คอมพิวเตอร์ได้ค้นพบตัวเลขที่สอดคล้องกัน 3,148,379,694 ครั้งแรก ตัวเลขเหล่านี้บางส่วนมีขนาดใหญ่มากหากตัวเลขของพวกเขาถูกเขียนออกมาในรูปแบบทศนิยมพวกเขาจะยืดออกไปยังดวงจันทร์และกลับ ตัวเลขขนาดมหึมามีความหมายที่น่าสนใจในการจัดเก็บข้อมูลเนื่องจากมีขนาดใหญ่มากจนรังสีแกมมาจรจัดสามารถขัดขวางบิตในตัวเลขเหล่านี้และทำให้พวกเขาผิด Borwein กล่าว

หมายเลขของเกรแฮม

ภาพประกอบนี้แสดงให้เห็นว่าหลุมดำเปล่งออกมาจากพลาสมาที่เคลื่อนที่เร็วด้านบนและด้านล่างดังที่สสารหมุนวนไปรอบ ๆ ในดิสก์ที่โคจรรอบ(เครดิตภาพ: NASA/JPL-CALTECH)

ตัวเลขทั้งหมดเหล่านี้ซีดเมื่อเปรียบเทียบกับหมายเลขของเกรแฮมตัวเลขขนาดใหญ่ที่พยายามจดจำตัวเลขทั้งหมดจะเปลี่ยนหัวของคุณให้กลายเป็นหลุมดำ จำนวนซึ่ง ณ จุดหนึ่งเป็นจำนวนมากที่สุดที่เคยใช้ในการพิสูจน์คณิตศาสตร์เกิดขึ้นเพื่อตอบสนองต่อปริศนาง่ายๆเกี่ยวกับวิธีการจัดสรรผู้คนให้กับคณะกรรมการชุดหนึ่งที่มีข้อ จำกัด เล็กน้อย

ในขณะที่นักคณิตศาสตร์มีความมั่นใจว่าอย่างน้อย 13 คนจำเป็นต้องแก้ปัญหาในปี 1970 นักคณิตศาสตร์และนักเล่นกลโรนัลด์เกรแฮมอนุมานได้ว่าจำนวนคนต้องต่ำกว่าจำนวนของเกรแฮม เพียงแค่คำนวณจำนวนจะใช้เวลา 64 ขั้นตอนและเกี่ยวข้องกับการทวีคูณจำนวน 3s จำนวนมากอย่างบ้าคลั่ง

ไม่มีวิธีที่จะเขียนหมายเลขออกโดยใช้สัญกรณ์ทางวิทยาศาสตร์และต้องเขียนด้วยชุดของ up-arrows ที่แสดงถึงหอคอยของเลขชี้กำลัง ต่อมาเกรแฮมแสดงให้เห็นว่าส่วนบนที่ผูกพันกับปริศนานี้มีขนาดเล็กกว่าจำนวนของเกรแฮมมาก แต่ก็ยังมีขนาดใหญ่มาก

ต้นไม้ (3)

ลำดับของต้นไม้รากที่มีสามฉลาก (สีแดง, เขียวและน้ำเงิน) ต้นไม้ Nth ในลำดับมีจุดยอดมากที่สุดและไม่มีต้นไม้ที่ติดตั้งไว้ภายในต้นไม้ในภายหลังในลำดับ ต้นไม้ (3) ถูกกำหนดให้เป็นความยาวที่ยาวที่สุดเท่าที่จะเป็นไปได้ของลำดับดังกล่าว(เครดิตภาพ: Lightbulbmeow; Wikimedia Commons;(CC BY-SA 4.0)-

ในขณะที่หมายเลขของเกรแฮมเป็นหนึ่งในตัวเลขที่ใหญ่ที่สุดที่เสนอสำหรับการพิสูจน์คณิตศาสตร์ที่เฉพาะเจาะจงนักคณิตศาสตร์ก็ยิ่งใหญ่ขึ้นตั้งแต่นั้นมา ในปี 1998 นักตรรกฮาร์วีย์ฟรีดแมนของมหาวิทยาลัยรัฐโอไฮโอเสนอปริศนาการถามว่าต้องมีลำดับตัวอักษรนานเท่าใดที่ต้องได้รับพารามิเตอร์บางอย่างของการยืดตัวอักษรซ้ำ ในขณะที่คำตอบนั้นไม่สิ้นสุด แต่ก็มีขนาดใหญ่มาก

จำนวน Friedman ที่ได้มาจากต้นไม้ (3) คำนวณโดยการสร้างหอคอยขนาดใหญ่ที่เพิ่มขึ้นของ Twos ขึ้นสู่พลังของสองสิ่งที่ใช้สิ่งที่เรียกว่าฟังก์ชั่น Ackerman เพื่อให้ความรู้สึกของสเกลฟังก์ชั่น Ackerman ที่สี่เกี่ยวข้องกับการเพิ่มพลังสองถึง 65,536 Twos แต่ต้นไม้ (3) มีขนาดใหญ่กว่าขนาดใหญ่ - ใหญ่มากจนทำให้จำนวนของเกรแฮมดูเหมือนฝุ่นที่เล็กที่สุดในการเปรียบเทียบ

“ ระดับที่สูงขึ้นของความเบลอที่สูงขึ้นซึ่งไม่สามารถสัมผัสได้ถึงระดับหนึ่งของความใหญ่โตจากอีกระดับหนึ่ง” ฟรีดแมนเขียนไว้ในบทความของเขา

หมายเหตุบรรณาธิการ: บทความนี้ได้รับการตีพิมพ์ครั้งแรกในปี 2013 และอัปเดตเมื่อวันที่ 17 พฤศจิกายน 2566 เพื่อจดบันทึกข้อมูลใหม่เกี่ยวกับนายกที่ใหญ่ที่สุดอะตอมในจักรวาลที่สังเกตได้และค่าคงที่จักรวาล บทความได้รับการอัปเดตอีกครั้งในเดือนตุลาคม 2567 หลังจากค้นพบจำนวนนายกที่ใหญ่ที่สุดใหม่

รับการค้นพบที่น่าสนใจที่สุดในโลกที่ส่งตรงไปยังกล่องจดหมายของคุณ