ทีมของนักคณิตศาสตร์เพียงแค่ก้าวสำคัญในการตอบคำถามอายุ 160 ปีล้านดอลลาร์ในวิชาคณิตศาสตร์?
อาจจะ. ลูกเรือได้แก้ปัญหาคำถามอื่น ๆ อีกจำนวนหนึ่งในสาขาที่เรียกว่าจำนวนทฤษฎีจำนวน และในการทำเช่นนั้นพวกเขาได้เปิดถนนเก่าอีกครั้งซึ่งในที่สุดอาจนำไปสู่คำตอบสำหรับคำถามเก่า ๆ : คือสมมติฐาน Riemannถูกต้อง?
สมมติฐาน Reimann เป็นการคาดเดาทางคณิตศาสตร์ขั้นพื้นฐานที่มีความหมายอย่างมากสำหรับส่วนที่เหลือของคณิตศาสตร์ มันเป็นรากฐานสำหรับความคิดทางคณิตศาสตร์อื่น ๆ อีกมากมาย - แต่ไม่มีใครรู้ว่ามันเป็นเรื่องจริงหรือไม่ ความถูกต้องของมันได้กลายเป็นหนึ่งในคำถามเปิดที่มีชื่อเสียงที่สุดในวิชาคณิตศาสตร์ มันเป็นหนึ่งในเจ็ด "ปัญหาสหัสวรรษ"วางไว้ในปี 2000 ด้วยสัญญาว่าใครก็ตามที่แก้ปัญหาพวกเขาจะชนะ $ 1 ล้าน (มีเพียงปัญหาเดียวเท่านั้นที่ได้รับการแก้ไข) [5 ข้อเท็จจริงทางคณิตศาสตร์ที่เหลือเชื่ออย่างจริงจัง-
ความคิดนี้มาจากไหน?
ย้อนกลับไปในปี 1859 นักคณิตศาสตร์ชาวเยอรมันชื่อ Bernhard Riemann เสนอคำตอบสำหรับสมการคณิตศาสตร์ที่มีหนามโดยเฉพาะ สมมติฐานของเขาเป็นเช่นนี้: ส่วนที่แท้จริงของทุกศูนย์ที่ไม่สำคัญของฟังก์ชั่น Riemann Zeta คือ 1/2-นั่นเป็นเรื่องสวยคำสั่งทางคณิตศาสตร์บทคัดย่อต้องทำกับตัวเลขที่คุณสามารถใส่ลงในฟังก์ชันทางคณิตศาสตร์เฉพาะเพื่อให้ฟังก์ชั่นนั้นเท่ากันศูนย์ แต่มันกลับกลายเป็นว่ามีความสำคัญมากที่สุดเกี่ยวกับคำถามเกี่ยวกับความถี่ที่คุณจะพบจำนวนนายกในขณะที่คุณนับรวมถึงอินฟินิตี้
เราจะกลับมาที่รายละเอียดของสมมติฐานในภายหลัง แต่สิ่งสำคัญที่ต้องรู้ตอนนี้คือถ้าสมมติฐานของ Riemann เป็นความจริงมันจะตอบคำถามมากมายในวิชาคณิตศาสตร์
"บ่อยครั้งในทฤษฎีจำนวนสิ่งที่เกิดขึ้นคือถ้าคุณคิดว่าสมมติฐานของ Riemann [เป็นจริง] คุณสามารถพิสูจน์ผลลัพธ์อื่น ๆ ได้ทุกชนิด" Lola Thompson นักทฤษฎีจำนวนหนึ่งที่ Oberlin College ในโอไฮโอซึ่งไม่ได้เกี่ยวข้องกับการวิจัยล่าสุดนี้กล่าว
บ่อยครั้งที่เธอบอกกับ Live Science นักทฤษฎีจำนวนจะพิสูจน์ก่อนว่ามีบางอย่างเป็นจริงถ้าสมมติฐานของ Riemann เป็นจริง จากนั้นพวกเขาจะใช้หลักฐานนั้นเป็นประเภทของหินก้าวไปสู่หลักฐานที่ซับซ้อนมากขึ้นซึ่งแสดงให้เห็นว่าข้อสรุปดั้งเดิมของพวกเขาเป็นจริงไม่ว่าสมมติฐานของ Riemann จะเป็นจริงหรือไม่
ความจริงที่ว่าเคล็ดลับนี้เธอพูดว่าทำงานได้โน้มน้าวนักคณิตศาสตร์หลายคนว่าสมมติฐานของ Riemann ต้องเป็นจริง
แต่ความจริงก็คือไม่มีใครรู้แน่นอน
ก้าวเล็ก ๆ ไปสู่การพิสูจน์?
ดังนั้นทีมนักคณิตศาสตร์ขนาดเล็กนี้ดูเหมือนจะนำเราเข้าใกล้ทางออกมากขึ้น?
“ สิ่งที่เราทำในบทความของเรา” เคนโอโน่นักทฤษฎีจำนวนหนึ่งของมหาวิทยาลัยเอมอรีและผู้เขียนร่วมของหลักฐานใหม่กล่าว“ เราได้กลับมาอีกครั้งเกณฑ์ทางเทคนิคมากซึ่งเทียบเท่ากับสมมติฐาน Riemann …และเราได้พิสูจน์ส่วนใหญ่ของมัน
"เกณฑ์ที่เทียบเท่ากับสมมติฐานของ Riemann" ในกรณีนี้หมายถึงคำแถลงแยกต่างหากที่เทียบเท่าทางคณิตศาสตร์กับสมมติฐานของ Riemann
ไม่ชัดเจนในตอนแรกว่าทำไมทั้งสองข้อความถึงเชื่อมต่อกัน (เกณฑ์เกี่ยวข้องกับสิ่งที่เรียกว่า "ความดันโลหิตสูงของพหุนามเจนเซ่น") แต่ในปี 1920 นักคณิตศาสตร์ชาวฮังการีชื่อจอร์จพอฟลิยาพิสูจน์ว่าถ้าเกณฑ์นี้เป็นจริง มันเป็นเส้นทางเก่าที่เสนอไปสู่การพิสูจน์สมมติฐาน แต่เส้นทางที่ถูกทอดทิ้งเป็นส่วนใหญ่
Ono และเพื่อนร่วมงานของเขาในบทความที่ตีพิมพ์เมื่อวันที่ 21 พฤษภาคมในวารสารการดำเนินการของ Natural Academy of Sciences(PNAs) พิสูจน์แล้วว่าในหลาย ๆ กรณีหลายกรณีเกณฑ์เป็นจริง
แต่ในวิชาคณิตศาสตร์หลายคนไม่เพียงพอที่จะนับเป็นข้อพิสูจน์ ยังมีบางกรณีที่พวกเขาไม่รู้ว่าเกณฑ์เป็นจริงหรือเท็จ
“ มันเหมือนกับการเล่น Powerball จำนวนล้านครั้ง” Ono กล่าว "และคุณรู้ตัวเลขทั้งหมด แต่ 20 คนสุดท้ายถ้าแม้แต่หนึ่งใน 20 หมายเลขสุดท้ายก็ผิดคุณก็แพ้ ... มันอาจจะล้มลงทั้งหมด"
นักวิจัยจะต้องมีหลักฐานขั้นสูงมากขึ้นเพื่อแสดงให้เห็นว่าเกณฑ์นั้นเป็นจริงในทุกกรณีดังนั้นจึงพิสูจน์สมมติฐานของ Riemann และยังไม่ชัดเจนว่าการพิสูจน์ดังกล่าวอยู่ไกลแค่ไหน Ono กล่าว
แล้วบทความนี้มีข้อตกลงขนาดใหญ่แค่ไหน?
ในแง่ของสมมติฐานของ Riemann มันยากที่จะบอกว่าข้อตกลงนี้ใหญ่แค่ไหน มากขึ้นอยู่กับสิ่งที่เกิดขึ้นต่อไป
“ [เกณฑ์] นี้เป็นเพียงหนึ่งในหลายสูตรที่เทียบเท่าของสมมติฐาน Riemann” ธ อมป์สันกล่าว
กล่าวอีกนัยหนึ่งมีความคิดอื่น ๆ อีกมากมายที่เช่นเกณฑ์นี้จะพิสูจน์ได้ว่าสมมติฐานของ Riemann นั้นเป็นจริงหากพวกเขาเองได้รับการพิสูจน์แล้ว-
“ ดังนั้นจึงยากที่จะรู้ว่ามันมีความคืบหน้ามากแค่ไหนเพราะในอีกด้านหนึ่งมันมีความคืบหน้าในทิศทางนี้ แต่มีสูตรที่เทียบเท่ากันมากมายซึ่งบางทีทิศทางนี้อาจไม่ได้รับสมมติฐาน Riemann
หากหลักฐานปรากฏขึ้นตามเส้นทางนี้นั่นอาจหมายถึง Ono และเพื่อนร่วมงานของเขาได้พัฒนากรอบพื้นฐานที่สำคัญสำหรับการแก้สมมติฐาน Riemann แต่ถ้ามันปรากฏขึ้นที่อื่นบทความนี้จะกลายเป็นสิ่งสำคัญน้อยกว่า
ถึงกระนั้นนักคณิตศาสตร์ก็ประทับใจ
“ แม้ว่าสิ่งนี้จะยังห่างไกลจากการพิสูจน์สมมติฐานของ Riemann มันเป็นก้าวสำคัญ” Encrico Bombieri นักทฤษฎีหมายเลขพรินซ์ตันที่ไม่ได้มีส่วนร่วมในการวิจัยของทีมเขียนในวันที่ 23 พฤษภาคมที่ผ่านมาPNAsบทความ. "ไม่ต้องสงสัยเลยว่าบทความนี้จะสร้างแรงบันดาลใจให้กับงานพื้นฐานเพิ่มเติมในด้านทฤษฎีจำนวนมากเช่นเดียวกับในฟิสิกส์ทางคณิตศาสตร์"
(Bombieriได้รับรางวัลเหรียญ- รางวัลที่มีชื่อเสียงที่สุดในวิชาคณิตศาสตร์ - ในปี 1974 ส่วนใหญ่สำหรับงานที่เกี่ยวข้องกับสมมติฐานของ Riemann)
สมมติฐานของ Riemann หมายถึงอะไร?
ฉันสัญญาว่าเราจะกลับมาที่นี่ นี่คือสมมติฐานของ Riemann อีกครั้ง: ส่วนที่แท้จริงของฟังก์ชั่น Riemann Zeta ทุกอย่างที่ไม่สำคัญคือ 1/2-
มาทำลายมันลงไปตามวิธีที่ Thompson และ Ono อธิบาย
ก่อนอื่นฟังก์ชั่น Riemann Zeta คืออะไร?
ในวิชาคณิตศาสตร์ฟังก์ชั่นคือความสัมพันธ์ระหว่างปริมาณทางคณิตศาสตร์ที่แตกต่างกัน คนง่าย ๆ อาจมีลักษณะเช่นนี้: y = 2x
ฟังก์ชั่น Riemann Zeta เป็นไปตามหลักการพื้นฐานเดียวกัน มีเพียงมันซับซ้อนกว่ามาก นี่คือสิ่งที่ดูเหมือน
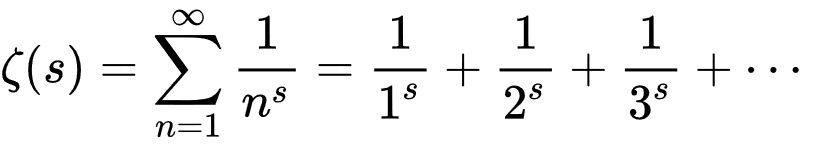
มันเป็นผลรวมของไฟล์ไม่มีที่สิ้นสุดลำดับโดยที่แต่ละเทอม - สองสามตัวแรกคือ 1/1^s, 1/2^s และ 1/3^s - ถูกเพิ่มเข้าไปในข้อกำหนดก่อนหน้า จุดไข่ปลาเหล่านั้นหมายถึงซีรีส์ในฟังก์ชั่นยังคงดำเนินต่อไปเช่นนั้นตลอดไป
ตอนนี้เราสามารถตอบคำถามที่สอง: ฟังก์ชั่น Riemann Zeta เป็นศูนย์คืออะไร?
ง่ายกว่า "ศูนย์" ของฟังก์ชั่นคือหมายเลขใด ๆ ที่คุณสามารถใส่สำหรับ x ซึ่งทำให้ฟังก์ชันเท่ากับศูนย์
คำถามต่อไป: "ส่วนจริง" ของหนึ่งในศูนย์เหล่านั้นคืออะไรและหมายความว่าอะไรเท่ากับ 1/2?
ฟังก์ชั่น Riemann Zeta เกี่ยวข้องกับสิ่งที่นักคณิตศาสตร์เรียกว่า "ตัวเลขที่ซับซ้อน. "ตัวเลขที่ซับซ้อนดูเหมือนว่า: A+B*i
ในสมการนั้น "A" และ "B" หมายถึงจำนวนจริงใด ๆ จำนวนจริงสามารถเป็นอะไรก็ได้ตั้งแต่ลบ 3 ถึงศูนย์ถึง 4.9234PIหรือ 1 พันล้าน แต่มีหมายเลขอื่น:ตัวเลขจินตภาพ- ตัวเลขจินตภาพเกิดขึ้นเมื่อคุณใช้รากที่สองของจำนวนลบและพวกเขามีความสำคัญปรากฏขึ้นในบริบททางคณิตศาสตร์ทุกชนิด -10 ข้อเท็จจริงที่น่าประหลาดใจเกี่ยวกับ PI-
จำนวนจินตนาการที่ง่ายที่สุดคือสแควร์รูทของ -1 ซึ่งเขียนเป็น "i." หมายเลขที่ซับซ้อนคือจำนวนจริง ("A") บวกกับจำนวนจริงอีกครั้ง ("B") ครั้งที่ฉัน "ส่วนจริง" ของหมายเลขที่ซับซ้อนคือ "ก."
ศูนย์ไม่กี่ของฟังก์ชั่น Riemann Zeta จำนวนเต็มลบระหว่าง -10 ถึง 0 อย่านับสำหรับสมมติฐานของ Reimann สิ่งเหล่านี้ถือเป็นศูนย์ "เล็กน้อย" เพราะเป็นตัวเลขจริงไม่ใช่ตัวเลขที่ซับซ้อน ศูนย์อื่น ๆ ทั้งหมดคือ "ไม่สำคัญ" และตัวเลขที่ซับซ้อน
สมมติฐานของ Riemann ระบุว่าเมื่อฟังก์ชัน Riemann Zeta ข้ามศูนย์ (ยกเว้นศูนย์เหล่านั้นระหว่าง -10 และ 0) ส่วนที่แท้จริงของหมายเลขที่ซับซ้อนจะต้องเท่ากับ 1/2
การอ้างสิทธิ์เล็กน้อยนั้นอาจไม่สำคัญมาก แต่มันคือ. และเราอาจจะเป็นเพียงแค่การแก้ปัญหาเล็ก ๆ น้อย ๆ
เผยแพร่ครั้งแรกเมื่อวิทยาศาสตร์สด-