สมการทางคณิตศาสตร์นำเสนอหน้าต่างที่ไม่เหมือนใครในโลก พวกเขาเข้าใจถึงความเป็นจริงและช่วยให้เราเห็นสิ่งที่ไม่เคยสังเกตมาก่อน ดังนั้นจึงไม่น่าแปลกใจที่การพัฒนาใหม่ในวิชาคณิตศาสตร์มักจะจับมือกับความก้าวหน้าในการทำความเข้าใจจักรวาลของเรา ที่นี่เรามาดูสมการเก้าจากประวัติศาสตร์ที่ปฏิวัติวิธีที่เรามองทุกอย่างตั้งแต่อนุภาคเล็ก ๆ ไปจนถึงจักรวาลอันกว้างใหญ่
ทฤษฎีบทพีทาโกรัส
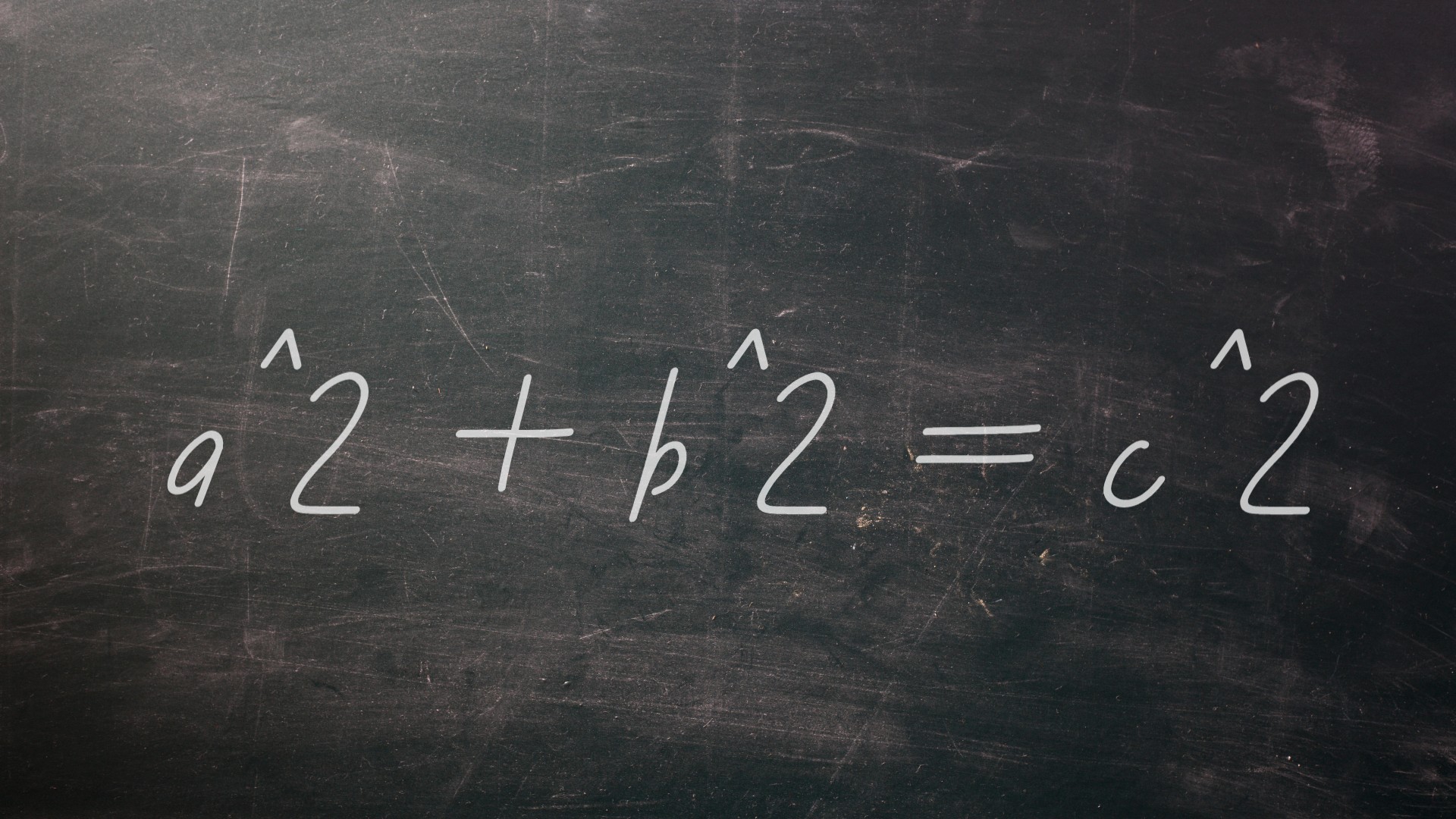
หนึ่งในวิชาเอกแรกตรีโกณมิติกฎที่ผู้คนเรียนรู้ในโรงเรียนคือความสัมพันธ์ระหว่างด้านข้างของสามเหลี่ยมด้านขวา: ความยาวของแต่ละด้านที่สั้นกว่าสองด้านกำลังสองและเพิ่มเข้าด้วยกันเท่ากับความยาวของด้านที่ยาวที่สุดกำลังสอง โดยปกติจะเขียนเป็น^2 + b^2 = c^2 และมันได้รับเป็นที่รู้จักอย่างน้อย 3,700 ปีตั้งแต่ช่วงเวลาของชาวบาบิโลนโบราณ
นักคณิตศาสตร์ชาวกรีกนักคณิตศาสตร์มหาวิทยาลัยเซนต์แอนดรูในสกอตแลนด์ นอกเหนือจากการค้นหาการใช้งานในการก่อสร้างการนำทางการทำแผนที่และกระบวนการสำคัญอื่น ๆ ทฤษฎีบทพีทาโกรัสช่วยขยายแนวคิดของตัวเลข ในศตวรรษที่ห้าก่อนคริสต์ศักราชนักคณิตศาสตร์ Hippasus ของ metapontum สังเกตเห็นว่าสามเหลี่ยมจกรนติที่มีด้านขวาซึ่งสองด้านฐานมีความยาว 1 หน่วยจะมี hypotenuse นั่นคือรากที่สองของ 2 ซึ่งเป็นจำนวนไม่มีเหตุผล- (จนกระทั่งถึงจุดนั้นไม่มีใครในประวัติศาสตร์ที่บันทึกไว้ได้พบตัวเลขดังกล่าว) สำหรับการค้นพบของเขาฮิปโปซัสได้รับการกล่าวขานว่าถูกโยนลงไปในทะเลเพราะผู้ติดตามของพีธากอรัส (รวมถึงฮิปโปซัส) ถูกรบกวนจากความเป็นไปได้ของตัวเลขที่เกิดขึ้นตลอดไปตามบทความจากมหาวิทยาลัยเคมบริดจ์
f = ma และกฎแห่งแรงโน้มถ่วง
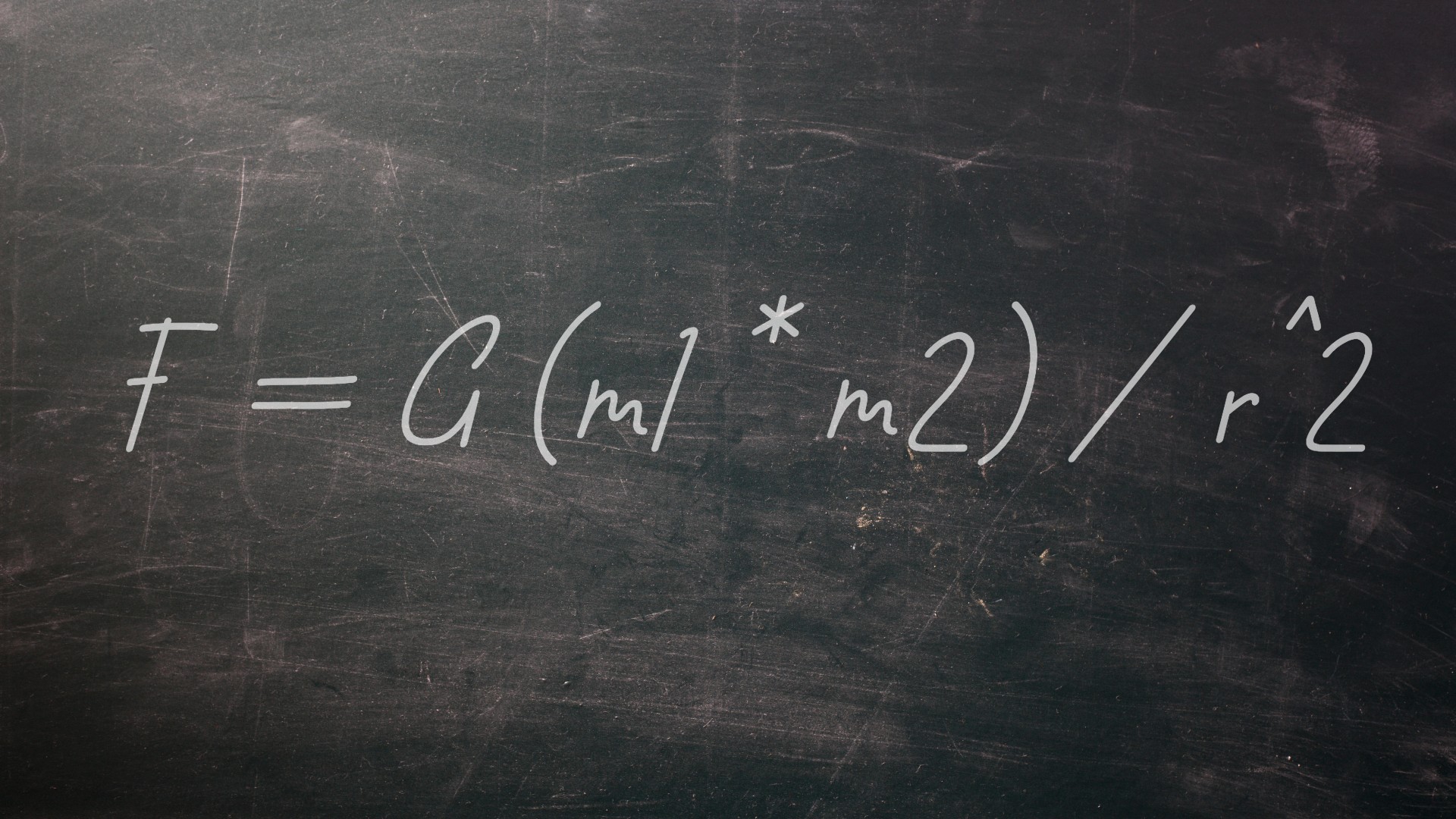
Sir Isaac Newton ของอังกฤษได้รับการยกย่องด้วยจำนวนมากผลการค้นพบของโลก- ในหมู่พวกเขาคือเขากฎข้อที่สองของการเคลื่อนไหวซึ่งระบุว่าแรงเท่ากับมวลของวัตถุเวลาการเร่งความเร็วของมันมักจะเขียนเป็น f = ma ส่วนขยายของกฎหมายนี้รวมกับการสังเกตอื่น ๆ ของนิวตันทำให้เขาในปี 1687 เพื่ออธิบายสิ่งที่เรียกว่ากฎของเขาในขณะนี้แรงโน้มถ่วงสากล- มันมักจะเขียนเป็น f = g (m1 * m2) / r^2 โดยที่ m1 และ m2 เป็นมวลของวัตถุสองวัตถุและ r คือระยะห่างระหว่างพวกเขา G เป็นค่าคงที่พื้นฐานที่จะต้องค้นพบค่าผ่านการทดลอง แนวคิดเหล่านี้ถูกนำมาใช้เพื่อทำความเข้าใจระบบทางกายภาพมากมายตั้งแต่รวมถึงการเคลื่อนที่ของดาวเคราะห์ในระบบสุริยจักรวาลและวิธีการเดินทางระหว่างพวกเขาโดยใช้จรวด
สมการคลื่น
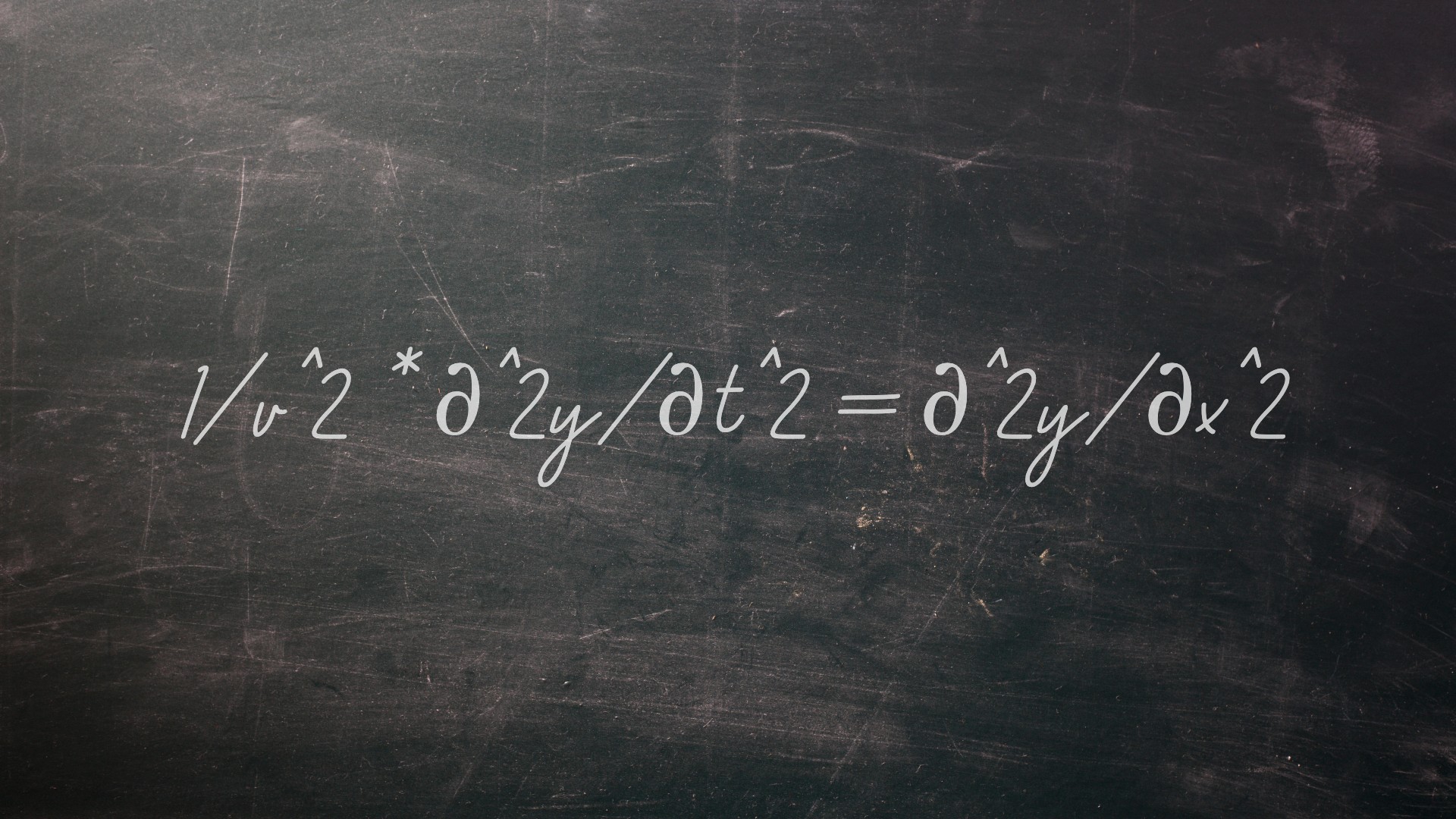
ด้วยการใช้กฎหมายใหม่ของนิวตันนักวิทยาศาสตร์ในศตวรรษที่ 18 เริ่มวิเคราะห์ทุกสิ่งรอบตัวพวกเขา ในปี ค.ศ. 1743 Jean-Baptiste Le Rond D'Alembert ฝรั่งเศสได้รับสมการที่อธิบายถึงการสั่นสะเทือนของสายการสั่นหรือการเคลื่อนไหวของคลื่นตามรายงานที่ตีพิมพ์ในปี 2020 ในวารสารความก้าวหน้าในการศึกษาประวัติศาสตร์- สมการสามารถเขียนได้ดังนี้:
1/v^2 * ∂^2y/∂t^2 = ∂^2y/∂x^2
ในสมการนี้ V คือความเร็วของคลื่นและส่วนอื่น ๆ อธิบายการกระจัดของคลื่นในทิศทางเดียว ขยายไปถึงสองมิติหรือมากกว่าสมการคลื่นช่วยให้นักวิจัยสามารถทำนายการเคลื่อนไหวของน้ำคลื่นไหวสะเทือนและเสียงและเป็นพื้นฐานสำหรับสิ่งต่าง ๆ เช่นสมการSchrödingerฟิสิกส์ควอนตัมซึ่งเป็นรากฐานของอุปกรณ์คอมพิวเตอร์ที่ทันสมัยจำนวนมาก
สมการของฟูริเยร์
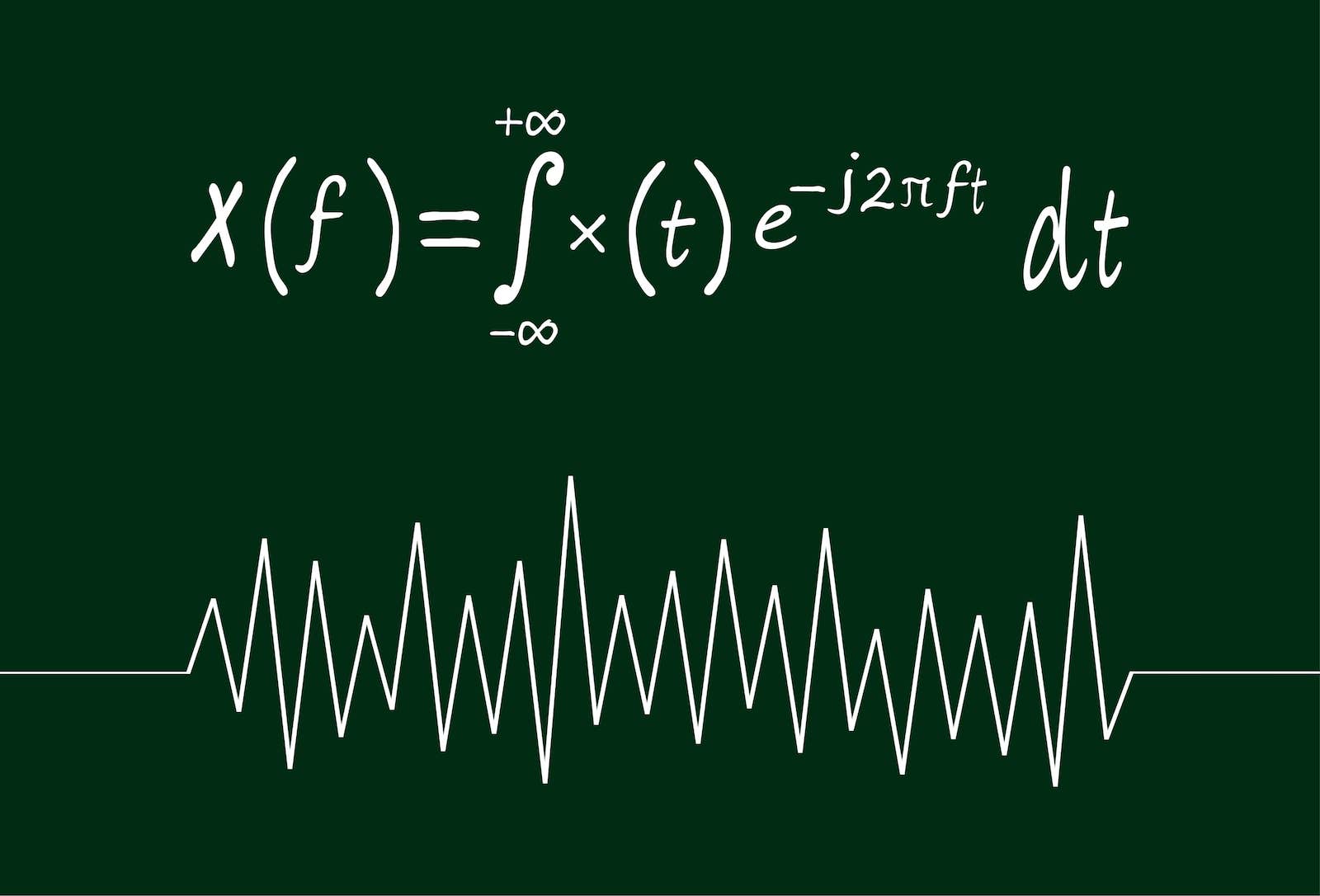
แม้ว่าคุณจะยังไม่เคยได้ยินเรื่อง Baron Jean-Baptiste Joseph Joseph Fourier งานของเขาก็ส่งผลกระทบต่อชีวิตของคุณ นั่นเป็นเพราะสมการทางคณิตศาสตร์ที่เขาเขียนลงในปี 1822 ได้อนุญาตให้นักวิจัยทำลายข้อมูลที่ซับซ้อนและยุ่งเหยิงในการรวมกันของคลื่นง่าย ๆ ที่ง่ายต่อการวิเคราะห์ การแปลงฟูริเยร์ตามที่ทราบกันดีว่าเป็นความคิดที่รุนแรงในเวลานั้นโดยนักวิทยาศาสตร์หลายคนปฏิเสธที่จะเชื่อว่าระบบที่ซับซ้อนสามารถลดลงไปสู่ความเรียบง่ายที่สง่างามเช่นนี้ตามบทความในบทความYale Scientific- แต่การแปลงฟูริเยร์เป็นงานที่ทำงานในสาขาวิทยาศาสตร์สมัยใหม่หลายแห่งรวมถึงการประมวลผลข้อมูลการวิเคราะห์ภาพเลนส์การสื่อสารดาราศาสตร์และวิศวกรรม
สมการของ Maxwell
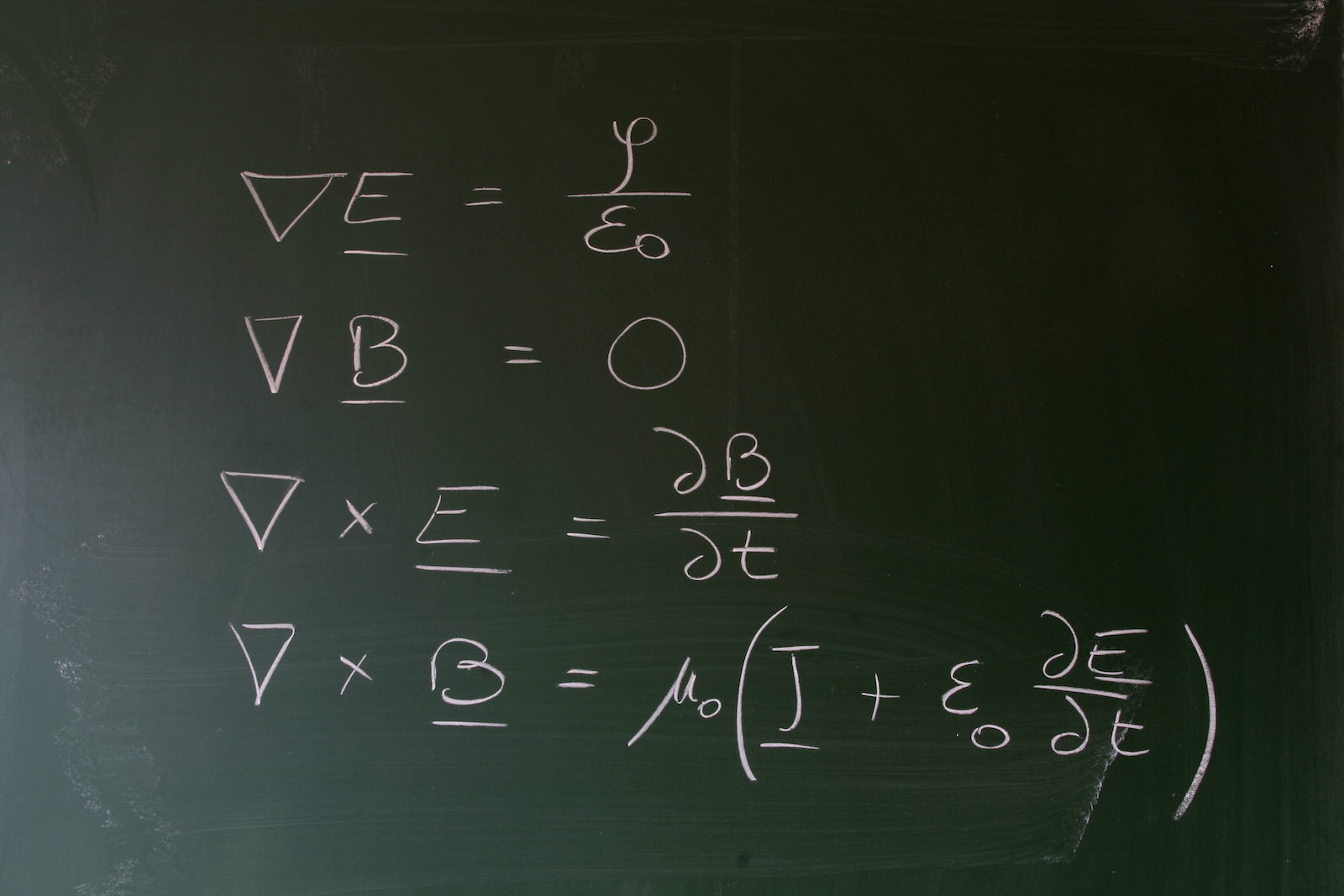
ไฟฟ้าและแม่เหล็กยังคงเป็นแนวคิดใหม่ในปี 1800 เมื่อนักวิชาการตรวจสอบวิธีการจับและควบคุมกองกำลังแปลก ๆ เหล่านี้ นักวิทยาศาสตร์ชาวสก็อตJames Clerk Maxwellเพิ่มความเข้าใจของเราอย่างมากเกี่ยวกับปรากฏการณ์ทั้งสองในปี 2407 เมื่อเขาตีพิมพ์รายการสมการ 20 สมการที่อธิบายว่าไฟฟ้าและแม่เหล็กทำงานได้อย่างไรและมีความสัมพันธ์กันอย่างไร ต่อมาได้รับการฝึกฝนให้กับสี่ตอนนี้สมการของแมกซ์เวลล์ได้รับการสอนให้กับนักศึกษาฟิสิกส์ปีแรกในวิทยาลัยและเป็นพื้นฐานสำหรับทุกสิ่งอิเล็กทรอนิกส์ในโลกเทคโนโลยีที่ทันสมัยของเรา
e = mc^2
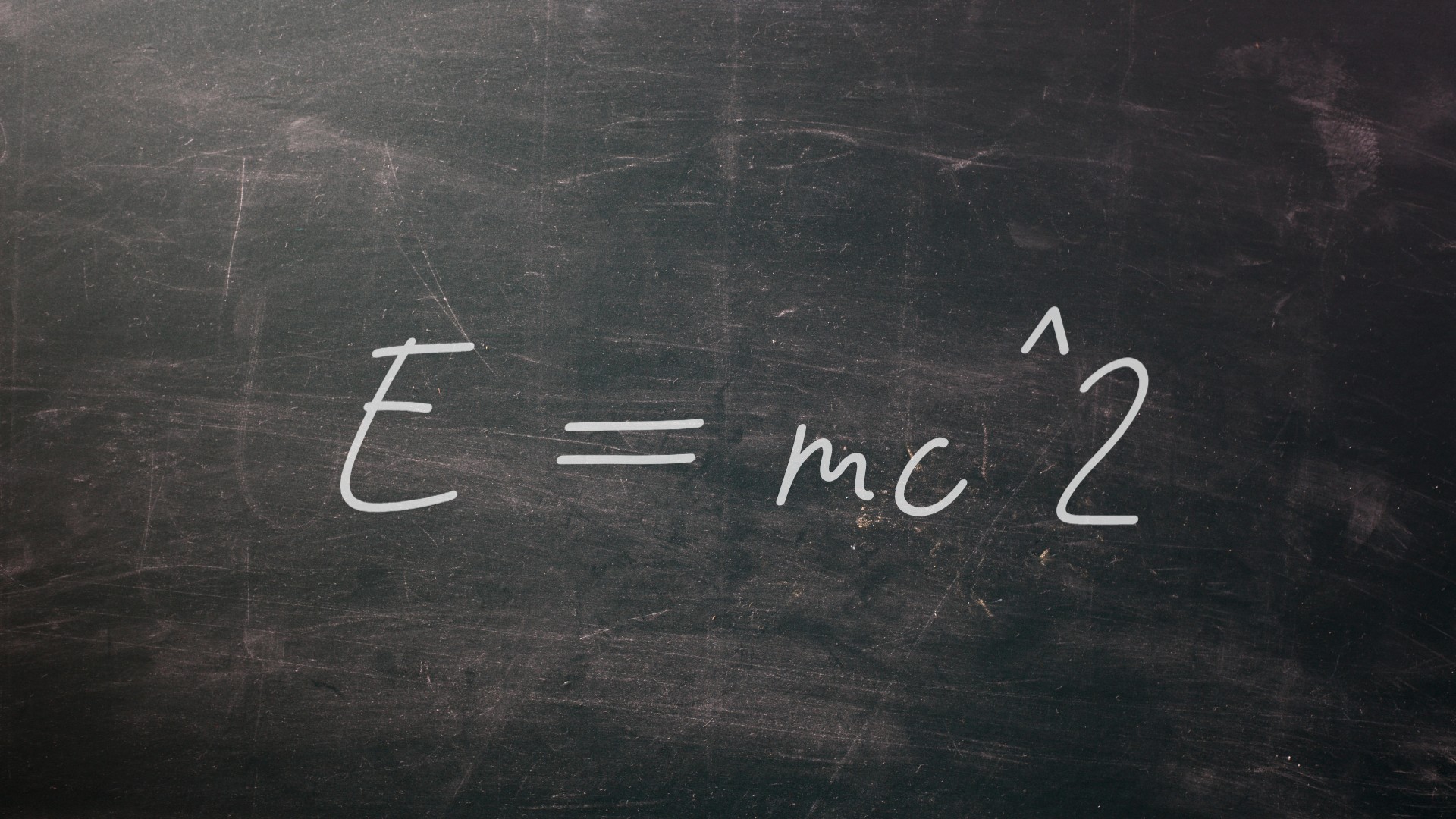
ไม่มีรายการสมการการเปลี่ยนแปลงที่จะเสร็จสมบูรณ์หากไม่มีสมการที่มีชื่อเสียงที่สุดของทั้งหมด ระบุครั้งแรกโดยอัลเบิร์ตไอน์สไตน์ในปี 1905 ซึ่งเป็นส่วนหนึ่งของทฤษฎีสัมพัทธภาพพิเศษของเขาe = mc^2แสดงให้เห็นว่าเรื่องและพลังงานเป็นสองด้านของสิ่งหนึ่ง ในสมการ E หมายถึงพลังงาน M หมายถึงมวลและ C คือความเร็วคงที่ของแสง แนวคิดที่มีอยู่ในคำแถลงง่ายๆนั้นยังคงยากสำหรับหลาย ๆ คนที่จะห่อหุ้มจิตใจของพวกเขา แต่หากไม่มี e = mc^2 เราจะไม่เข้าใจว่าดาวหรือจักรวาลทำงานอย่างไรหรือรู้ว่าจะสร้างตัวเร่งอนุภาคขนาดมหึมาเช่นHadron Collider ขนาดใหญ่เพื่อตรวจสอบธรรมชาติของโลก subatomic
สมการของ Friedmann
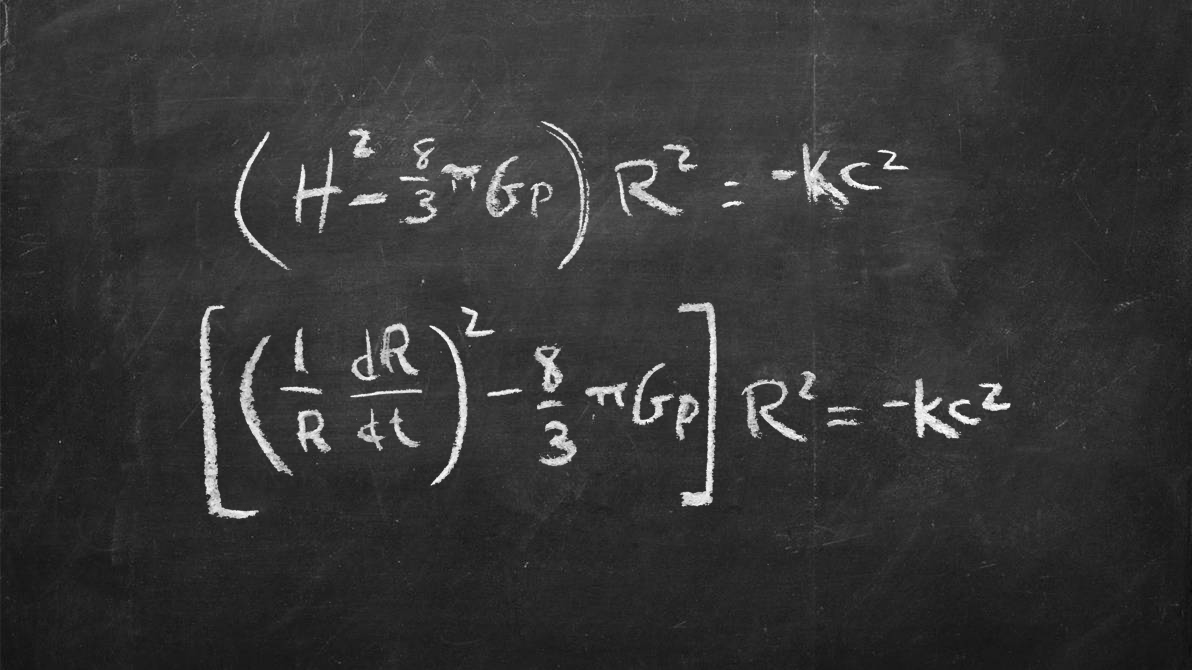
ดูเหมือนว่าจะโอ้อวดที่จะคิดว่าคุณสามารถสร้างชุดของสมการที่กำหนดจักรวาลทั้งหมด แต่นั่นเป็นสิ่งที่นักฟิสิกส์รัสเซียอเล็กซานเดอร์ฟรีดแมนน์ทำในปี 1920 การใช้ทฤษฎีสัมพัทธภาพของไอน์สไตน์ Freidmann แสดงให้เห็นว่าลักษณะของจักรวาลที่กำลังขยายตัวสามารถแสดงออกได้จากบิ๊กแบงเป็นต้นไปโดยใช้สมการสองสมการ
พวกเขารวมแง่มุมที่สำคัญทั้งหมดของจักรวาลรวมถึงความโค้งของมันสสารและพลังงานที่มีอยู่เท่าไหร่และการขยายตัวเร็วแค่ไหนรวมถึงค่าคงที่สำคัญจำนวนมากเช่นความเร็วของแสงค่าคงที่แรงโน้มถ่วงและค่าคงที่ฮับเบิลซึ่งรวบรวมการขยายตัวของจักรวาล ไอน์สไตน์มีชื่อเสียงไม่ชอบความคิดของจักรวาลที่กำลังขยายตัวหรือหดตัวซึ่งทฤษฎีสัมพัทธภาพทั่วไปของเขาแนะนำจะเกิดขึ้นเนื่องจากผลกระทบของแรงโน้มถ่วง เขาพยายามเพิ่มตัวแปรในผลลัพธ์ที่แสดงโดยแลมบ์ดาตัวอักษรกรีกที่ทำหน้าที่ตอบโต้กับแรงโน้มถ่วงเพื่อทำให้จักรวาลคงที่ ในขณะที่เขาเรียกมันว่าความผิดพลาดที่ยิ่งใหญ่ที่สุดของเขาหลายทศวรรษหลังจากนั้นความคิดก็ถูกปัดฝุ่นออกไปและแสดงให้เห็นว่ามีอยู่ในรูปแบบของสารลึกลับพลังงานมืดซึ่งกำลังผลักดันการขยายตัวของจักรวาลอย่างเร่งด่วน
สมการข้อมูลของแชนนอน
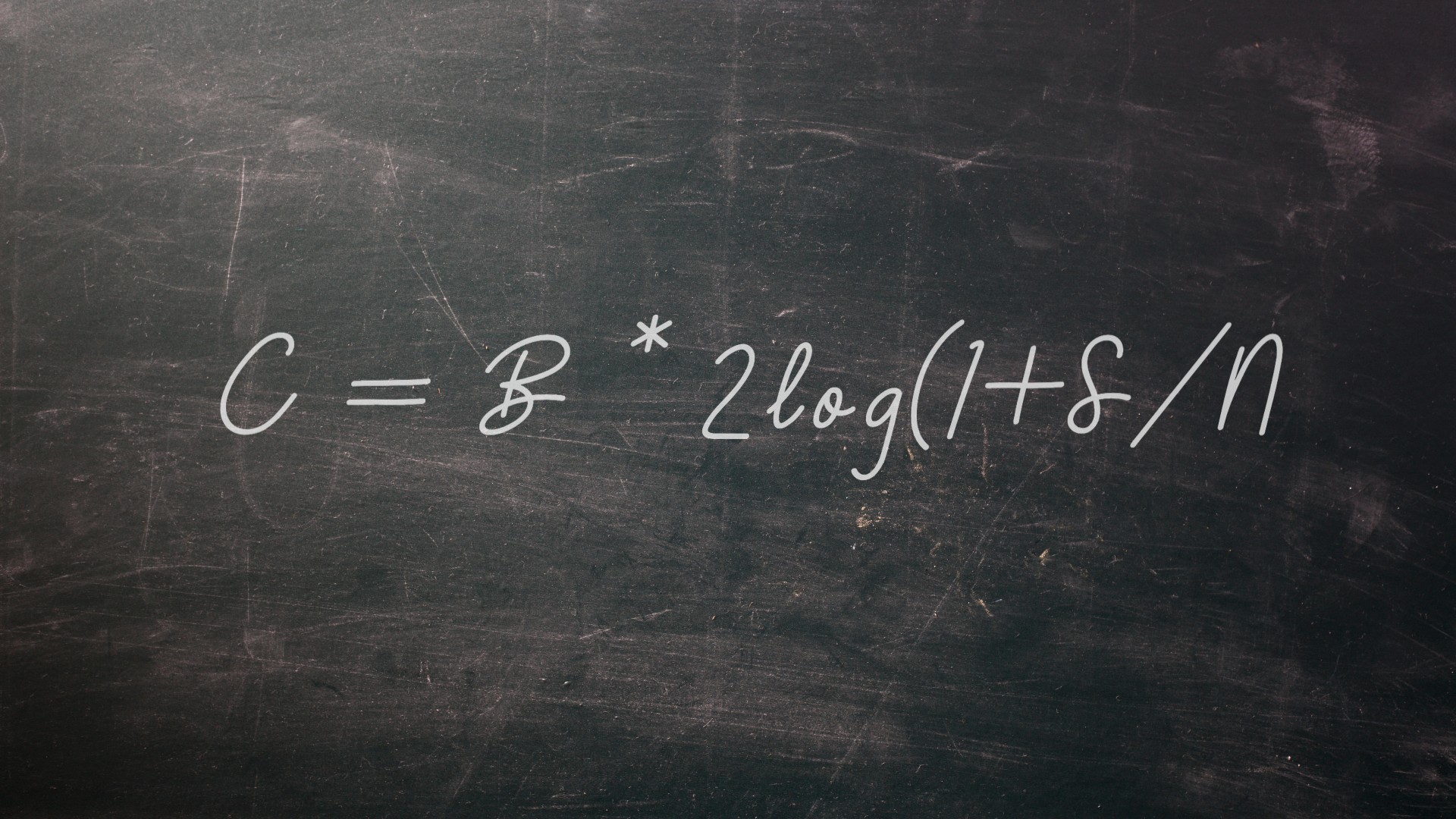
คนส่วนใหญ่คุ้นเคยกับ 0 และ 1s ที่ประกอบขึ้นเป็นบิตคอมพิวเตอร์ แต่แนวคิดที่สำคัญนี้จะไม่ได้รับความนิยมหากปราศจากงานบุกเบิกของนักคณิตศาสตร์ชาวอเมริกันและวิศวกร Claude Shannon ในกระดาษที่สำคัญในปี 1948 แชนนอนได้วางสมการที่แสดงประสิทธิภาพสูงสุดที่สามารถส่งข้อมูลได้ซึ่งมักจะได้รับเป็น c = b * 2log (1+s/n) ในสูตร C คือความสามารถที่ทำได้ของช่องข้อมูลเฉพาะ B คือแบนด์วิดท์ของเส้น S คือกำลังสัญญาณเฉลี่ยและ n คือกำลังเสียงเฉลี่ย (S มากกว่า N ให้อัตราส่วนสัญญาณต่อสัญญาณรบกวนที่มีชื่อเสียงของระบบ) ผลลัพธ์ของสมการอยู่ในหน่วยของบิตต่อวินาที ในปี 1948 กระดาษแชนนอนให้เครดิตความคิดของนักคณิตศาสตร์จอห์นดับเบิลยู. Tukey เป็นชวเลขสำหรับวลี“ เลขฐานสอง”
แผนที่โลจิสติกส์ของพฤษภาคม
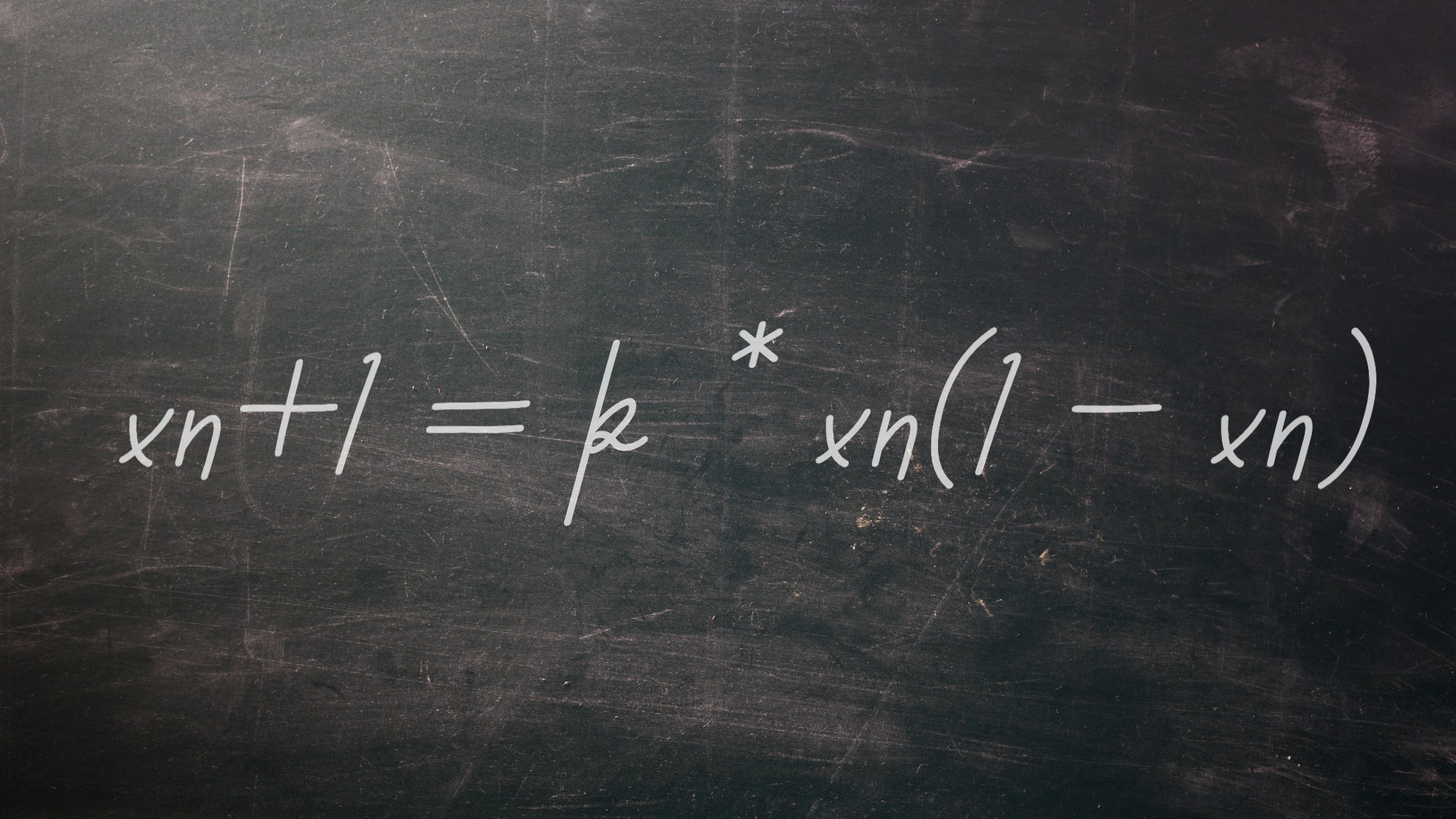
บางครั้งสิ่งที่ง่ายมากสามารถสร้างผลลัพธ์ที่ซับซ้อนอย่างไม่น่าเชื่อ ความจริงนี้อาจดูเหมือนไม่รุนแรงทั้งหมด แต่มันใช้เวลาจนถึงกลางศตวรรษที่ 20 สำหรับนักวิทยาศาสตร์ที่จะชื่นชมน้ำหนักของความคิดอย่างเต็มที่ เมื่อทฤษฎีความโกลาหลออกมาในช่วงเวลานั้นนักวิจัยเริ่มได้รับการจัดการกับวิธีการที่ระบบที่มีเพียงไม่กี่ส่วนที่เลี้ยงตัวเองอาจสร้างพฤติกรรมแบบสุ่มและคาดเดาไม่ได้ นักฟิสิกส์นักฟิสิกส์นักคณิตศาสตร์และนักนิเวศวิทยาโรเบิร์ตเมย์เขียนบทความที่ตีพิมพ์ในวารสารธรรมชาติในปี 1976 ชื่อ "แบบจำลองทางคณิตศาสตร์ที่เรียบง่ายที่มีพลวัตที่ซับซ้อนมาก" ซึ่งเป็นที่นิยมของสมการ xn+1 = k * xn (1 - xn)
XN แสดงปริมาณบางอย่างในระบบในเวลาปัจจุบันที่ดึงกลับมาเองผ่านส่วนที่กำหนดโดย (1 - xn) k เป็นค่าคงที่และ xn+1 แสดงระบบในเวลาต่อไปในเวลา แม้ว่าค่อนข้างตรงไปตรงมาค่าที่แตกต่างกันของ K จะให้ผลลัพธ์ที่แตกต่างกันอย่างดุเดือดรวมถึงบางอย่างที่มีพฤติกรรมที่ซับซ้อนและวุ่นวาย แผนที่ของพฤษภาคมถูกนำมาใช้เพื่ออธิบายการเปลี่ยนแปลงของประชากรในระบบนิเวศและสร้างตัวเลขสุ่มสำหรับการเขียนโปรแกรมคอมพิวเตอร์