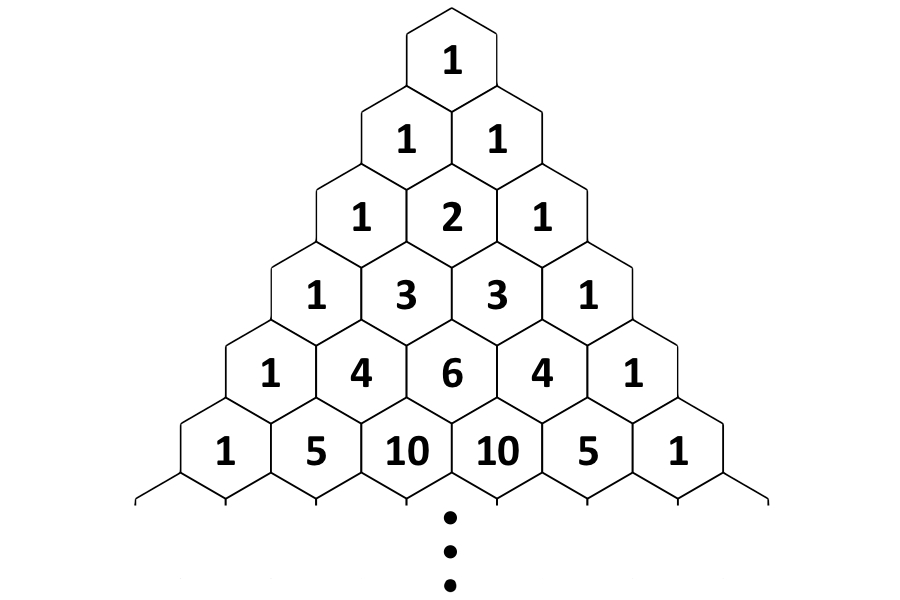
帕斯卡尔(Pascal)的三角形是一个永无止境的等值数字三角形,遵循以上两个数字以获取以下数字的规则。两个侧面是“全1”,因为三角形是无限的,所以没有“底部”。
它命名为Blaise Pascal这是一位17世纪的法国数学家,在概率理论的研究中使用了三角形。但是,它已经在世界范围内进行了数千年的研究,尤其是在古代印度和中世纪中国,在伊斯兰黄金时代和文艺复兴时期,始于意大利在遍布欧洲之前。
尽管这种模式很简单,但它在许多数学领域都具有令人惊讶的联系,包括代数,数字理论,概率,组合学(可计数配置的数学)和分形。在2013年现场科学的“专家声音”专栏中,纽卡斯尔大学学习的数学家迈克尔·罗斯(Michael Rose)描述了许多隐藏在帕斯卡(Pascal)三角形中的图案。在本文中,我们将专门研究高等数学中的属性。
组合
Pascal的三角形自然是通过对组合学的研究而产生的。例如,想象一下从五色标记中选择三种颜色。选择颜色的顺序对于选择在海报上使用的颜色并不重要,但是它可以为爱丽丝,鲍勃和颂歌选择一种颜色。可能的配置数量表示并计算如下:
- 爱丽丝,鲍勃和卡罗尔每种颜色:这种情况做物质称为排列。对于具有五个选项的情况,将选择三个选项并订购三个选项,此可能的排列表示为5P3,计算为5!/(5-3)!。操作员“!”称为阶乘,这意味着将所有较小的整数乘以一个较小的整数(例如5!= 5×4×3×2×1)5P3的表达式简化为5!/2! = 5×4×3 = 60
- 单个海报的三种颜色:这样的情况没有物质称为组合。可能的组合数量始终是可能排列数量的一小部分。对于将选择三个选项的情况,这将表示为5C3,并计算为5!/[3! (5-3)!] = 5! /(3!×2!)= 5×4×3 /(3×2×1)= 10
第二种情况对帕斯卡尔的三角形很重要,因为这些值可以按以下方式计算:
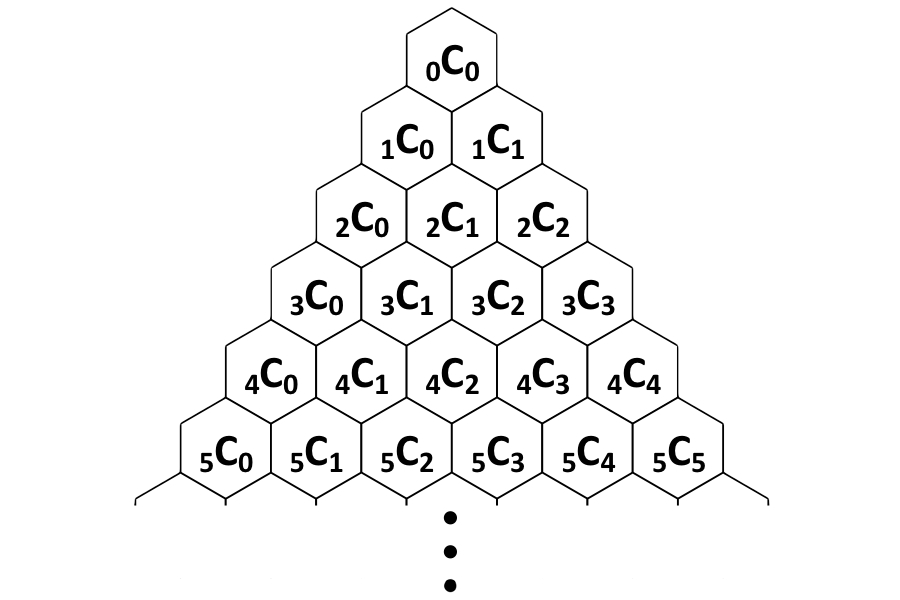
从生成Pascal的三角形的过程中,我们可以通过添加上面的两个数字来生成任何数字。从数学上来说,这表示为ncr=N-1cR-1+N-1cr- 在整个历史上,数学学者已经指出了这种关系。
二项式定理
二项式是代数中使用的单词,大致表示“添加两件事”。这二项式定理是指在二项式本身乘以一定数次时出现的系数(变量前出现的数字)的模式。从数学上讲,这写为(x + y)n。 Pascal的三角形可用于确定系数的扩展模式。前几个扩展的多项式如下。
使用求和表示法,二项式定理可以简洁地写为:
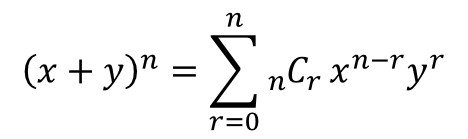
二项式分布
对于具有两个结果的概率过程(例如硬币翻转),结果的顺序由数学家和统计学家所说的结果支配二项式分布。这也与帕斯卡尔的三角形有关。
例如,对于三个硬币翻转,有2×2×2 = 8个可能的头部/尾部序列。当分为“多少头(3、2、1或0)”组时,每个组分别填充1、3、3和1序列。请注意,这与Pascal三角形的第三行是如何匹配的。它已经经过证明这种趋势适用于所有数量的硬币翻转和所有三角形的行。
根据乔治EP盒子的说法实验者的统计数据(Wiley,1978),对于大量的硬币翻转(大约20),二项式分布是合理的近似正态分布,一种基本的“钟形”分布,用作统计分析的基础。这种近似显着简化了大量现象的统计分析。
可以在豆机这是一种根据钉子的三角形排列方式随机将球随机分配给垃圾箱的设备。由于击中钉子的球具有同等的可能落到左或右的可能性,因此在传递一排一排的钉子后,球一直降落到左(或右)的可能性与同一币数量的所有头(或尾巴)的可能性完全匹配。在足够数量的球收集到三角形之后n钉行,每个垃圾桶中的球数比很可能与nTh帕斯卡的三角形行。
斐波那契序列
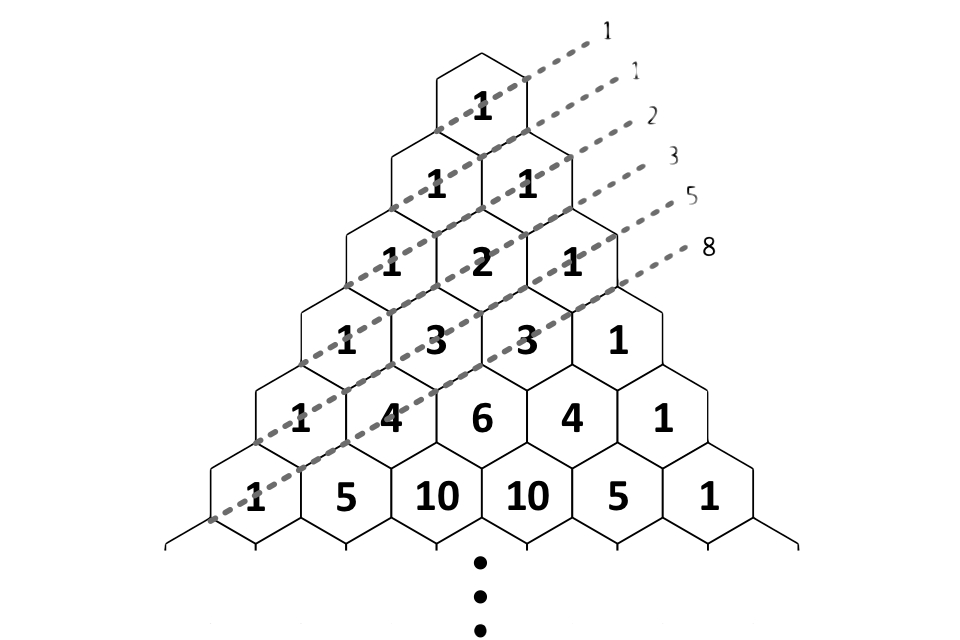
帕斯卡(Pascal)的三角形也与数字理论有很大的联系。最明显的连接是斐波那契序列。沿特定对角线添加帕斯卡尔三角形的数量会产生序列的数量。
分形
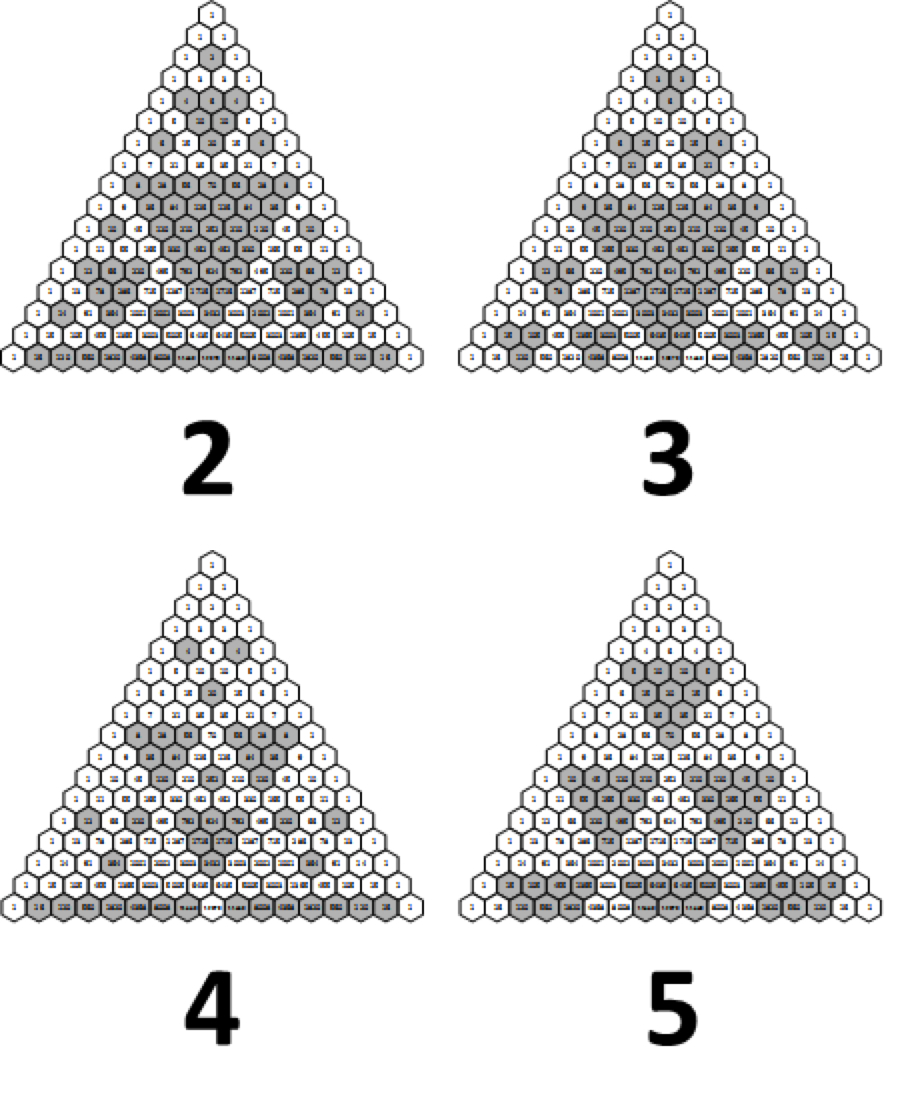
通过其可划分为帕斯卡尔三角形的数量着色会产生有趣的种类分形。特别是,将所有数字除以两个(所有偶数数字)都会产生Sierpin三角形。根据Wolfram MathWorld的说法,自13世纪以来,这些模式就出现在意大利艺术中。
其他资源
有关Pascal三角形的更多讨论,请转到: