最初是高中数学竞赛中的一个奖励问题,如今却产生了 10 种令人震惊的新方法来证明毕达哥拉斯定理的古老数学规则。
很长被认领不可能使用三角学来有效证明三角学基础定理。这落入逻辑谬误的循环思维试图用想法本身来证明一个想法。
“没有三角函数证明,因为三角函数的所有基本公式本身都是基于毕达哥拉斯定理的真理,”数学家 Elisha Loomis写过1927年。
但两位美国高中同学 Ne'Kiya Jackson 和 Calcea Johnson 在 2023 年高中最后一年实现了“不可能”。
现在他们已经公布了这些结果以及另外九个证明。
“有很多次我们都想放弃这个项目,但我们决定坚持完成我们开始的事情,”杰克逊和约翰逊在他们的论文中写下。

毕达哥拉斯定理描述了直角三角形三边之间的关系。
它对于工程和建筑非常有用,并被人类使用该方程归因于毕达哥拉斯,其中一些人认为,。
该定理是三角学领域的基本定律,本质上处理三角形的边和角之间的关系。您可能还记得方程 a2+b2=c2在学校里对你进行了钻研。
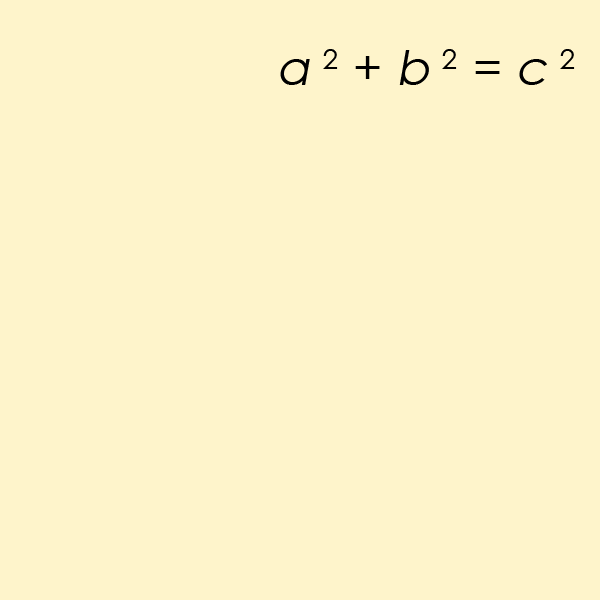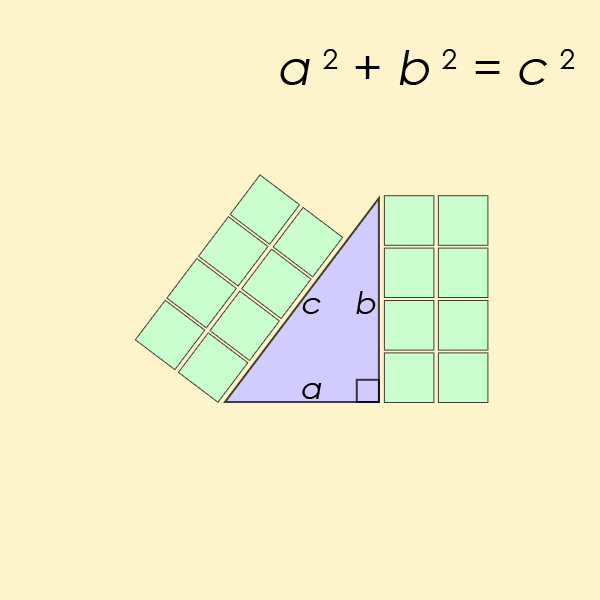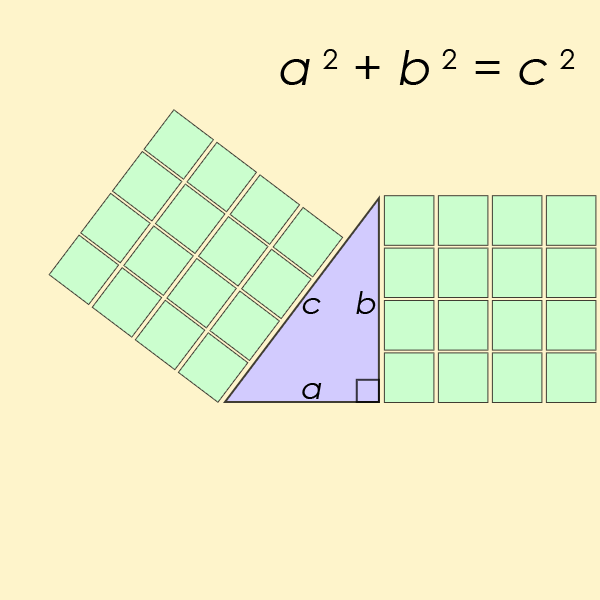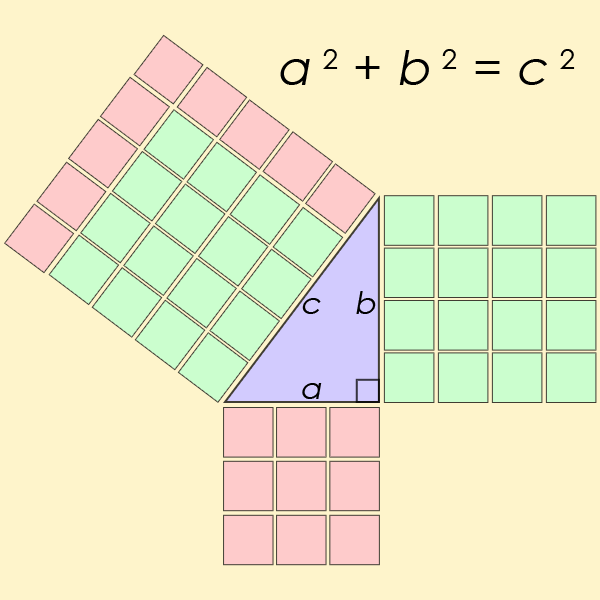
“学生可能没有意识到三角函数的两个相互竞争的版本已经被标记在相同的术语上,”解释杰克逊和约翰逊。
“在这种情况下,试图理解三角学就像试图理解两张不同图像打印在彼此之上的图片一样。”
通过解开这两个相关但不同的变体,杰克逊和约翰逊能够使用以下方法提出新颖的解决方案:正弦定理,回避直接的循环思维。
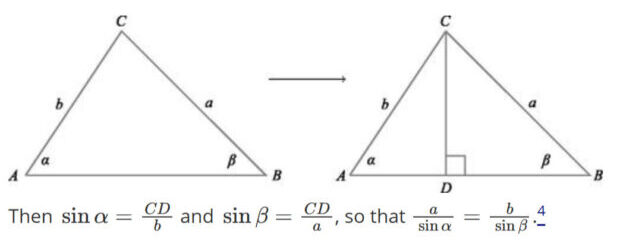
杰克逊和约翰逊在他们的新论文中概述了这种方法,尽管他们指出三角函数和非三角函数之间的界限有些主观。
他们还指出,根据他们的定义,另外两位经验丰富的数学家 J. Zimba 和 N. Luzia 也使用三角学证明了该定理,推翻了过去认为这是不可能的断言。
在他们的一个证明中,这两名学生将三角形计算的定义发挥到了极致,用一系列较小的三角形填充一个较大的三角形,并使用微积分求出原始三角形各边的测量值。
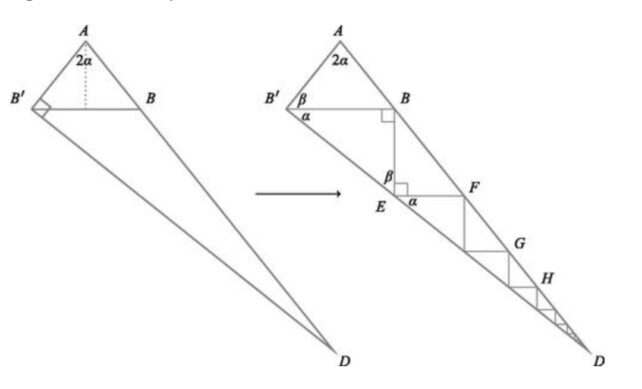
康涅狄格大学数学家阿尔瓦罗·洛扎诺-罗布莱多表示:“这看起来是我从未见过的”告诉科学新闻的 Nikk Ogasa。
杰克逊和约翰逊总共提供了一个关于两条边相等的直角三角形的证明,以及另外四个关于边不相等的直角三角形的证明,至少还剩下五个供“感兴趣的读者去发现”。
“这么年轻就发表论文,真是令人兴奋,”说约翰逊现在正在学习环境工程。杰克逊现在正在学习药剂学。
“他们的结果引起了人们对学生在该领域的新鲜视角的承诺的关注,”说德拉·邓博总编辑他们发表的期刊。
这项研究发表在美国数学月刊。