3月14日被庆祝为PI日,因为日期写为3/14时,与小数点扩展的开始3.14159相匹配……最著名的数学常数。
就本身而言,PI只是一个数字,在3到4之间的无数其他人中之一。使其著名的是它内置在您看到的每个圆圈中 - 周长等于Pi Times直径 - 更不用说本质上的其他一系列其他无关的环境,与钟形曲线分配到一般相对论。
庆祝PI日的真正原因是,数学纯粹是一个纯粹的抽象主题,它是如此很好地描述了我们的宇宙。我的书,数字的大爆炸,探索我们的现实数学有多难以连接。
也许最引人注目的证据来自数学常数:包括PI在内的罕见数字,通过在自然现象和相关方程式中出现如此频繁地(经常出乎意料的是出乎意料),以至于脱颖而出。像我这样的数学家以特殊的名称和符号来提高他们。
所以,还有什么数学常数值得庆祝吗?这是我开始填写其余日历的建议。
黄金比率
在一月份,我提名黄金比率,phi。如果将较大的数量除以较小的答案,则说两个数量在此比率中,与将两个数量的总和除以较大的数量相同。 PHI等于1.618…,由于没有1月61日,我们可以在1月6日庆祝。
首先由欧几里得计算,该比例由意大利数学家卢卡·帕里奥利(Luca Pacioli)推广,他写了1509年预订奢侈地赞美其美学特性。据说,莱昂纳多·达·芬奇(Leonardo da Vinci)为这本书画了60幅图纸将其纳入Mona Lisa功能的尺寸,选择一些主张是她的美丽负责。

phi自然界中的第一个暗示来自另一个意大利语斐波那契,而研究兔子如何繁殖。一个常见的生殖假设是,每对兔子每月都会再伴随着另一对。
从单个兔子对开始,然后连续的人口将遵循序列1、2、4、8、16、32、64、128、256之类的序列,也将乘以每月的“增长率”为2。
但是,斐波那契观察到的是,兔子花了第一个周期达到性成熟,然后才开始繁殖。一对现在给出了新的,较慢的进度1、1、2、3、5、8、13、21、34…。
这是著名序列以fibonacci的名字命名;请注意,每个人群都成为其两个前任的总和。
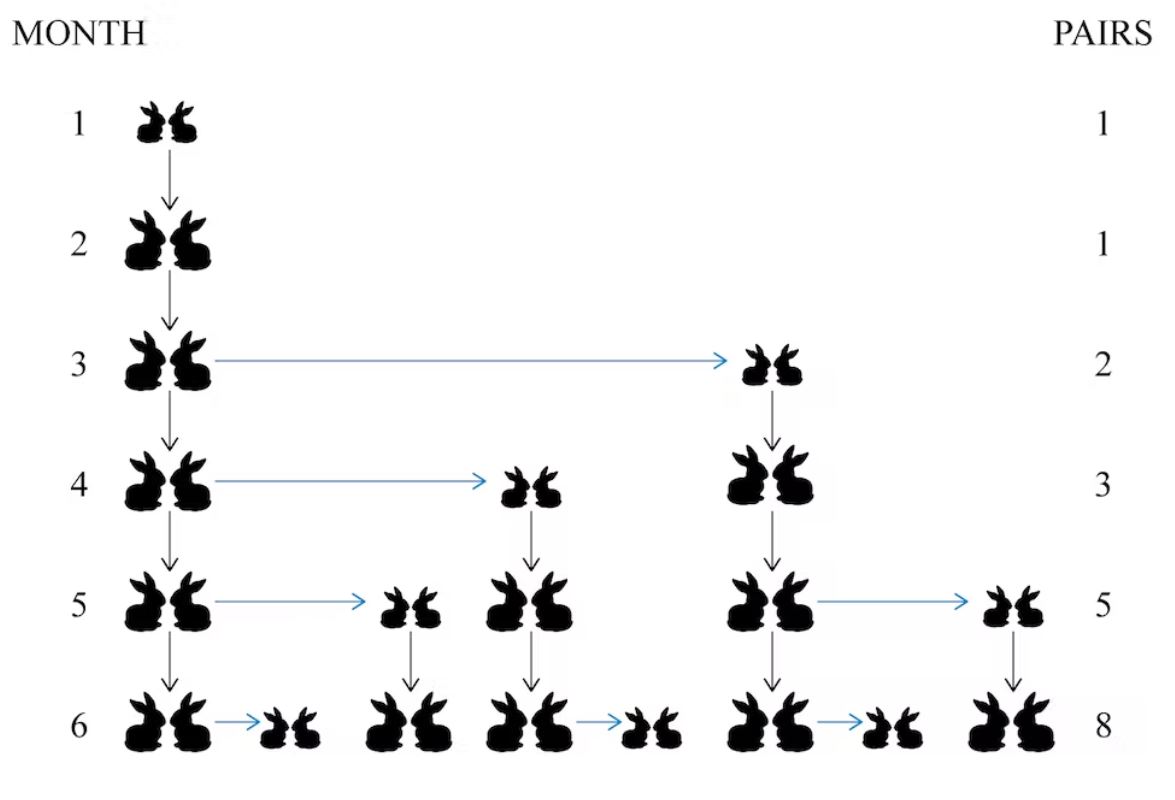
在所有这些兰迪兔子中,Phi如何显示?好吧,通过序列进行,您会发现每个数字大约是上一个数字的1.6倍。实际上,这种增长比率不断接近1.618…。
例如,21次约1.615倍13,而34次约1.619倍21。这意味着兔子定居下来以不再是2的生长比,而是越来越接近黄金比率。
实际的兔子不太可能准确地遵守此规则。首先,他们有不幸被掠食者食用的趋势。但是斐波那契数- 像5、8、13之类的 - 等等 - 大自然中广泛出现就像您可能在典型的松锥中看到的螺旋数一样。
是的,Phi本身也出现了几次,也许最著名的是叶子在茎上排列最大程度地接触阳光。
常数的“ e”
2月提供了另一个大片常数,欧拉的数字e,具有2.718…的值。因此,明年2月7日为Shindig马克。
要了解E,请考虑再次“加倍”增长,但现在就银行帐户中的“人口”而言。在某些奇迹上,您在此示例中的钱为您赚取了100%的利息,每年都会加重。年底,每笔投资1美元的投资将成为2美元。
但是,假设兴趣是半年复合的。然后,有50%的利息将记入中年,给您1.50美元。您在今年年底获得了$ 1.50的剩余50%的利息,该利息为0.75美元,为您提供2.25美元($ 1.50 + $ 0.75)。
因此,您的投资乘以2.25,而不是2。
如果银行之间的战争爆发,每种产品都将比较短和更频繁的间隔更加复杂100%的利息怎么办?就您的支出而言,天空会是极限吗?
答案是否定的。您可以将增长率从2个提高到约2.718 - 更确切地说是E-但是没有更高的地方。尽管您获得了更频繁的积分,但它们的回报逐渐减少。

在17世纪后期,发现微积分导致人们与宇宙斗争的能力取得了巨大的飞跃。现在,数学可以分析任何变化的东西 - 将其领域扩展到自然界的大多数现象。
常数E因其而出名在微积分中的标志性作用:事实证明,它是跟踪变化的最自然生长因素。因此,它出现在描述许多自然过程的法律中人口增长到放射性衰减。
当然,在我们的数学常数日历上的下一个PI将是三月。
我四月的提名人是Feigenbaum的恒定三角洲,等于4.669…,并衡量增长过程的速度旋转到混乱中。
我将等待我的第一批批次才能实现正式的假期状态,然后再进行任何候选人,很高兴考虑任何候选人你想提名。![]()
马尼尔·苏里(Manil Suri),数学和统计学教授,马里兰大学巴尔的摩县