在数学世界中,有两件事始终成立:首先,一些最顽固和最复杂的问题往往在现实世界中有着令人惊讶的应用;其次,对于那些实际上花费所有时间的人来说在在现实世界中,这些问题似乎……嗯,很傻。
以“沙发问题”为例:这个难题几十年来一直困扰着数学家,而且几乎所有搬过家的人都“解决”了这一难题。这是一个关于如何将弧形沙发移动到 90 度角的问题 - 是的,就像那一集一样朋友们你们现在都在引用。
移动的数学
从技术上来说,沙发的问题是这个:在宽度为 1 的走廊中,可围绕直角移动的最大面积区域是多少?最早被正式表述为1966年由奥地利裔加拿大数学家利奥·莫泽 (Leo Moser) 提出——尽管在此之前,这个问题多年来一直是围绕数学饮水机的讨论话题——但直到现在,还从未得到最终解决。
现在,您会注意到,此表述中没有提及同名长椅,实际上,作为解决方案建议的第一件“家具”实际上是一架“钢琴”。尽管如此,“沙发”这个术语很快就流行起来,主要是因为——好吧,看看它:
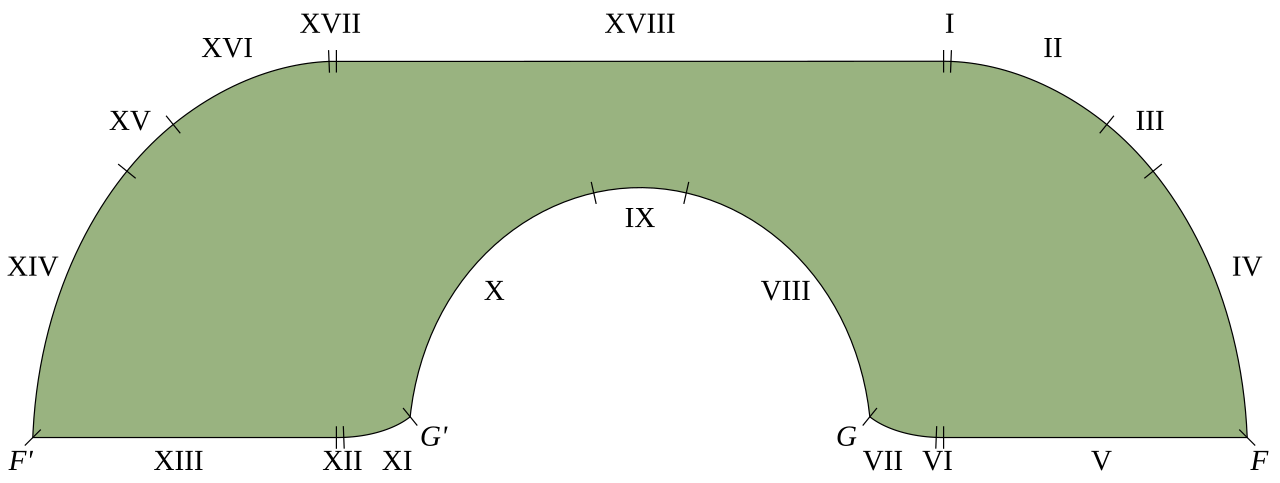
Gerver 沙发,显示了构成其边界的 18 个部分。
图片来源:TilmannR via维基共享资源,公共领域。
正是对下限的确定催生了标志性的沙发形状:在 1968 年的一篇论文中,我们没有骗你,论“现代数学”和学校和大学中类似的软知识垃圾对数学技能的削弱约翰·哈默斯利 (John Hammersley) 通过一些相对简单的微积分表明,该形状的面积为 (π/2) + (2/π) – 大约为 2.2074。
事实上,他走得更远。在同一篇论文中,他证明了该面积的上限由 2√2 给出——大约为 2.8284。虽然只过了几年,但沙发问题已经有了解决方案:确切的数字尚未确定,但数学家知道它必须在这两个值之间。找到真正的答案肯定不需要做更多的工作吗?
然而,25 年过去了,哈默斯利的弹跳仍然是我们最好的。直到罗格斯大学数学家 Joseph Gerver 站出来,提供了一张由 18 块材料制成的沙发分析上平滑连接的曲线部分。众所周知的“Gerver 沙发”将下限提高至 2.2195。
又过了四分之一个世纪,可能的解决方案的范围才会进一步缩小:2018年,数学家 Yoav Kallus 和 Dan Romik 使用计算机辅助证明将上限降低至 2.37。
这对哈默斯利最初的界限来说是一个很大的改进——但这个精确的解决方案仍然无法被捕获。
白克在比赛中
大约在卡勒斯和罗米克研究解决方案的同时,韩国首尔延世大学的博士后研究员 Jineon Baek 第一次开始思考沙发问题。现在,七年后,他认为他已经在尚未经过同行评审的证明中破解了这个问题。
“我为此投入了大量时间,但到目前为止还没有发表任何文章,”他告诉新科学家。 “现在我可以向世界说,我为这个问题做出了一些有价值的贡献,这一事实正在得到证实。”
对于一个如此容易陈述和想象的问题,白的证明并不是一件容易的事。它横跨 100 多页,它的作用远远不只是简单地暴力解决问题或不断地削减更小的区域。相反,罗米克告诉《新科学家》,这是一个“奇妙的发展”。
“我知道我永远不可能做到这一点,”罗米克说。 “我没有后悔的感觉,或者说,我怎么能错过这个,因为很明显,这不是我认为我能够想到的那种想法。 [Baek] 只是从一个完全不同的方向来解决这个问题。”
无需深入讨论细节,证明是这样的:首先,Baek 说,最佳沙发,无论结果是什么,都必须具有三个特定属性 - 它必须是单调的、平衡的,并且具有旋转角度π/2。同样,这些定义是相当技术性的,但本质上可以归结为:到目前为止我们使用的“沙发”已经几乎是正确的形状了。
其次,Baek 开始证明这张沙发如何移动到拐角处的条件——虽然是一件小事,但对于完成最后一步至关重要:定义这张沙发面积的上限,然后证明它等于 Gerver 的面积上限下限。
没错:32 年后,事实证明 Gerver 一直都是对的。
“我当然对这一切感到非常高兴,”格弗告诉《新科学家》。 “我已经75岁了,白不可能超过30岁。他比我有更多的精力、体力和存活的脑细胞,我很高兴他接过了接力棒。”我也很高兴我活得足够长,能够看到他完成我开始的事情。”
把脚抬起来
那么,沙发问题现在解决了吗?嗯,从技术上讲,这还有待观察。与所有数学证明一样,它需要经过同行评审以确保准确性——Baek 对此暗暗抱有希望。
“我不能说我百分百有信心,因为我们是人类,我们会犯错误,”他告诉新科学家。 “但是,我还是尽了最大努力让自己变得自信。”
但如果您自己解决沙发问题的希望因这个消息而破灭,请放心:既然 Baek 如此严格地定义了他的沙发,您随时可以为自己选择不同的形状。
当然,它可能不太适合你的客厅沙发,但你可能会说,没有什么能阻止你去……白去画板。
证据可以找到在 ArXiv 预印本服务器上。









