高中生發表的畢達哥拉斯定理「不可能」的證明

最初是高中數學競賽中的一個獎勵問題，但如今卻產生了 10 種令人震驚的新方法來證明畢達哥拉斯定理的古老數學規則。

很長被認領不可能用三角學來有效證明三角學基礎定理。這落入邏輯謬誤的循環思維試圖用想法本身來證明一個想法。

「沒有三角函數證明，因為三角函數的所有基本公式本身都是基於畢達哥拉斯定理的真理，」數學家 Elisha Loomis寫過1927年。

但兩位美國高中同學 Ne'Kiya Jackson 和 Calcea Johnson 在 2023 年高中最後一年實現了「不可能」。

現在他們已經公佈了這些結果以及另外九個證明。

「有很多次我們都想放棄這個項目，但我們決定堅持完成我們開始的事情，」傑克遜和約翰遜在他們的論文中寫下。

畢達哥拉斯定理描述了直角三角形三邊的關係。它對於工程和建築非常有用，並被人類使用該方程式歸因於畢達哥拉斯，其中一些人認為，。

此定理是三角學領域的基本定律，本質上是計算三角形的邊和角之間的關係。您可能還記得方程式 a²+b²=c²在學校裡對你進行了鑽研。

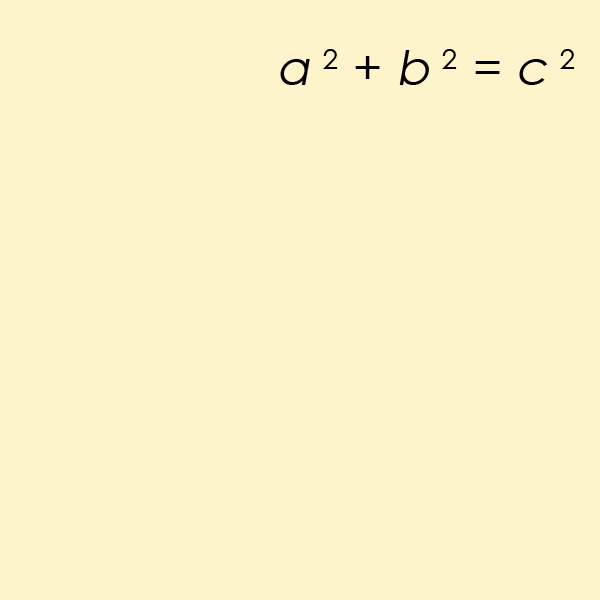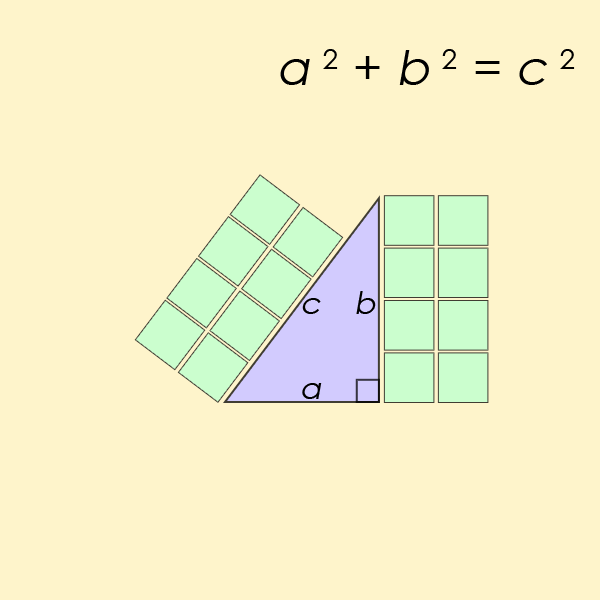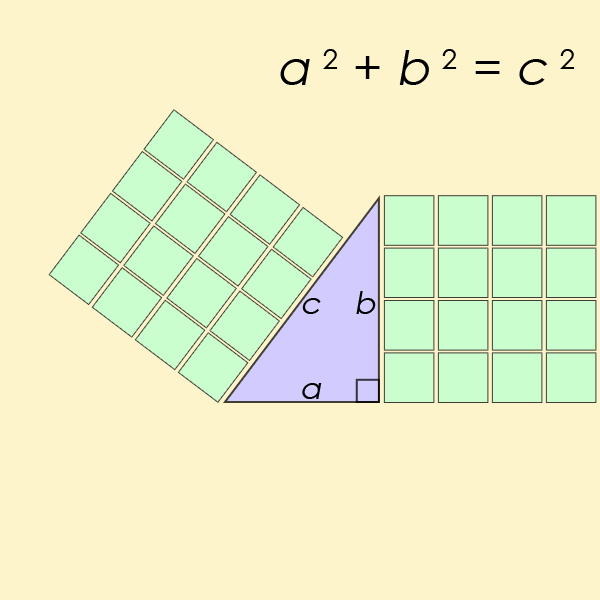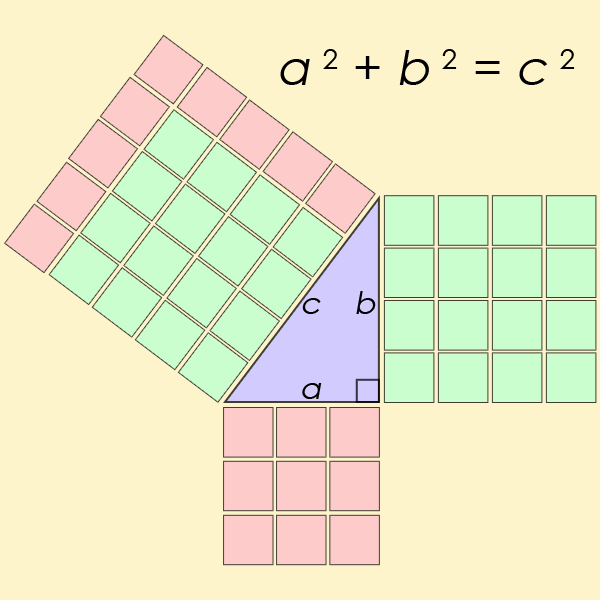
“學生可能沒有意識到三角函數的兩個相互競爭的版本已經被標記在相同的術語上，”解釋傑克森和約翰遜。

“在這種情況下，試圖理解三角學就像試圖理解兩張不同圖像印在彼此之上的圖片一樣。”

透過解開這兩個相關但不同的變體，傑克遜和約翰遜能夠使用以下方法提出新穎的解決方案：正弦定理，迴避直接的循環思維。

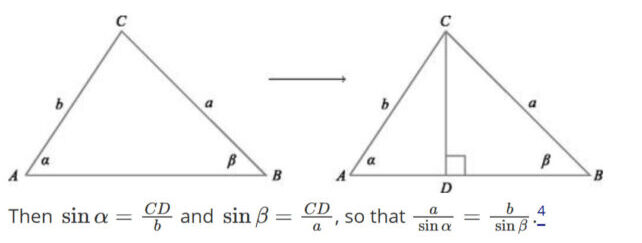
傑克遜和約翰遜在他們的新論文中概述了這種方法，儘管他們指出三角函數和非三角函數之間的界限有些主觀。

他們還指出，根據他們的定義，另外兩位經驗豐富的數學家 J. Zimba 和 N. Luzia 也使用三角學證明了該定理，推翻了過去認為這是不可能的斷言。

在他們的一份證明中，這兩位學生將三角形計算的定義發揮到了極致，用一系列較小的三角形填滿一個較大的三角形，並使用微積分求出原始三角形邊的測量值。

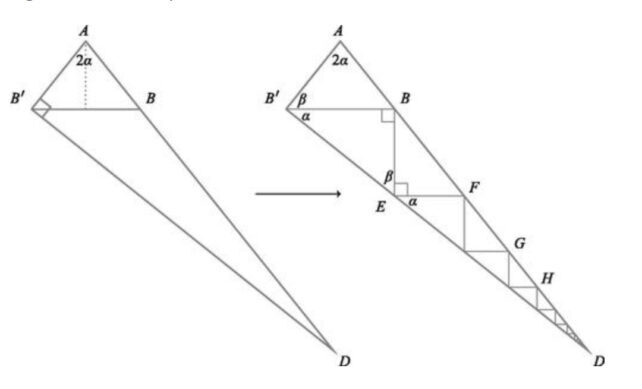
康乃狄克大學數學家阿爾瓦羅·洛薩諾-羅布萊多表示：“這看起來是我從未見過的”告訴科學新聞的 Nikk Ogasa。

傑克森和約翰遜總共提供了一個關於兩邊相等的直角三角形的證明，以及另外四個關於邊不相等的直角三角形的證明，至少還剩下五個供「有興趣的讀者去發現」。

“這麼年輕就發表論文，真是令人興奮，”說約翰遜現在正在學習環境工程。傑克遜現在正在學習藥劑學。

“他們的結果引起了人們對學生在該領域的新鮮視角的承諾的關注，”說德拉鄧博總編輯他們發表的期刊。

這項研究發表在美國數學月刊。