無聊嗎?

數學是唯一可以客觀地將其描述為“真實”的知識領域之一,因為其定理源自純邏輯。然而,與此同時,這些定理通常非常奇怪和違反直覺。
有些人發現數學無聊。如這些示例所示,這不僅僅是。
隨機模式
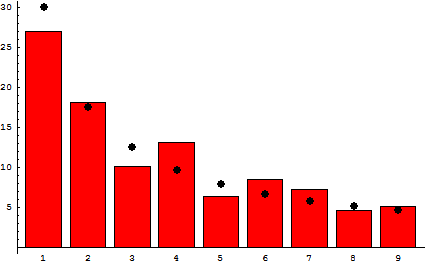
奇怪的是,隨機數據實際上並不是那麼隨機的。在給定的數字列表中,表示任何內容股票價格對於城市人口到建築物的高度到河流的長度,大約30%的人數將從數字1開始。較少的它們將從2開始,甚至較少,甚至以3個數字開始,依此類推,直到二十個中只有一個數字開始以9的速度開始。數據集越大,它跨越了它的跨度越大,它跨越了這種模式,就會出現這種模式。
主要的螺旋
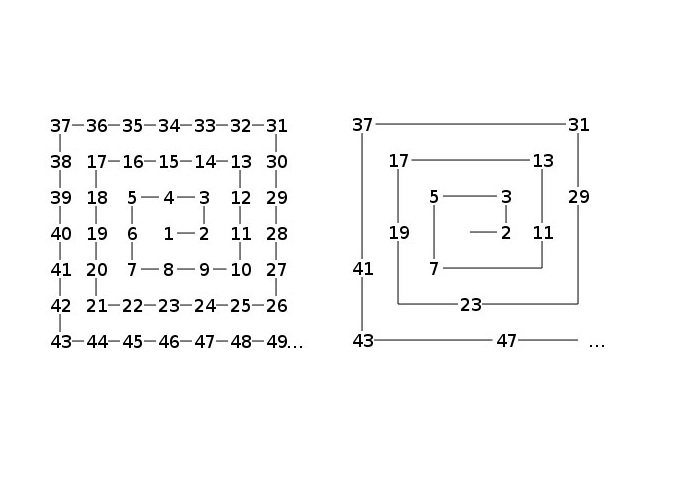
因為質數是不可分割的(除以1和他們自己),並且由於所有其他數字都可以寫成它們的倍數,因此它們通常被視為數學界的“原子”。儘管它們的重要性,但整數中質數的分佈仍然是一個謎。沒有模式決定哪些數字將是素數或連續的素數相距多遠。
素數的看似隨機性使“ Ulam螺旋”中的模式確實非常奇怪。
1963年,數學家Stanislaw Ulam在演示文稿中在筆記本上塗鴉時注意到了一個奇怪的模式:當整數以螺旋形式寫成時,質數似乎總是沿對角線掉落。這本身並不令人驚訝,因為除2號數字外,所有質數都是奇怪的,並且整數螺旋中的對角線交替奇怪,甚至是奇數。更令人震驚的是質數傾向的趨勢一些對角線比其他人更重要 - 無論您是從中間還是其他任何數字開始,都會發生這種情況。
即使您縮小更大的規模,如下數百個數字所示,您也會看到明確的尖角線線(黑點),有些線比其他線更強。關於為什麼出現這種主要模式的原因有數學猜想,但沒有得到證明。
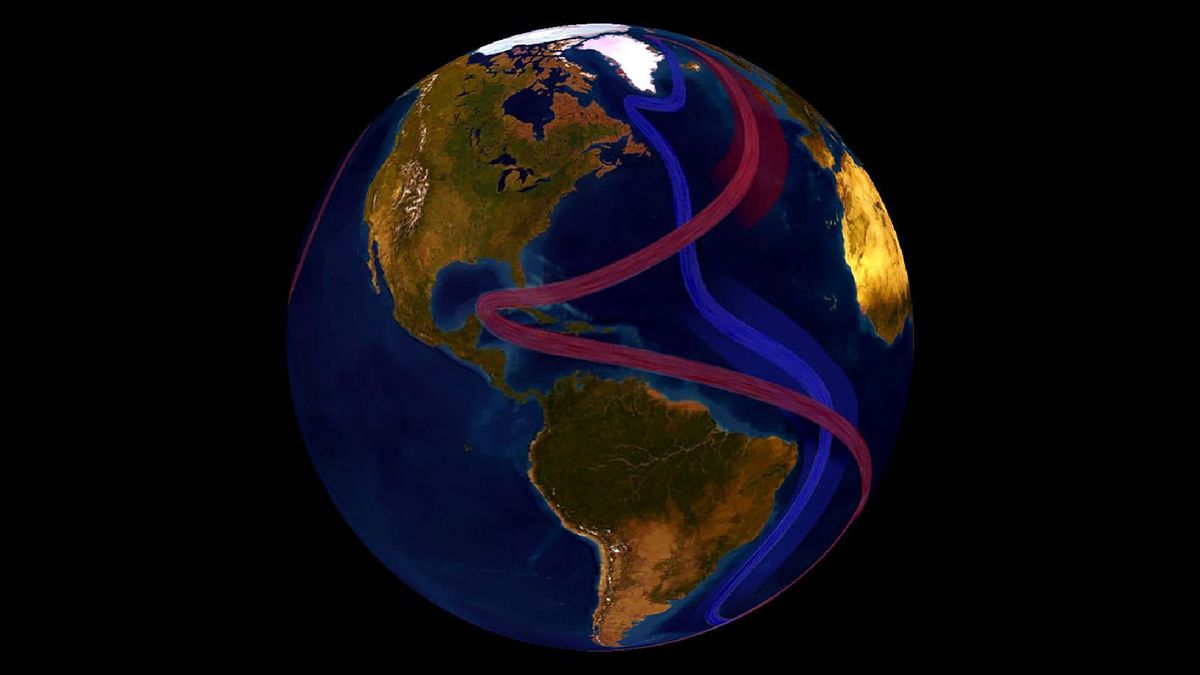
球體勢頭

{YouTube I6CGCA4MMCC&feature =相關}
在一個稱為拓撲的數學領域中,如果可以通過簡單地扭曲並伸展表面來將兩個對象視為等效或“同型”,則可以將兩個對像變成另一個對象。如果您必須切割或摺痕一個表面將其重塑為另一個形式,則它們會有所不同。
例如,考慮一個圓環 - 介紹幻燈片中顯示的dougnut形狀對象。如果您將其直立,將一側擴大並縮進該側的頂部,那麼您就有一個帶有手柄的圓柱體對象。因此,一個經典的數學笑話是說拓撲師無法從咖啡杯中告訴他們的甜甜圈。
另一方面,Moebius樂隊(其中有一個扭曲的循環)並非具有無扭曲的環(圓柱)的同構,因為您無法在不切割的一個邊緣上翻轉一個邊緣的Moebius頻段,然後翻轉一個邊緣。
拓撲家長期以來想知道:Sphere是同構具有自身的內而外版本嗎?換句話說,您可以向外旋轉一個球嗎?起初似乎是不可能的,因為您不允許在球體上戳一個洞並拉出內部。但實際上,“球形”所謂是可能的。觀看上面的視頻以查看如何完成。
令人難以置信的是,這裡顯示的複雜的球體方法的主要開發商Bernard Morin是盲目的。
牆數學

從數學上講,儘管它們可能以無限的繁榮裝飾,但只有有限的不同幾何圖案。所有的埃舍爾繪畫,壁紙,瓷磚設計以及所有二維形狀的重複排列都可以識別為屬於所謂的“壁紙組”中的一個或另一個。還有多少個牆紙組?正好17。 [計算器如何計算?這是給出的
十四行詩
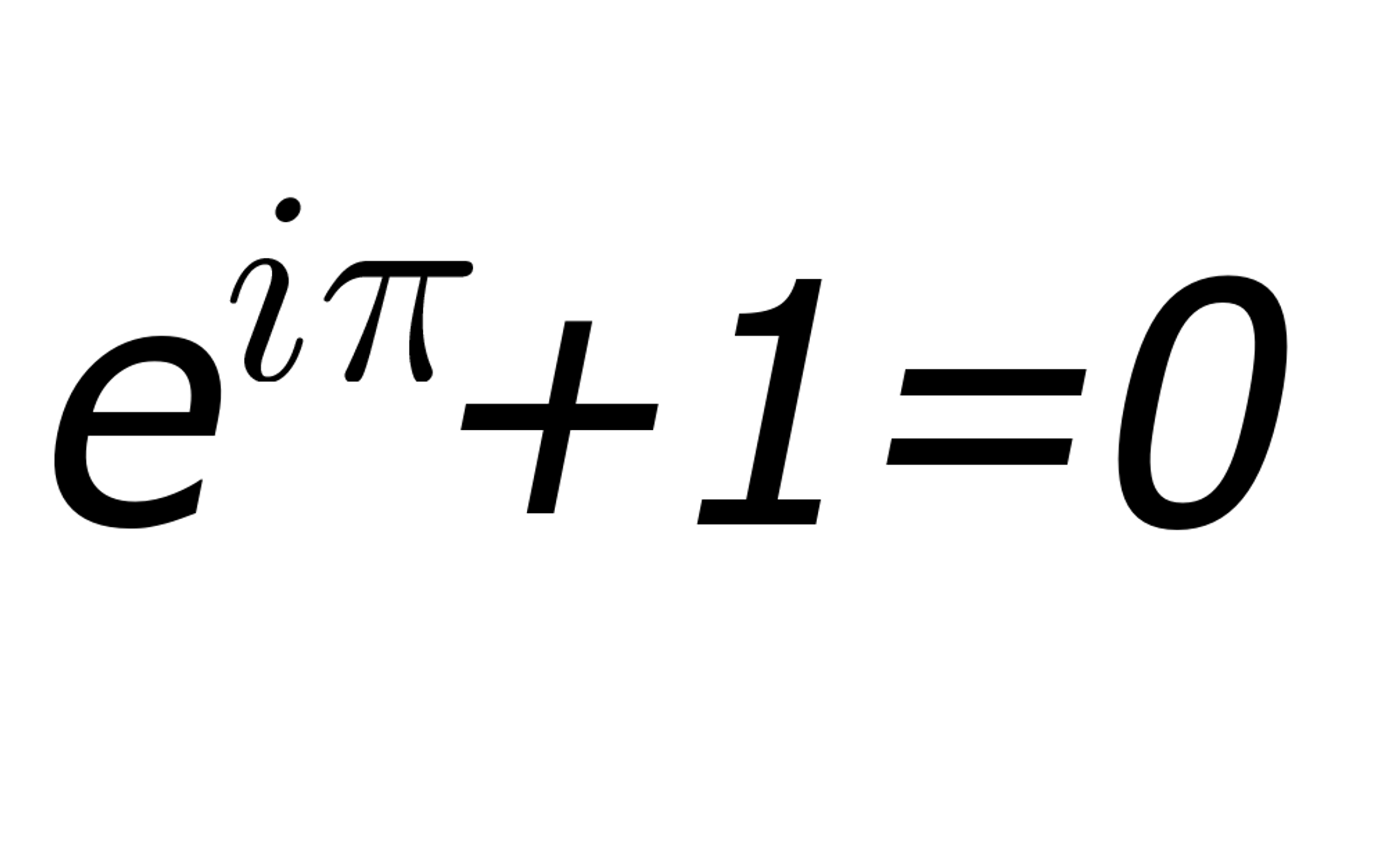
“就像莎士比亞的十四行詩一樣,它捕捉了愛的本質,或者是一幅繪畫,它帶出了人類形式的美麗,而不僅僅是皮膚深處,歐拉的方程式就陷入了生存的深處。”
斯坦福數學家基思·德文林(Keith Devlin)在2002年的文章中寫下了有關左派方程式的這些話,稱為“最美麗的方程式”。但是,為什麼歐拉的配方如此令人嘆為觀止?這是什麼意思?
首先,字母“ e”代表了一個不合理的數字(具有無休止的數字),開始於2.71828 ...在連續複雜的利益的背景下發現,它控制著指數增長的速率,從昆蟲種群到積累到放射性衰減。在數學中,該數字表現出一些非常令人驚訝的屬性,例如 - 使用數學術語 - 等於從0到無窮大的所有階乘的倒數總和。的確,不斷的“ E”遍及數學,在許多重要方程式中似乎都從無處出現。
接下來,“ i”代表所謂的“假想數”:負1的平方根。因此,它被稱為,因為實際上,沒有數字本身可以乘以產生負數(因此負數沒有真正的平方根)。但是在數學中,在許多情況下,有人被迫取下負面的平方根。因此,字母“ i”被用作標記完成此操作的地方的一種替身。
PI是圓的圓周與直徑的比率,是數學中最受歡迎,最有趣的數字之一。就像“ E”一樣,它似乎突然出現在大量的數學和物理公式中。是什麼讓Pi如此特別?這是給出的
將所有這些放在一起,升高的“ E”升高到虛構的“ I”的冪中,乘以Pi等於-1。而且,正如在Euler方程式中看到的那樣,將1添加給0。所有這些奇怪的數字(甚至不是真實的)幾乎是令人難以置信的。但這是一個經過證明事實。