做了一個團隊數學家只是朝回答160年曆史的數百萬美元的數學問題邁出了一大步?
或許。機組人員確實解決了一個稱為數字理論的領域中的許多其他較小的問題。這樣一來,他們重新開放了一條舊的途徑,最終可能會導致對舊問題的答案:是Riemann假設正確的?
雷曼假設是一種基本的數學猜想,對其餘數學具有巨大的影響。它構成了許多其他數學思想的基礎 - 但沒人知道它是否為真。它的有效性已成為最著名的公開問題在數學中。這是七個”千年問題“在2000年佈置,並承諾誰解決了他們將贏得100萬美元。 (此後僅解決了其中一個問題。)[5認真令人難以置信的數學事實這是給出的
這個想法從何而來?
早在1859年,一位名叫Bernhard Riemann的德國數學家提出了一個特別棘手的數學方程式的答案。他的假設是這樣的:riemann zeta函數的每個非平凡零的實際部分是1/2。那很漂亮抽像數學語句,必須與可以將哪些數字放入特定的數學函數中,以使該函數等於零。但事實證明,關於您遇到的頻率的問題,最重要的是素數當您朝著無限統計時。
稍後,我們將回到假設的細節。但是現在要知道的重要一件事是,如果Riemann假設是正確的,它將回答許多數學問題。
“在數量理論中,最終發生的事情通常是,如果您假設Riemann假設[是真的],那麼您就可以證明各種其他結果,”俄亥俄州Oberlin College的眾多理論家Lola Thompson沒有參與這項最新研究,他說。
她經常告訴現場科學,數字理論家首先會證明,如果Riemann假設是真的,則是真的。然後,他們將使用該證明作為一種墊腳石邁向更複雜的證據,這表明他們的最初結論是正確的,無論Riemann假設是否為真。
事實這個技巧她說,著作說服了許多數學家,黎曼假設必須是真實的。
但事實是沒有人確定。
朝著證明的一小步?
那麼,這個小型數學家團隊似乎是如何使我們更加靠近解決方案的呢?
埃默里大學(Emory University)的眾多理論家,新證明的合著者肯·奧諾(Ken Ono)說:“我們在論文中所做的事情是,我們重新審視了一個非常技術性的標準,該標準等同於Riemann假設……我們證明了其中的很大一部分。我們證明了這一標準的很大一部分。”
在這種情況下,“等同於Riemann假設的標準”是指數學上等同於Riemann假設的單獨陳述。
乍一看,這兩個陳述是如此連接,這並不明顯。 (標準與所謂的“詹森多項式的雙曲線”有關。)但是在1920年代,匈牙利數學家喬治·波利亞(GeorgePólya)證明,如果這個標準是真的,那麼Riemann假設是真實的 - 反之亦然。這是證明假設的一條古老的建議,但在很大程度上被放棄了。
Ono和他的同事在5月21日在《雜誌》上發表的一篇論文中自然科學院論文集(PNA)證明,在許多情況下,標準是正確的。
但是在數學中,許多人不足以算作證明。在某些情況下,他們不知道標準是對還是錯。
奧諾說:“這就像打一百萬個電球球。” “而且您知道所有數字,但最後20個數字。如果最後20個數字中的一個是錯誤的,那麼您就輸了。…它仍然可能崩潰。”
在所有情況下,研究人員都需要提出更高級的證明,以證明該標準都是正確的,從而證明了Riemann假設。 Ono說,目前尚不清楚這樣的證據有多遠。
那麼,這篇論文有多大的交易?
就Riemann假設而言,很難說這有多大。很大程度上取決於接下來會發生什麼。
湯普森說:“這個[標準]只是里曼假設的許多等效表述之一。”
換句話說,還有許多其他想法,例如這個標準,如果他們自己自己被證明了。
湯普森說:“因此,很難知道這是多少進展,因為一方面它在這個方向上取得了進展。但是,有很多等效的表述,也許這個方向不會產生Riemann假設。
如果證明沿著這條軌道出現,那麼這可能意味著Ono和他的同事開發了一個重要的基礎框架來解決Riemann假設。但是,如果它出現在其他地方,那麼本文將變得不太重要。
儘管如此,數學家仍然留下了深刻的印象。
“儘管這與證明Riemann假設相去甚遠,但這是一大步,”普林斯頓人數理論家Encrico Bombieri在5月23日的陪同下寫道。PNAS文章。 “毫無疑問,本文將激發其他數量理論以及數學物理學領域的進一步基本工作。”
(Bombieri贏得了田野勳章- 數學上最負盛名的獎項 - 1974年,在很大程度上是與Riemann假設有關的工作。 )
無論如何,Riemann假設是什麼意思?
我保證我們會回到這一點。這再次是Riemann假設:Riemann Zeta函數的每個非平凡零的實際部分是1/2。
讓我們根據湯普森(Thompson)和昂諾(Ono)解釋它的方式將其分解。
首先,Riemann Zeta功能是什麼?
在數學中,一個函數是不同數學數量之間的關係。一個簡單的看起來可能是這樣的:y = 2x。
Riemann Zeta函數遵循相同的基本原理。只有更複雜。這就是它的樣子。
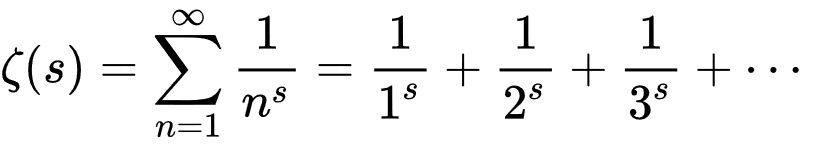
這是一個無限順序,每個術語 - 前幾個是1/1^s,1/2^s和1/3^s-添加到上一項中。這些橢圓形意味著該功能中的系列永遠繼續進行。
現在我們可以回答第二個問題:Riemann Zeta函數的零是什麼?
這很容易。該函數的“零”是您可以為X放入任何數字,這會導致函數等於零。
下一個問題:其中一個零的“真實部分”是什麼,它等於1/2是什麼意思?
Riemann Zeta功能涉及數學家所說的”複雜數字。 “一個複雜的數字看起來像這樣:a+b*i。
在該方程式中,“ A”和“ B”代表任何實際數字。實際數字可以是從負3到零到4.9234的任何東西,pi,約10億。但是還有另一種數字:假想的數字。當您取下負數的平方根時,會出現虛構數字,並且在各種數學環境中出現。 [關於PI的10個令人驚訝的事實這是給出的
最簡單的假想數是-1的平方根,其寫為“ i”。一個複雜的數字是一個實數(“ a”)加上另一個實數(“ b”)次i。複雜數字的“實際部分”是“ a”。
Riemann Zeta函數的一些零,即-10至0之間的負整數,不計入Reimann假設。這些被認為是“微不足道”的零,因為它們是實數,而不是複數。所有其他零是“非平凡”和復數。
Riemann假設指出,當Riemann Zeta函數交叉零(除-10和0之間的零以外)時,複數的實際部分必須等於1/2。
這個少的主張聽起來可能不是很重要。但這是。而且我們可能只是更接近解決它的十幾歲。
最初出版現場科學。