เป็นเวลาเกือบ 40 ปีแล้วที่สมมติฐานเล็กๆ น้อยๆ เรียบง่ายนั่งอยู่ในมุมหนึ่งของทฤษฎีกราฟอย่างเงียบๆ โดยคำนึงถึงธุรกิจของตัวเอง รู้จักกันในชื่อ "การคาดเดาแบบสองชั้น" ซึ่งดูเหมือนจะเป็นความจริงอยู่เสมอ แน่นอนว่าไม่มีใครสามารถทำได้พิสูจน์แต่มันก็สมเหตุสมผล และแน่นอนว่าไม่มีใครเคยพบตัวอย่างที่โต้แย้งมาก่อน
จนถึงตอนนี้. สร้างความประหลาดใจให้กับทุกคนนักคณิตศาสตร์กลุ่มหนึ่งได้ประกาศรายงานเมื่อเดือนที่แล้วว่าพวกเขาอ้างว่าพิสูจน์ได้ว่าการคาดเดานั้นเป็นเท็จ ปัจจุบันเผยแพร่บนเซิร์ฟเวอร์การพิมพ์ล่วงหน้าของ arXiv และดังนั้นจึงยังไม่ได้รับการตรวจสอบโดยผู้ทรงคุณวุฒิ บทความนี้จึงสร้างกระแสในโลกคณิตศาสตร์ ไม่เพียงแต่สำหรับการพิสูจน์เท่านั้น แต่ยังรวมถึงสิ่งที่กล่าวถึงเกี่ยวกับคณิตศาสตร์โดยรวมอีกด้วย
การคาดเดา
วางตำแหน่งครั้งแรกโดยนักฟิสิกส์ Pieter Kasteleynถึงเพื่อนร่วมงานในปี 1985การคาดเดาเรื่องเตียงสองชั้นไม่เกี่ยวอะไรกับเตียงเลย แต่มันเกี่ยวข้องกับกราฟ และเว้นแต่คุณจะเป็นนักคณิตศาสตร์ที่ทำงานอยู่ ก็อาจไม่ใช่กราฟแบบที่คุณกำลังคิดถึงอยู่ตอนนี้
“กราฟประกอบด้วยจุดยอดจำนวนหนึ่งและขอบอีกจำนวนหนึ่งที่เชื่อมต่อกับจุดยอด” Trefor Bazett ผู้ช่วยศาสตราจารย์สอนในภาควิชาคณิตศาสตร์และสถิติของมหาวิทยาลัยวิกตอเรียอธิบายวิดีโอ YouTube ล่าสุดเกี่ยวกับหลักฐาน
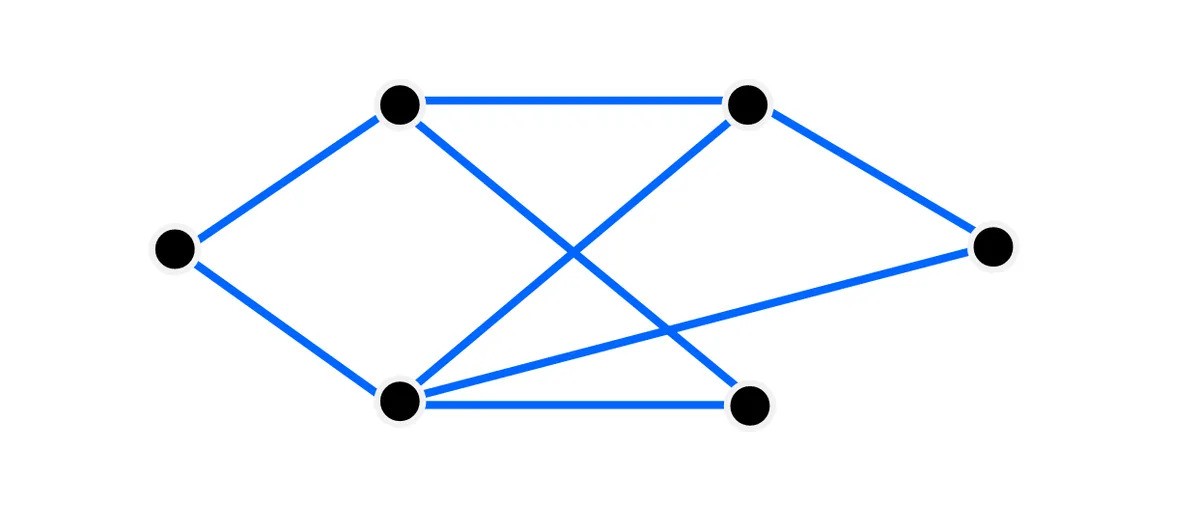
กราฟที่มีหกจุดยอดและแปดขอบ
เครดิตภาพ: IFLScience
“คุณสามารถจินตนาการได้ว่าบางที” เขาแนะนำ “แล้วความสัมพันธ์ก็คือว่าคุณเป็นเพื่อนกันหรือไม่”
เพิ่มกราฟนี้ให้ตรงกันเป็นสองเท่า และคุณสามารถสร้างสิ่งที่เรียกว่ากราฟสองชั้นได้ นั่นคือกราฟที่เหมือนกันสองกราฟวางซ้อนกันและเชื่อมต่อกันด้วย "โพสต์" ฟังนะ เมื่อคุณเห็นมันด้วยตัวเอง คุณจะเข้าใจคำศัพท์เฉพาะเรื่องทั้งหมด
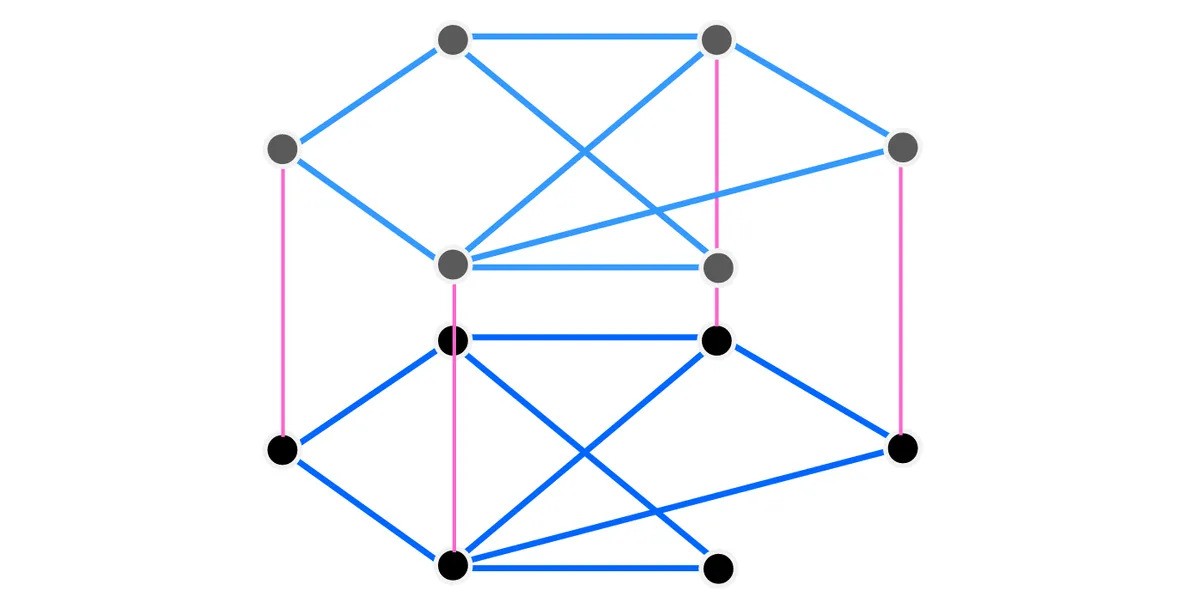
กราฟเดียวกันนี้วางในรูปแบบสองชั้น จุดยอดสีชมพูเหล่านั้นเรียกว่าเสาเตียง
เครดิตภาพ: IFLScience
ดังนั้นเราจึงจัดเตรียมไว้แล้ว ไม่ว่าจะเป็นมิตรภาพระหว่างผู้คน หรือสถานที่บนแผนที่ที่เชื่อมต่อกันด้วยถนน หรืออะไรก็ตามที่คุณจินตนาการถึงกราฟของคุณที่จะนำเสนอ ตอนนี้เราแค่จะคิดว่าจะเคลื่อนผ่านกราฟได้อย่างไร ดังนั้น สมมติว่าคุณต้องการได้จากจุดคุณเพื่อชี้โวลต์ในกราฟด้านบน เรามีตัวเลือกต่อไปนี้:
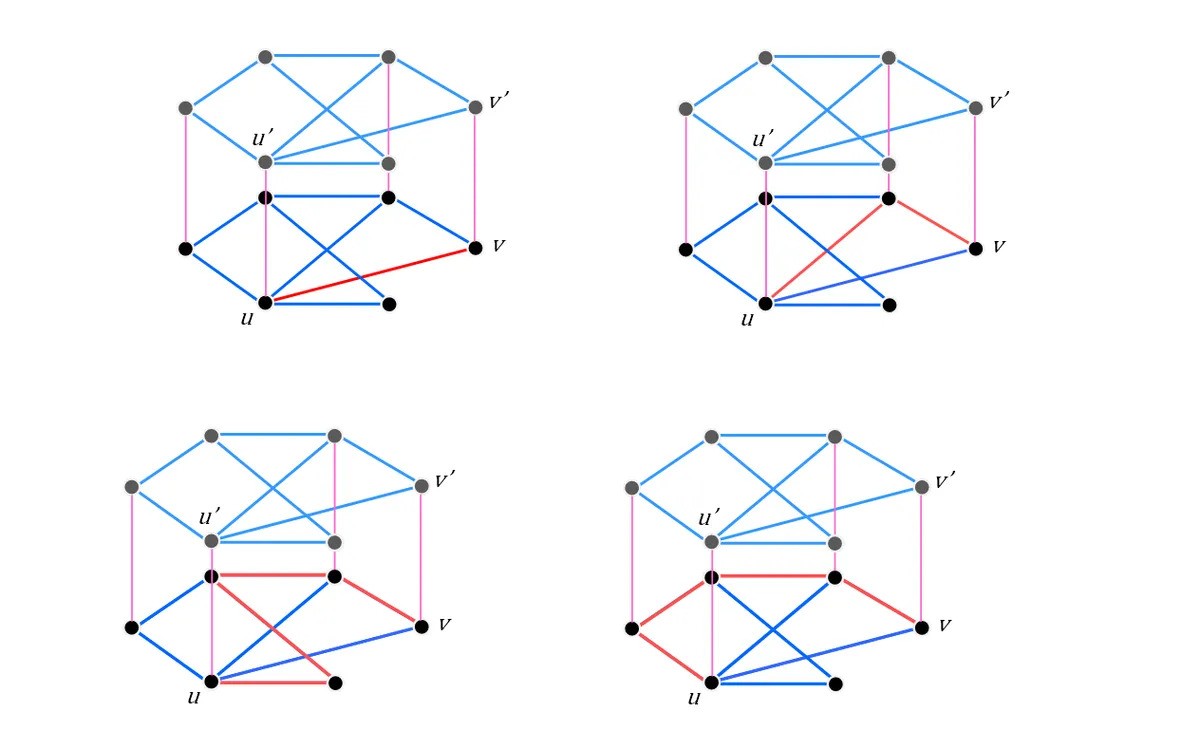
สี่เส้นทางที่มีศักยภาพ (ไม่หมดจด!) จากคุณถึงโวลต์เน้นด้วยสีแดง
เครดิตภาพ: IFLScience
กับเราจนถึงตอนนี้? เยี่ยมเลย เพราะนี่คือจุดที่สิ่งต่างๆ ซับซ้อนขึ้นเล็กน้อย สิ่งที่เราจะทำตอนนี้คือลบขอบบางส่วน – สูญเสียเพื่อน; ปิดกั้นถนน อะไรก็ได้ที่คุณต้องการ – และดูว่ามีโอกาสมากเพียงใดที่เรายังสามารถไปได้คุณถึงโวลต์หลังจากนั้น
ด้วยภูมิหลังทั้งหมดนั้น ตอนนี้เราจึงได้ทราบถึงคำกล่าวของการคาดเดาแบบสองชั้น ซึ่งก็คือ:ป-คุณโวลต์) ป-คุณวี'-
“มันบอกว่าความน่าจะเป็นที่ฉันจะได้รับจากคุณถึงโวลต์– นั่นคือ ความน่าจะเป็นที่ผมสามารถเคลื่อนที่ไปตามฐานได้ – มากกว่าหรือเท่ากับความน่าจะเป็นที่ผมจะเริ่มต้นจากฐานแล้วไปถึงวี'[…] บนเตียงชั้นบน” บาเซ็ตต์อธิบาย
“การคาดเดาบอกว่าสิ่งนี้เป็นจริงสำหรับกราฟที่เชื่อมต่อกันทั้งหมด และเซตย่อยของเสาเตียงทั้งหมด และทุกคู่คุณและโวลต์-
ตามสัญชาตญาณแล้ว มันสมเหตุสมผลแล้ว แน่นอนว่ามันจะง่ายกว่าที่จะไปถึงจุดสิ้นสุดในระดับเดียวกับจุดเริ่มต้นของคุณ มากกว่าจุดที่ต้องเดินทางขึ้นไปบนเสาเตียงด้วย การลองตัวอย่างเล็กๆ น้อยๆ จะช่วยเพิ่มความเชื่อมั่นนั้นได้ เว้นแต่ว่าคุณยินดีที่จะสร้างกราฟที่มีจุดยอดและขอบไม่กี่พันจุด
หลักฐาน
บ่อยครั้งในทางคณิตศาสตร์ การพิสูจน์สมมติฐานนั้นง่ายกว่าการพิสูจน์ หลังจากทั้งหมดเพื่อพิสูจน์บางสิ่งบางอย่าง คุณต้องแสดงให้เห็นว่ามันเป็นเรื่องจริงสำหรับทุกตัวอย่างที่เป็นไปได้ ในทุกสถานการณ์ – ถึงหักล้างคุณจะต้องค้นหาตัวอย่างแย้งเพียงตัวอย่างเดียวเท่านั้น
ปัญหาของการคาดเดาบนเตียงคือ ไม่มีใครมองหาตัวอย่างโต้แย้งนั้น “เหตุใดจึงต้องมองหาตัวอย่างแย้ง ในเมื่อการคาดเดานั้นเป็นความจริงอย่างเห็นได้ชัด” เขียนโดย Igor Pak ศาสตราจารย์คณิตศาสตร์ที่ UCLA และเป็นหนึ่งในผู้เขียนรายงานฉบับใหม่นี้ในโพสต์ในบล็อกเกี่ยวกับความก้าวหน้า
“ก็เพราะว่าคุณควรจะทำแบบนั้นเสมอ” เขาโต้กลับ “สำหรับการคาดเดาใดๆ โดยเฉพาะถ้าทุกคนเป็นเช่นนั้นแน่นอนเช่นเดียวกับในแน่ใจอย่างยิ่งโดยไม่ต้องสงสัยเลยว่าการคาดเดานั้นเป็นจริง”
ตอนนี้เป็นปี 2020; คุณรู้และพัคก็เช่นกัน “เราเริ่มต้นด้วยการทดลองคอมพิวเตอร์จำนวนมากมายโดยลองใช้กราฟเล็กๆ ทั้งหมด” เขาเขียน “เมื่อสิ่งเหล่านั้นล้มเหลว เราก็พยายามใช้ AI และเครื่องมือช่วยคอมพิวเตอร์อื่นๆ”
ถึงกระนั้น ดูเหมือนว่าจะไม่มีตัวอย่างโต้แย้งเกิดขึ้น และทีมงานเริ่มกังวลว่าถึงแม้จะมีคนปรากฏตัวขึ้น แต่ก็ไม่เพียงพอที่จะหักล้างการคาดเดาทั้งหมด กราฟที่ถูกสุ่มตัวอย่างโดยโครงข่ายประสาทเทียมมีขนาดใหญ่มาก ณ จุดนั้นซึ่งคำนวณความน่าจะเป็นที่เกี่ยวข้องอย่างแน่นอนคงเป็นไปไม่ได้ ดังนั้นการพิสูจน์ใดๆ ก็น่าจะถูกต้องอย่างแน่นอนถึง 99.9999 เปอร์เซ็นต์
แต่ในขณะที่ “ความเชื่อมั่น 99.99 เปอร์เซ็นต์ […] อาจเป็นมาตรฐานทองคำในฟิสิกส์นิวเคลียร์” พักเขียน “วารสารคณิตศาสตร์มักจะชอบความถูกต้อง 100 เปอร์เซ็นต์”
“วารสารส่วนใหญ่จะปฏิเสธแม้แต่น้อยพิจารณา'ห้าซิกมาตัวอย่างแย้ง” เขากล่าวเสริม
ดังนั้น แทนที่จะอดทนกับเทคนิคการเรียนรู้ของเครื่องที่ไม่ประสบผลสำเร็จ และผลลัพธ์อาจไม่ได้รับการยอมรับแม้ว่าจะประสบความสำเร็จก็ตาม ทีมกลับถอยกลับไปหนึ่งก้าว และแล้วในเดือนมิถุนายนปีนี้ กกระดาษกดปุ่ม arXiv ซึ่งเปลี่ยนแปลงทุกอย่าง
“ฉันพบมันในตอนเย็น และอ่านมันจนถึงตี 3” นิกิตา แกลดคอฟ หนึ่งในนักศึกษาระดับบัณฑิตศึกษาของ Pak และผู้ร่วมเขียนรายงานกล่าวควอนต้า- “ฉันก็แบบว่า 'ว้าว นี่มันบ้าไปแล้ว เหลือเชื่อจริงๆ'”
มันไม่ใช่ข้อพิสูจน์ของการคาดเดาบนเตียงอย่างแน่นอน แต่มันใกล้เคียง – เป็นการกำหนดข้อความที่เกี่ยวข้องกับวัตถุที่เรียกว่าไฮเปอร์กราฟ แทนที่จะเป็นกราฟ ผู้เขียนเป็นนักศึกษาปริญญาโทจากมหาวิทยาลัยเคมบริดจ์และนักกูเกิลที่ประสบความสำเร็จชื่อลอว์เรนซ์ ฮอลลอม ได้แสดงให้เห็นว่าในวัตถุเหล่านี้ การคาดเดาแบบสองชั้นนั้นเป็น... เท็จ
ฮอลลอมนำเสนองานของเขาเพื่อพยายามสรุปการคาดเดาแบบสองชั้น หรือปรากฏว่า ปรากฏว่าไม่สามารถสรุปได้ทั่วไป อย่างไรก็ตาม ในท้ายที่สุด บทความของเขาจะเป็นแรงบันดาลใจในการพิสูจน์การคาดเดาดั้งเดิม
ด้วยการแปลงไฮเปอร์กราฟของฮอลลอม ทีมงานได้สร้างกราฟที่อาจหักล้างการคาดเดาบนเตียงได้ มันช่างน่ากลัวอย่างยิ่ง โดยมีจุดยอด 7,222 จุด เชื่อมต่อกันด้วยขอบ 14,442 เส้น และความแตกต่างในความน่าจะเป็นที่เกี่ยวข้องนั้นมีเพียงเล็กน้อยเท่านั้น: “มีขนาดเล็กทางดาราศาสตร์” ปักเขียน “ตามลำดับที่ -10-6500-
“แต่มันเป็นลบ ซึ่งก็คือทั้งหมดที่เราต้องการ” เขากล่าวเสริม การคาดเดานี้เป็นเท็จอย่างเป็นทางการ
ผลพวง
แล้วนี่หมายความว่าอะไร นอกเหนือจากที่ชัดเจน? มีความผิดหวังอยู่บ้าง โดยเฉพาะอย่างยิ่งสำหรับนักคณิตศาสตร์และนักฟิสิกส์ประยุกต์ หากการคาดเดาแบบสองชั้นกลายเป็นจริง มันจะตรวจสอบสมมติฐานที่เชื่อกันอย่างกว้างขวางว่าของเหลวเดินทางผ่านของแข็งได้อย่างไร และให้ความร่วมมือกับนักวิจัยที่กำลังตรวจสอบฟิสิกส์ของการซึมผ่าน .
แต่ยิ่งไปกว่านั้น ยังมีผลกระทบทางศีลธรรมจากความก้าวหน้าอีกด้วย นักคณิตศาสตร์ในอนาคตควรจะเต็มใจยอมรับการพิสูจน์ความน่าจะเป็นมากกว่านี้หรือไม่? พวกเขาจะถูกต้องหรือสมบูรณ์หรือไม่?
“มันเป็นคำถามเชิงปรัชญา” Noga Alon ศาสตราจารย์คณิตศาสตร์ที่ Princeton กล่าวกับ Quanta “เราจะดูข้อพิสูจน์ที่เป็นจริงแต่มีความน่าจะเป็นสูงได้อย่างไร”
“บางทีการพิสูจน์ความน่าจะเป็นอาจทำให้คุณเข้าใจหรือสัญชาตญาณน้อยลงเกี่ยวกับสิ่งที่เกิดขึ้นจริง” เขากล่าว
สุดท้ายนี้ เป็นการเตือนนักคณิตศาสตร์ว่าอย่ายอมรับการคาดเดาเพียงเพราะพวกเขาชอบ “เราจะต้องสงสัย แม้แต่กับสิ่งที่โดยสัญชาตญาณดูเหมือนว่าจะเป็นจริง” อลอนกล่าว
เป็นความรู้สึกที่ภาคย์สนับสนุนมายาวนาน “การคาดเดาบางรายการได้รับแรงบันดาลใจจากเนื้อหาสาระ” เขากล่าวกับ Quanta “และการคาดเดาอื่นๆ ได้รับแรงบันดาลใจจากการคิดปรารถนา”
ดูเหมือนว่าการคาดเดาบนเตียงจะเป็นอย่างหลัง
บทความที่ยังไม่ได้ตรวจสอบโดยผู้ทรงคุณวุฒิสามารถดูได้ที่อาร์เอ็กซ์-









