在这个pi日，关于pi的12个令人惊讶的事实

事实：您可以使用PI来计算派的面积（前提是您知道零食的半径）。（图片来源：盖蒂图像）

当今，各地的数学书呆子都在挖掘一片馅饼，以庆祝其最具标志性的非理性数字：pi。毕竟，3月14日或3/14是纪念基本数学常数的最佳时机，其第一位数为3.14。

pi或π是圆的圆周与直径的比率。因为它是非理性的，所以不能将其写成一小部分。相反，它是一个无限长的，不重复的数字。

但是，如何发现这个非理性的数字，经过数千年的研究，这个数字仍然有任何秘密吗？从这个数字的古代起源到其模糊的未来，这里是关于PI的一些最令人惊讶的事实。

记住pi

PI计算为2,715个小数位。（图片来源：deymoshr/shutterstock）

印度韦洛尔的拉杰维尔·梅纳（Rajveer Meena）属于印度韦洛尔（Rajveer Meena）的记忆最多的记录。根据吉尼斯世界纪录。（截至2024年3月，Meena仍然保留此记录。）以前，Chao Lu，中国根据吉尼斯世界纪录，他在2005年将PI从记忆中朗诵至67,890个位置。

非官方的唱片持有人是Akira Haraguchi，他在2005年录制了他在100,000个小数位PI的朗诵录像中，最近又超过了117,000个小数位数，监护人报告。

数字爱好者已经记住了许多PI数字。许多人使用记忆辅助，例如被称为piphilology的助记解技术，以帮助他们记住。通常，他们使用用pilish写的诗（每个单词中的字母数量与PI的数字相对应）。说哪个...

有一个pi“语言”

文学书呆子发明了一种称为皮里什（Pilish）的方言，其中连续单词的字母数量与pi的数字匹配。例如，迈克·基思（Mike Keith）在皮里什（Pilish）中写下了《不唤醒》（Vinculum Press，2010）的书：

现在，我跌倒了，一个疲倦的郊区液体在树下，与欧洲暮色的森林旁边漂流。

（“现在”有三个字母，“我”有一个字母，“秋天”有四个字母，依此类推。）

指数增加

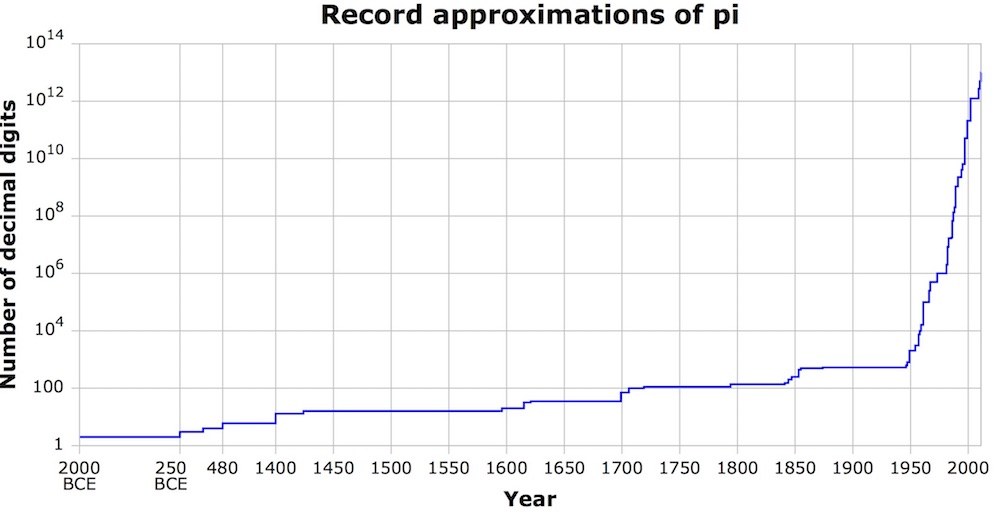
由于PI是一个无限的数字，因此，根据定义，人类将永远不会确定PI的每个数字。但是，自PI首次使用以来，计算出的小数位数的数量已成倍增长。巴比伦人认为这是公元前2000年的3 1/8足够好，而古代中国人和旧约的作家（国王7:23）似乎很高兴使用整数3。但是到1665年，先生，先生艾萨克·牛顿已将PI计算为16个小数点。到1719年，法国数学家托马斯·芬特·德拉格尼（Thomas Fantet de Lagny）计算了127个小数点，根据“ PI史”（St. Martin's Press，1976年）。

这计算机的出现从根本上提高了人类对PI的了解。根据“ PI的历史”（St. Martin's Press，1976年），在1949年至1967年之间，PI的已知小数从Eniac计算机上的2,037飙升至巴黎CDC 6600的500,000。

当然，最新的计算将这些早期记录从水中吹出。

PI有史以来最多的数字

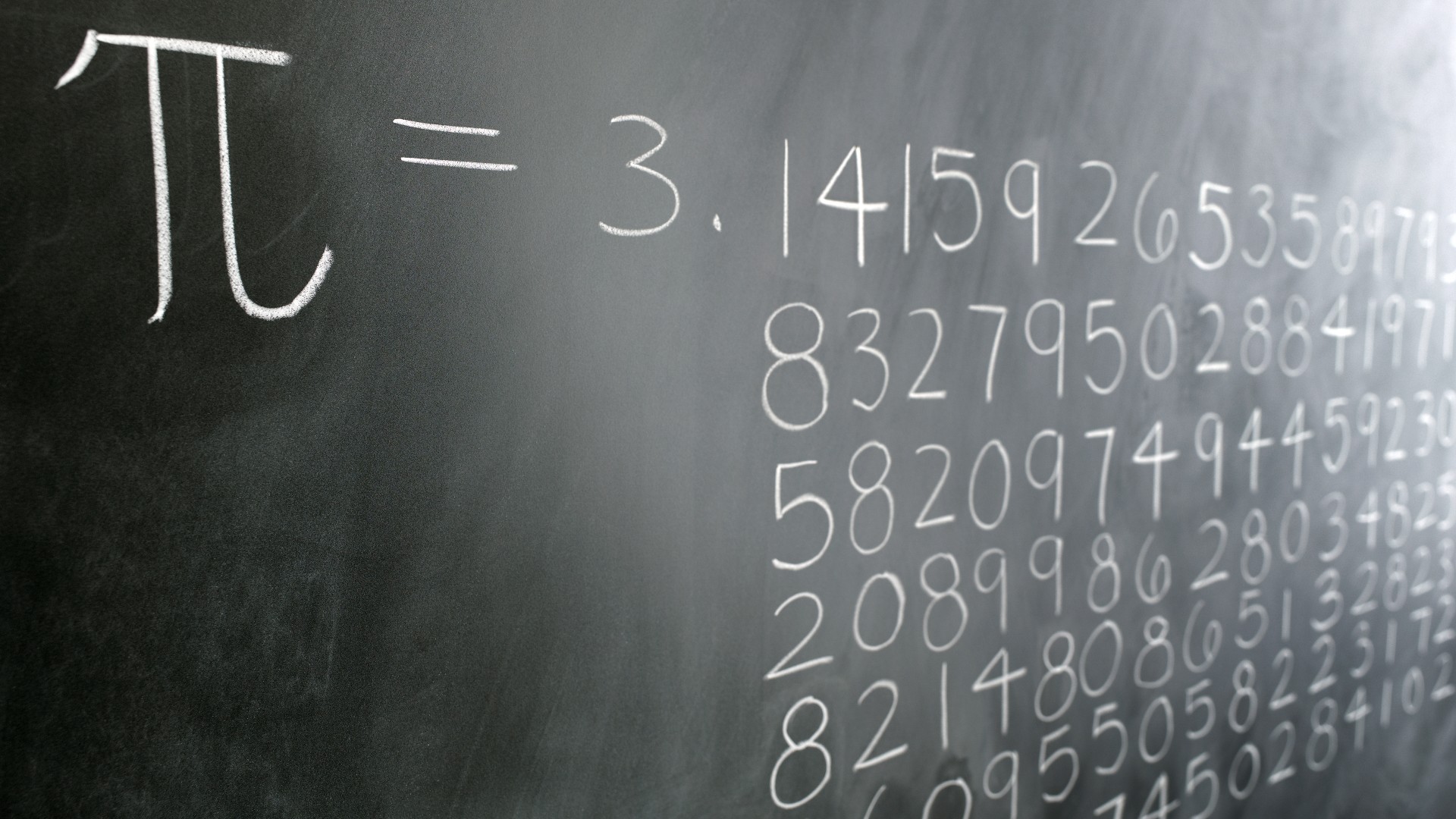
2021年，瑞士的研究人员使用超级计算机粉碎了现有的计算PI记录。

团队连续运行超级训练者108天计算为超过62.8万亿个小数的PI，将以前的计算记录吹到十二万亿个小数位。那是很多pi。

这种PI精度是前所未有的。但是，它可能会浪费在世界顶级科学机构之一上。

NASA仅使用16位PI数字

（图片来源：NASA AMES/JPL-CALTECH/T。PYLE，CHISTINE DANILOFF，麻省理工学院）

Pi的数字有多少位NASA需要对宇宙进行高精度计算吗？比您想象的要少。

据美国宇航局官员说，航天局很少需要使用超过16位PI（OR 3.141592653589793）对我们的太阳系及其宇宙社区进行准确的计算。根据NASA的数据，使用任何更长的PI版本都会显着减少回报。

例如：地球的直径约为7,900英里（12,700公里），这意味着其周长约为24,900英里（40,100公里）。根据NASA的说法，如果您要用PI的前16位数字和更准确的PI计算圆周，则具有数百个小数位的PI，这两个答案之间的差异将比人毛的宽度少300倍。

该机构补充说，在查看整个宇宙的规模时，PI的较大版本可能很有用。但是，随着我们太阳系中发生的大多数有趣的空间动作，NASA很少需要大于3.141592653589793。

手动ci

那些希望使用老式技术计算PI的人可以使用标尺，罐子和一根弦，量角器和铅笔来完成任务。罐方法的缺点是它需要一个实际圆形的罐子，并且精度受到一个人可以在其周围旋转的旋转状态的限制。同样，用量角器绘制一个圆，然后用尺子测量其直径或半径，涉及相当多的敏捷性和精度。

一个更精确的选择是使用几何形状。将一个圆圈分成多个细分市场（例如八个或10个披萨片）。然后，计算一条直线的长度，该直线将将切片变成一个同等长度的两个侧面三角形。所有侧面的加起来可产生PI的粗糙近似值。您创建的切片越多，PI的近似值就越准确。

发现Pi

（图片来源：Paul James Cowie/Wikimedia Commons）

这古老的巴比伦人知道Pi的存在将近4000年前。公元前1900年至公元前1680年的巴比伦平板电脑将PI计算为3.125，而著名的埃及数学文档1650年的Rhind数学纸莎草纸列出了3.1605的价值。国王詹姆斯圣经（i Kings 7:23）给出了cubit的pi近似，一个长度的古老单位，对应于前臂的长度从肘部到中指的尖端（估计约为18英寸或46厘米），根据威斯康星大学绿色湾。希腊数学家阿基米德（BC 287-212）使用The Pi近似Pi毕达哥拉斯定理，三角形侧面的长度与圆圈内外的多边形区域之间的几何关系。

Pi更名

（图片来源：Jakob Emanuel Handmann/Wikimedia Commons）

在将符号PI与圆形常数的关联之前，数学家不得不说一个人甚至可以描述数字。在旧数学书籍中发现的一个短语是拉丁语短语“ Quam cum Multiflicetur直径，Progeniet carrferencia中的Quantitas”，大致翻译为“当直径乘以其乘以其圆周时的数量，而该数量，产生圆周，”根据今天的历史。

当瑞士多头性变化时，非理性的数字升起莱昂哈德·欧拉（Leonhard Euler）1737年，他对三角学的驳斥使用了它。但是它并没有从欧拉（Euler）获得其pithier，希腊符号的名字。第一次提到PI是在一本鲜为人知的数学家威廉·琼斯（William Jones）的书中发生的，他在1706年在他的书《 Matholemiorum Matheseos》中使用了它。琼斯可能会使用PI的符号来表示圈子的外围，这是“ Pi的历史”（St. Martin's Press，1976年）。

PI正常吗？

PI绝对是奇怪的，但是正常吗？尽管数学家已经掩盖了这个非理性数字的许多奥秘，但仍然存在一些未解决的问题。

数学家仍然不知道PI是否属于所谓的正常数字的俱乐部，或数字中所有数字中具有相同频率的数字 - 这意味着每个时间为0到9，每次出现10％，根据Trueb的网站pi2e.ch。在2016年11月30日发表的论文中预印杂志Arxiv，TrueB计算出，至少基于前2.24万亿位数字，数字0到9的频率表明PI是正常的。当然，鉴于PI具有无限数量的数字，因此肯定会证明这一点的唯一方法是创建密封的数学证明。到目前为止，对这个最著名的非理性数字的证明已经避开了科学家，尽管他们在数字的属性和分布方面提出了一些范围。

pi听起来神圣

尽管科学家不知道PI是否正常，但他们对其其他特征有更好的了解。十八世纪的数学家约翰·海因里希·兰伯特（Johann Heinrich Lambert）通过使用持续的部分表达X的切线，证明了PI的非理性。

后来，数学家表明PI也是超验。在数学术语中，先验意味着该数字不能是任何具有合理数量系数的多项式的解决方案。换句话说，没有有限的根调格公式可以使用有理数来计算PI。

降级PI

尽管许多数学被PI迷上了，但仍有阻力运动。有人认为PI是一个派生的数量，而值TAU（等于PI的两倍）是一个更直观的非理性数字。

陶直接将圆周与半径联系起来，这是一个更具数学上的价值，迈克尔·哈特（Michael Hartl）是“ tau宣言”的作者，以前告诉现场科学。 tau在三角计算中也更好地工作，因此tau/4弧度对应于一个扫圈的角度，例如。

PI喜欢聚会

PI Day创始人拉里·肖（Larry Shaw）于2012年3月14日通过旧金山的探险家博物馆（Exploratorium Museum）带领游行者（每个人代表PI）。（图片来源：迈克尔·沃尔）

并不总是有PI天（当然，充满了馅饼）。 1988年，物理学家拉里·肖（Larry Shaw）在总部位于旧金山的探险家科学博物馆（Exploratorium Science Museum）推出了PI派对日。每年3月14日（3/14）的工作人员和访客每年走一场循环游行（是的，圆形的直径就像PI乘以其周长），每个人都拥有无限数量的PI。但是直到2009年，众议院通过了第224号决议，PI Day才成为全国性活动，”支持PI Day的名称“目标？对数学和科学的兴趣增加。让庆祝活动开始！

编者注：本文的较早版本于2024年3月14日更新，以包括新的更新和信息。现场科学撰稿人Tanya Lewis和编辑Brandon Specktor为本文做出了贡献。